Обработка биомедицинских сигналов: Учебное пособие, страница 13

Таблица 2. Принцип формирования первых восьми функций Уолша из        функций Радемахера.

4.3.2.2. Вычисление спектральных коэффициентов

Рассмотрим процесс вычисления спектральных коэффициентов на примере дискретизированного случайного входного сигнала (в частности, отсчетов ЭКС). Спектральные амплитуды А_i для i-й функции Уолша будут вычисляться по формуле

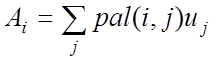                                          ,                                             (44)

где  j – номер временных отсчетов случайного сигнала и базисной функции  (при одинаковой частоте дискретизации);

u_j – амплитуда случайного сигнала в j-й момент времени.

Рассмотрим представление сигналов-примитивов в базисе функций Уолша.

Для постоянной составляющей m₀Uс₀ спектр сигнала будет состоять из одной спектральной амплитуды - А₀, представляющей собой нормированную сумму всех отсчетов сигнала. Все спектральные амплитуды более высокого номера обращаются в ноль в соответствии со свойствами самих базисных функций. Для всех функций Уолша, кроме pal₀, выполняется условие равенства нулю их интеграла за интервал времени, равный периоду функции. Для дискретных функций это соответствует равенству нулю суммы отсчетов базисной функции в течение периода. При вычислении спектральных амплитуд каждый из отсчетов базисной функции умножается на постоянный множитель а, что не влияет на итоговое равенство суммы нулю. Таким образом, спектр сигнала примет вид, как и в предыдущих рассмотренных случаях (рис. 26,а). Амплитуда спектральной составляющей А₀ численно равна коэффициенту m₀ .

Для линейно возрастающего сигнала m₁Uс₁ в спектре появляются только составляющие с номерами, кратными степени 2: А₁, А₂, А₄, А₈ и т.д. (рис. 26,б, в). Наличие в сигнале только линейной составляющей проявляется в спектре присутствием только определенных спектральных амплитуд, а именно соответствующих базисным функциям типа «меандр» Таким образом, наличие в спектре сигнала составляющих А₁, А₂, А₄, А₈ и равенство нулю всех остальных свидетельствуют о линейном характере сигнала. Условно назовем эти спектральные амплитуды «показателем монотонного изменения». Амплитуда этих составляющих прямо пропорциональна степени наклона прямой, описывающей сигнал, то есть коэффициенту m₁, а знак положителен при убывании и отрицателен при возрастании сигнала.

Для сигнала m₂Uс₂ в его спектре будут присутствовать только составляющие А₃, А₅, А₆, А₉, А₁₀, А₁₂… Эти составляющие можно условно назвать «показателями квадратичной нелинейности» (рис. 26,г, д).

Между значениями сигналов-примитивов и амплитудами спектральных составляющих существует определенная связь, которую можно охарактеризовать коэффициентом взаимосвязи.

а
б
в
г
д

Рис. 26.  Сигналы-примитивы и их спектральное представление в базисе функций Уолша

Пусть К_ij – коэффициент взаимосвязи между коэффициентом при i-м сигнале-примитиве и j-й спектральной составляющей. Первый индекс в обозначении коэффициента взаимосвязи характеризует степень, с которой время входит в функциональное описание сигнала-примитива.

Для вычисления К_ij воспользуемся свойством ортогональности базисных функций. Используем описание сигнала и функций в непрерывном относительном времени θÎ[0, Θ], где Θ=1 – период базисных функций. Представим сигнал в виде суммы его спектральных амплитуд, умноженных на соответствующую базисную функцию:

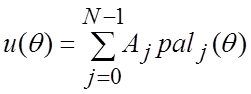.                                        (45)

Помножив обе части выражения (45) на pal_j(θ) и проинтегрировав в пределах [0,Θ], получим:

.

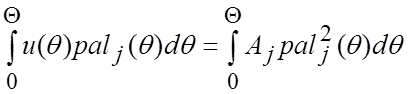Рассмотрим случай линейного сигнала: u(θ)= m₁Uс₁(θ).

С учетом свойств функций Уолша 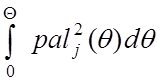=1 выражение для вычисления коэффициентов взаимосвязи К_1j примет следующий вид:

                     .             

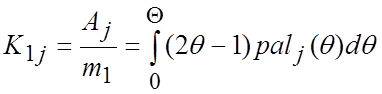Численные значения полученных коэффициентов взаимосвязи приведены в табл. 3.

Таблица 3. Коэффициенты взаимосвязи К_1j между m₁ и А_j

j	1	2	4	8
К1j	-1/2	-1/4	-1/8	-1/16

Таким образом, установив по характеру спектра принадлежность сигнала к классу линейных зависимостей, по амплитуде любой из спектральных составляющих А₁, А₂, А₄, А₈…  или по их совокупности можно установить значение коэффициента m₁, то есть определить степень и направление наклона.

Наличие в спектре сигнала составляющих А₃, А₅, А₆, А₉, А₁₀, А₁₂  указывает на то, что в его форме присутствует элемент нелинейности. При преобладании вогнутости в форме сигнала перечисленные спектральные амплитуды – положительны (рис. 26,г), при преобладании выпуклости – отрицательны (рис. 26,д). Для вычисления коэффициентов взаимосвязи К_2j между коэффициентом m₂ и j-й спектральной амплитудой можно использовать рассмотренную выше процедуру. Зная априори, что исследуемый сигнал может быть описан полиномом не выше второй степени, на основе значения какой-либо из перечисленных спектральных амплитуд может быть непосредственно вычислен коэффициент m₂:

,

,

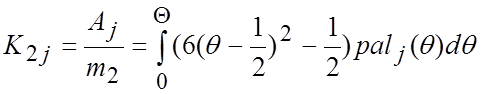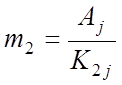где j=3,5,6,9,10,12…

Численные значения полученных коэффициентов взаимосвязи приведены в табл. 4.

Таблица 4. Коэффициенты взаимосвязи К_2j между m₂ и А_j

j	3	5	6	9
К2j	0.375	0.1875	0.094	0.094

Как видно из представленных графиков и соотношений, в базисе функций Уолша выполняется требование локализации. Выбрав в качестве информативных параметров составляющую А₀, одну из составляющих «монотонного изменения» и один из «показателей квадратичной нелинейности», можно сформулировать решающие правила для оценки основных параметров формы ST-сегмента. Очевидно, что в качестве спектральных амплитуд – информативных параметров наклона и выпуклости/вогнутости  предпочтительнее использовать составляющие, на которые приходится наибольшая часть энергии информативного сигнала, и самые простые в вычислительном отношении – А₁ и А₃ соответственно. 

4.3.2.3. Классификация типа формы

На основе вычисленных значений спектральных амплитуд в базисе функций Уолша А₀, А₁ и А₃ можно осуществить классификацию типов формы ST-сегмента на нормальные и характеризующие то или иное отклонение от нормы. Выделяют следующие коды формы [19]: FST=1—норма;