Моделирование полосковых линий: Учебное пособие

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

РЯЗАНСКАЯ ГОСУДАРСТВЕННАЯ РАДИОТЕХНИЧЕСКАЯ АКАДЕМИЯ

Е.П. ВАСИЛЬЕВ

МОДЕЛИРОВАНИЕ ПОЛОСКОВЫХ ЛИНИЙ

Рязань 2004

Министерство образования и науки Российской Федерации

Рязанская государственная радиотехническая академия

Е.П. ВАСИЛЬЕВ

МОДЕЛИРОВАНИЕ ПОЛОСКОВЫХ ЛИНИЙ

Учебное пособие

Рязань 2004

УДК 621.372.8

Моделирование полосковых линий: Учеб. пособие Е.П. Васильев; Рязан. гос. радиотехн. акад. Рязань, 2004. 48 с.

Рассматриваются методы анализа и синтеза полосковых линий. Приводятся выражения для расчета электрических и конструктивных параметров, на основе которых реализована программа автоматизированного проектирования различных типов полосковых линий передачи.

Предназначено для самостоятельной работы аспирантов и студентов, обучающихся по специальностям радиотехнического профиля.

Табл. 2. Ил. 11. Библиогр.: 14 назв.

Полосковая линия, параметры, автоматизированное проектирование

Печатается по решению редакционно-издательского совета Рязанской государственной радиотехнической академии.

Рецензент: кафедра технологии радиоаппаратуры Рязанской государственной радиотехнической академии  (зам. зав. кафедрой ТРЭА канд. техн. наук, доц. В.И. Рязанов)

Васильев Евгений Петрович

Моделирование полосковых линий

Редактор И.П. Перехрест

Корректор Е.В. Ипатова

Подписано в печать 15.10.04. Формат бумаги 60х84 1/16.

Бумага газетная. Печать трафаретная. Усл.печ. л. 3,0.

Уч.-изд. л. 3,0.    . Тираж 50 экз. Заказ 

Рязанская государственная радиотехническая академия.

390005, Рязань, ул.Гагарина, 59/1.

Редакционно-издательский центр РГРТА.

              ©      Рязанская государственная

радиотехническая академия, 2004

ВВЕДЕНИЕ

В диапазоне СВЧ используется большое количество разнообразных линий передачи (ЛП). К ним относятся полосковые, микрополосковые, щелевые, копланарные, связанные полосковые и связанные микрополосковые линии. Эти ЛП применяются наиболее часто. Полу-, четверть- и 1/8-волновые отрезки этих линий являются основными элементами большинства СВЧ устройств. ЛП характеризуются волновым сопротивлением и постоянной распространения, которые определяются конструктивными параметрами структуры и свойствами используемых диэлектрических и проводящих материалов.

Выбор конструктивных параметров и допусков на них - важная и сложная задача обеспечения качества микрополосковых СВЧ узлов. Очень важно исследовать чувствительность ЛП к изменению конструктивных параметров. С помощью анализа чувствительности, использующего частные производные, исследуются отклонения характеристик ЛП.

I.  МЕТОДЫ АНАЛИЗА И СИНТЕЗА

Общие соображения. В данной работе рассматриваются, в основном, методы анализа полосковых линий (ПЛ), использующие квази-Т приближение, при этом анализ сводится к решению двухмерного уравнения Лапласа с учетом граничных условий. В то же время для симметричной щелевой линии (СЩЛ) основной волной является волна, напоминающая конструкцию волны Н₀₁ в прямоугольном волноводе. В соответствии с задачами данного учебного пособия здесь приводятся некоторые приближенные соотношения, поясняющие, с одной стороны, физику работы СЩЛ, а с другой - пригодные для использования в системах автоматизированного проектирования.

Соотношения для симметричной полосковой (одиночной и связанных), микрополосковой (одиночной и связанных), СЩЛ и копланарного волновода (КВ) приведены из работы [1], а для четырехслойной ПЛ - на основе анализа статей [2-4]. Структура и интерфейс пакета прикладных программ (ППП) расчета параметров ПЛ ПОИСК-П приведены на основании работы [5]. При этом ППП объединяет единой интерфейсной оболочкой различные программы расчета ПЛ и позволяет обеспечить удобный и наглядный ввод и вывод информации в режиме анализа и синтеза.

1.1. Электрические параметры линий передачи

Произвольную длинную линию можно описать дифференциальными уравнениями [6] вида:

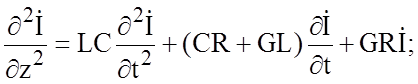                      (1.1)

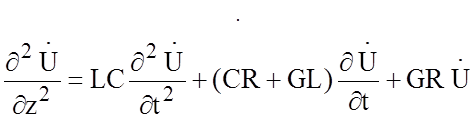              (1.2)

При этом напряжение U(z) вдоль линии изменяется так, как погонное сопротивление линии R обусловливает омическое падение напряжения, а погонная индуктивность L обусловливает индуктивное падение напряжения. Ток I(z) вдоль линии изменяется так, как одна часть тока в виде утечки через погонную проводимость G переходит на другой провод  или корпус, а другая увеличивает заряд линии и замыкается между линиями через погонную ёмкость С в виде тока смещения.

Для практики важны решения для гармонических функций времени t, поэтому:

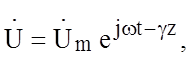                                       (1.3)

где  - амплитудное значение напряжения; w - круговая частота.

Подставляя (1.3) в (1.1) и (1.2), для синусоидального переменного тока можно получить:

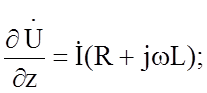                                          (1.4)

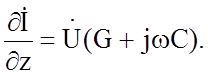                                          (1.5)

Подставляя (1.3) в (1.4), получаем

,                                     (1.6)

.

Назовем g постоянной распространения; a - коэффициентом затухания; b - фазовой постоянной.

Тогда из (1.6) характеристическое сопротивление определяем как

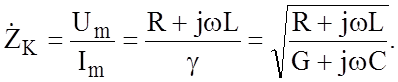                              (1.7)

Для малых затуханий в линии справедливо соотношение:

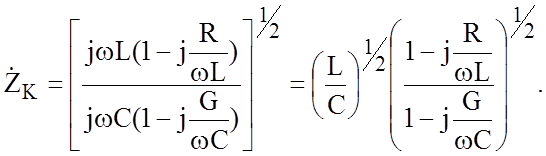                         (1.8)

С учётом приближенных выражений:

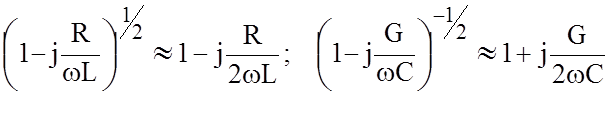
 определяем

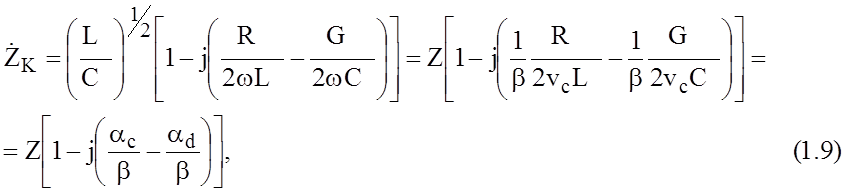
где  - скорость света, ,  - погонные потери в проводящих и диэлектрических средах.

Тогда по аналогии с выражениями для связанных коаксиальных и полосковых структур вводятся соотношения для характеристических сопротивлений нечетного «о» и чётного «е» типов возбуждения [7]:

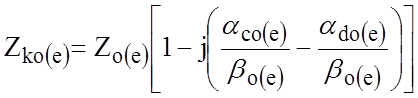.                                (1.10)

Таким образом, выражения (1.9), (1.10) позволяют более точно описывать длинные линии за счёт учёта погонных потерь, особенно это важно в миллиметровом и верхней части сантиметрового диапазонов.

С другой стороны, волновые сопротивления и эффективные диэлектрические проницаемости ЛП без учета потерь определяются через погонные емкости:

                 

                        ,

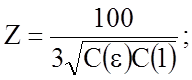
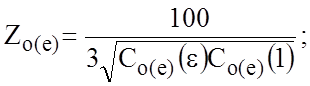
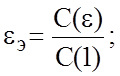
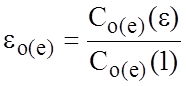где e - относительная диэлектрическая проницаемость; С(1), , , , пФ/см, - погонные емкости полосковых одиночных и связанных структур без диэлектрического и с диэлектрическим заполнением при неизменных конструктивных параметрах.

Учёт влияния дисперсии осуществляется по следующим соотношениям [8]. Для одиночной микрополосковой линии (МПЛ):

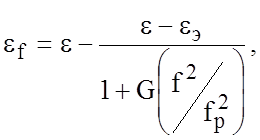
где 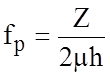; G @ 0,6+0,009Z - эмпирическая функция; h - толщина подложки, f - частота; m - магнитная проницаемость среды (для немагнитных материалов m=4p10^-7 Гн/м).

Для связанных МПЛ (СМПЛ):

,

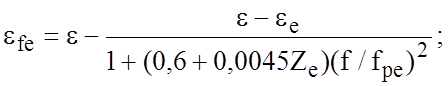
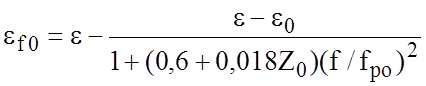где ,  - частотно-зависимые эффективные диэлектрические проницаемости при чётном и нечётном типах возбуждения;

 

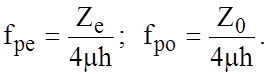
С целью учёта качества технологии изготовления полоскового проводника при определении a_с вводится понятие коэффициента потерь К_р [9], который даёт количественную оценку степени влияния микронеровностей поверхности на величину затухания:

,

где = 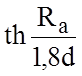- частотная поправка, зависящая от рабочей длины волны в ПЛ;  - среднеарифметическое отклонение микропрофиля; d - условная глубина проникновения волны;  - коэффициент шероховатости (отношение длины микропрофиля к длине идеально гладкой поверхности).

Значение поверхностного сопротивления  токонесущих поверхностей возрастает в К_p раз.

Вещественная часть поверхностного сопротивления, входящего в соотношения (1.9), (1.10), для двухслойной токонесущей поверхности, которая образуется при изготовлении ПЛ методами вакуумного осаждения, определяется соотношением: