Моделирование полосковых линий: Учебное пособие, страница 3

Таблица 1

Описание точки	Рисунок	Выражение для потенциала
	2	3
Обычная внутренняя точка
Точка на линии симметрии
Точка на пересечении двух линий симметрии
Точка на поверхности диэлектрика

Окончание табл.1

	2	3
Точка на остром угле диэлектрика			2	3
Точка на тупом угле диэлектрика
Точка на угле диэлектрика и линии симметрии

Для повышения точности результатов вычислений могут быть уменьшены расстояния между узлами путем их последовательного деления. Положение новых узлов точек должно определяться положением старых, а их потенциалы могут быть определены путем усреднения потенциалов четырех соседних, старых точек.

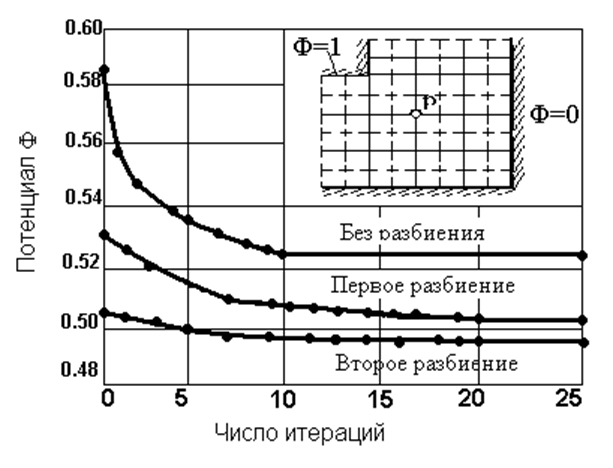
           Рис.1.2.  Изменение потенциала точки Р при последовательных

                          итерациях и разбиениях

     На рис. 1.2 показана зависимость потенциала фиксированной точки Р от числа итераций при последовательном уменьшении размеров ячеек сетки. Асимптотическое значение потенциала Ф различно для каждого разбиения, что обусловлено зависимостью ошибки вычисления от размеров ячеек. Из трех решений, полученных в результате последовательного деления ячеек, может быть экстраполировано четвертое, более точное. Если S₁, S₂ и S₃ – решения и n₁, n₂ и n₃ – число ячеек, приходящихся на единицу длины поперечного сечения (n₁< n₂< n₃), то более точное решение будет

S = b₁S₁ – b₂S₂ + b₃S₃,                                        (1.19)

где

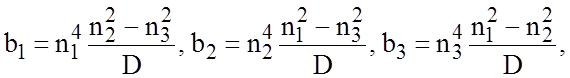
Необходимым условием существования экстраполированного решения является монотонная сходимость решений S₁,  и , которая в свою очередь зависит от того, сколь близок к единице коэффициент R, определяемый выражением

В этом выражении

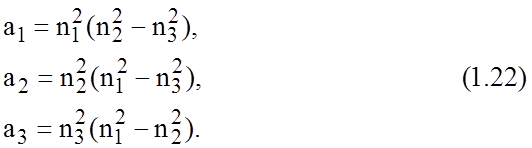
     Итак, получены все необходимые начальные предпосылки для расчета характеристик передающей линии, в которой может распространяться Т-волна. Для расчета самих характеристик линии необходимо проделать следующие операции. Сначала необходимо найти распределение потенциала в поперечном сечении линии. Это можно осуществить путем последовательного просмотра узловых точек, используя для этого приведенные выше итерационные формулы. Следующим шагом является расчет электрического заряда на единицу длины передающей линии. Для этого необходимо проинтегрировать нормальную составляющую электрического смещения вдоль поверхности, охватывающей один из проводников. Диэлектрическое смещение связано с электрическим потенциалом соотношением

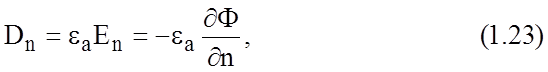
где  - нормальная составляющая смещения;  -  нормальная составляющая электрической напряженности и n – нормаль; ; =, Ф/м. Вновь воспользуемся методом конечных разно стей. С точностью а² нормальная составляющая производной потенциала точки Р может быть получена в виде

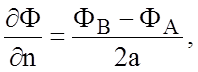
где  и  - потенциалы соседних точек А и В, лежащих по обе стороны от Р (рис.1.3). В этом случае интеграл, необходимый для определения полного заряда, может быть представлен в виде конечной суммы

где r — число узловых точек на отрезке, к которому принадлежит путь интегрирования; — число отрезков на пути интегрирования. Знак означает, что первый и последний члены в сумме для каждого отрезка должны быть уменьшены вдвое. Это соответствует формуле трапеции в численном интегрировании.

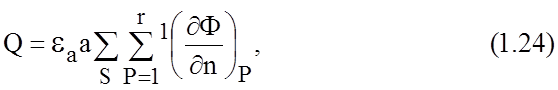
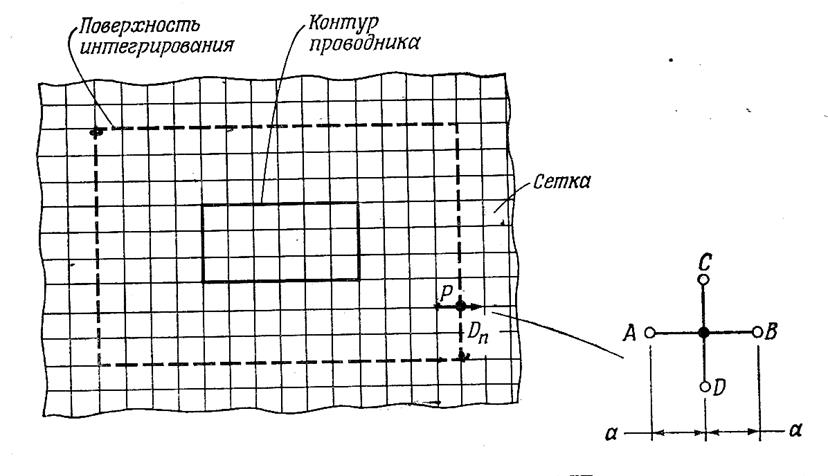Рис.1.3. Путь интегрирования

     Зная электрический заряд на единицу длины, можно найти электрическую емкость на единицу длины линии следующим образом:

                                                    С = Q ¤ U ,                                 (1.25)

где U= |Ф₂ – Ф₁| - разность потенциалов между проводящими поверхностями.

Если пространство в линии однородно, то характеристический импеданс равен

где L - индуктивность передающей линии на единицу длины. Из хорошо известного соотношения для Т-волн можно найти фазовую скорость в линии:

Следовательно, характеристический импеданс может быть найден как

В случае неоднородной среды индуктивность остается той же самой (в предположении, что диэлектрик немагнитен), однако емкость и, следовательно, фазовая скорость изменяется. В этом случае можно ввести понятие эффективной фазовой скорости, которая определяется как

где

 - эффективная диэлектрическая проницаемость среды.

Она определяется как отношение емкости линии при неоднородном заполнении (С) к емкости той же линии в случае, когда в качестве диэлектрика используется воздух ().

Объединяя выражения (1.28)-(1.30), для характеристического импеданса линии с неоднородной средой получаем

и

Существует несколько методов оценки точности найденных результатов. Одни из них заключается в нахождении задачи, которая имела бы известное аналитическое решение и при этом была бы максимально близка к рассматриваемой. Решив обе задачи при сравнимых начальных условиях численными методами и определив точность решения задачи, имеющей аналитическое решение, можно оценить точность решения и нашей задачи. Другой метод основан на том, что точность решения уравнения Лапласа определяется тем, насколько близки друг другу интегралы от градиентов поля, взятые по внутренней и внешней границам. Располагая такими данными, можно решить уравнение Лапласа для любых передающих линий с волной типа - Т, что позволяет определить для них характеристические импедансы и фазовые скорости.

В качестве первого примера рассмотрим линию, показанную на рис. 1.1. Поперечное сечение анализируемой линии имеет ось симметрии. Поэтому расчет можно вести только для одной половины сечения. Обратившись к рис. 1.4, мы видим, на сколько элементарных ячеек разбит каждый размер поперечного сечения.

Программа состоит из трех частей — основная программа и две подпрограммы. Основная программа задает граничные и начальные условия, вызывает подпрограммы, вычисляет конечный результат и коэффициент экстраполяции результата при последовательном делении элементарных ячеек. Первая подпрограмма, названная САР, определенное число раз, которое устанавливается основной програм­мой, просчитывает потенциалы последовательно всех точек и вычисляет емкость на единицу длины. Вторая подпрограмма, названная RЕС, предназначена для вычислений при переходе к меньшим размерам элементарных ячеек. Она заносит в оперативную память машины новые координаты всех старых узловых точек, а для каждой новой точки вычисляет и запоминает среднее значение потенциала четырех близлежащих точек.