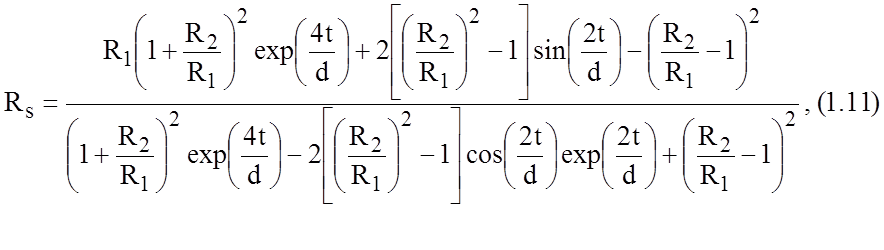Моделирование полосковых линий: Учебное пособие, страница 2

где  - удельное сопротивление адгезионного подслоя;  - удельное сопротивление материала проводника; t - толщина адгезионного подслоя; d - глубина скинслоя для адгезионной плёнки.

Таким образом, рассмотренные выше функции погонных потерь, входящие в матричные выражения для базовых элементов с учётом (1.11), позволят оценить влияние технологического процесса на выходные характеристики.

1.2. Методы анализа полосковых линий

Решение уравнения Лапласа разделением переменных. Уравнение Лапласа для скалярного потенциала Ф можно представить в виде:

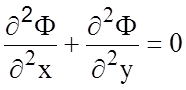×                                            (1.12)

Предположим, что переменные разделяются:

Ф=F₁(x)F₂(y).                                                (1.13)

После подстановки соотношения (1.13) в (1.12) получаем:

.

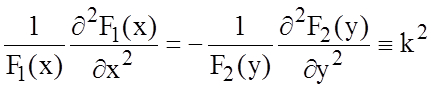Отсюда

где k - произвольная постоянная.

Задача в дальнейшем сводится к нахождению функции 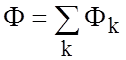, удовлетворяющей соответствующим граничным условиям при идеальности проводников.

Решение уравнений Лапласа методом комплексных переменных, конформное преобразование. Введем аналитическую функцию c(z), где z=x+jy и c=Ф+jy. Вещественная часть c именуется скалярным потенциалом Ф; мнимая часть является функцией потока y. Обе функции Ф и y удовлетворяют дифференциальным уравнениям Коши - Римана:

,                ,

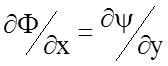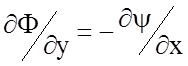а также уравнению Лапласа

,            ×

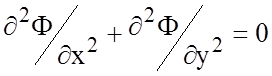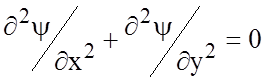Уравнения Коши - Римана определяют конформные преобразования между плоскостями c и z, на которых два семейства кривых, одно - для Ф=сonst и другое - для y=const, ортогональны.

Для решения внутренней электродинамической задачи необходимо найти функцию, удовлетворяющую граничным условиям, которые и определяют конструктивные особенности ЛП. Конформные преобразования позволяют изменить заданную геометрическую конфигурацию ЛП в такую, для которой решение задачи известно. Напряженности электрического и магнитного полей выражаются при этом в виде:

,     ;     ,

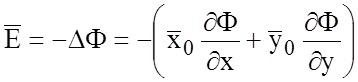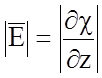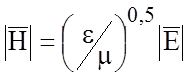где - единичные орты.

Решение уравнения Лапласа методом сеток [15]. Предполагается, что в линии распространяется только Т-волна. Область между проводниками делится на квадраты сеткой пересекающихся горизонтальных и вертикальных линий, и бесконечное число точек этой области заменяется конечным числом узловых точек, лежащих на пересечении этих линий. Допустим, нам необходимо рассчитать передающую линию, поперечное сечение которой представлено на рис. 1.1.

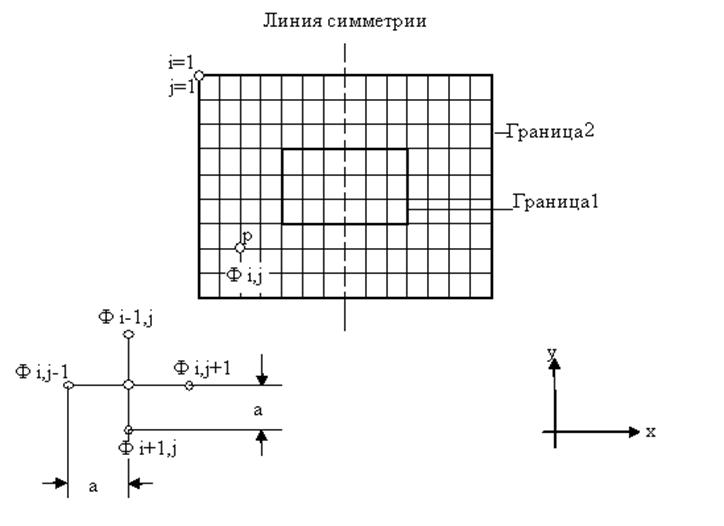
Рис. 1.1.  Схема сетки для расчета полей методом конечных разностей

В этом примере границы параллельны сетке линий. Это удобно при использовании ЭВМ. Ограничимся тем, что будем рассматривать только декартовы координаты. Тогда дифференциальное уравнение для потенциальной функции Ф(x,y) является уравнением Лапласа (1.12). Поскольку границы являются проводниками, то

Ф(x,y) = Ф₁     на границе 1,

Ф(x,y) = Ф₂     на границе 2.

Если поперечное сечение имеет ось симметрии, то, используя дополнительное граничное условие ¶Ф/¶n = 0 на этой оси, решение можно искать лишь для части области. На рис.1.1 строки и столбцы узлов обозначены i и j соответственно. При решении методом конечных разностей функция Ф(х,y) заменяется функцией , которая определена только для дискретного числа узловых точек. Эта функция должна удовлетворять уравнению (1.12). Для того, чтобы воспользоваться выражением (1.12) для числовых расчетов, выразим потенциал  точки Р через потенциалы четырех соседних с ней точек, ограничимся вначале однородной средой и предположим, что ширина элементарной ячейки равна  a. Тогда, применяя теорему Тейлора для направления вдоль оси х, получим:

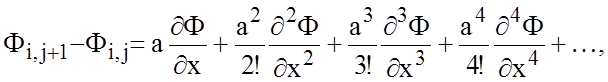
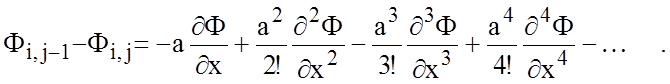
В результате суммирования этих выражений найдем

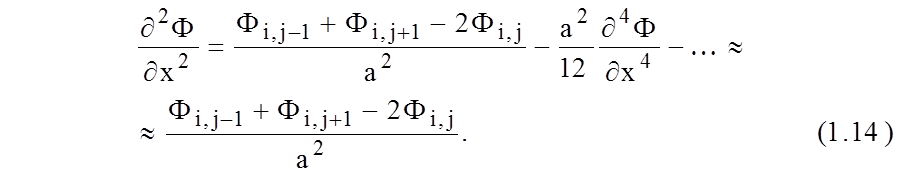
Это приближение имеет точность порядка а². При уменьшении расстояния между узлами точность результата может быть увеличена. Применив теорему Тейлора для направления вдоль оси y и, использовав

полученный выше результат, представим уравнение (1.12) в виде

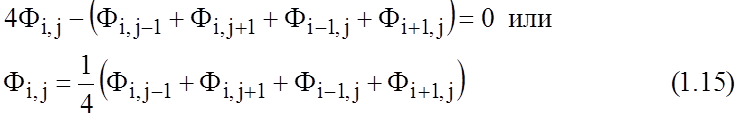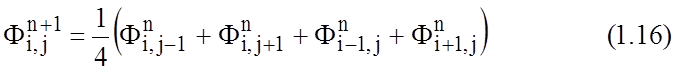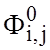Это выражение связывает потенциал каждой точки с потенциалами соседних с ней точек. Потенциалы точек, лежащих на проводящих границах, определяются граничными условиями. Для решения конкретной задачи уравнение (1.15) может использоваться как итерационная формула. Начальные значения потенциала внутренних точек  выбирается произвольно. Соотношение для последующих значений 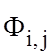 получается из (1.15) в виде выражения Рича

где 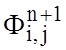 - потенциал точки Ф после (n+1) итерации. Уравнение (1.16) связывает этот потенциал с величинами потенциалов близлежащих точек, полученных после n-й итерации. Целью является получение ряда значений 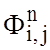, сходящихся к величине  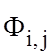после многократного просмотра всех узловых точек пространства вдоль строк и столбцов. Однако использование выражения (1.16) для численных расчетов неудобно тем, что в оперативной памяти машины необходимо хранить два последовательных значения потенциала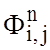 и 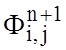 для всех точек сетки. Более удобным является выражение, при котором во время последовательного просмотра точек сетки сразу необходимо заменять в памяти машины старые значения потенциалов на новые. Этот способ приводит к более эффективной итерационной формуле

Для лучшей сходимости итерации нужно использовать так называемый ускоряющий коэффициент. С этим новым параметром итерационная формула примет следующий вид:

При k=1 выражение (1.18) совпадает с (1.17). В дальнейшем будем рассматривать только простейший случай, когда k=1.

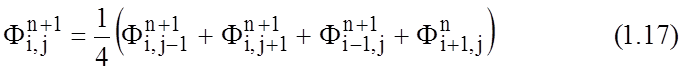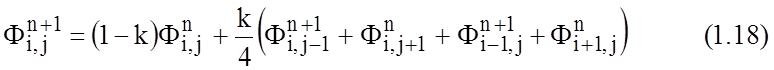Выше предполагалось, что область между проводниками однородна.             

Если передающая линия частично заполнена диэлектриком, то в такой линии волна типа Т в чистом виде распространяться не может, и поэтому характеристический импеданс не может быть рассчитан обычным образом. Однако, пока поперечные размеры линии много меньше половины длины волны, высшие типы волн не могут распространяться, и статическая аппроксимация дает хорошие результаты.

При решении уравнения Лапласа для линии с неоднородным заполнением полученное выше выражение (1.18) остается справедливым для всех точек сетки, кроме точек, расположенных на границе между двумя диэлектриками  с e ¹1 и e =1, а также точек, лежащих на линии симметрии, и угловых точек. Разностные уравнения для них могут быть получены из формул Тейлора, как и в однородном случае, однако здесь необходимо учесть дополнительные условия, сводящиеся к тому, что нормальная составляющая смещения должна быть непрерывной на границе раздела диэлектриков, а потенциал точки, лежащей с одной стороны от линии симметрии, должен быть равен потенциалу зеркальной точки. Уравнения для всех возможных случаевприведены в табл. 1.