Моделирование полосковых линий: Учебное пособие, страница 5

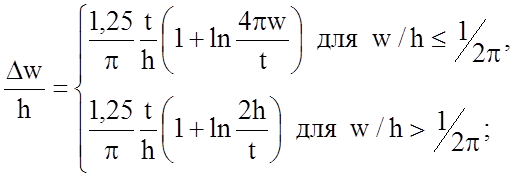
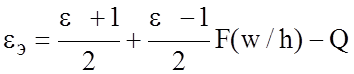,                          (2.8)

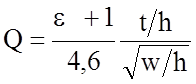           ,                 F(w/h) = (1+10h/w)^-1/2.                       

Максимальная относительная погрешность расчета величин Z и e_э по приведенным формулам не превышает 2 %.

Влияние дисперсии.Результаты исследования влияния частоты на волновое сопротивление и эффективную диэлектрическую проницаемость могут быть представлены в виде:

;

,

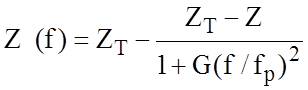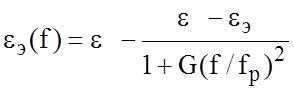где 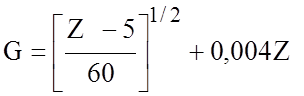 ;          f _p= 0,3976Z/h.

В этих уравнениях f_р измеряется в ГГц, h - в миллиметрах, Z - в омах, а Z_T - волновое сопротивление ПЛ шириной w и высотой 2h.

Потери. Формула потерь в проводниках a_с (дБ/м), полученная при использовании (2.6), может быть записана в виде

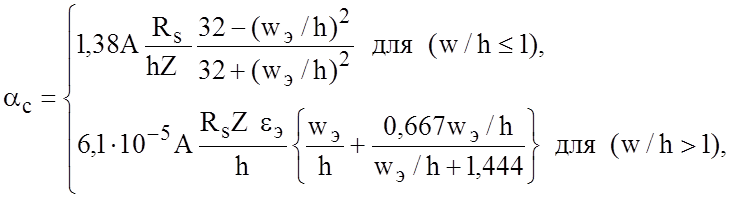
где w _э/h определяется из (2.7),

,

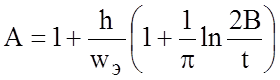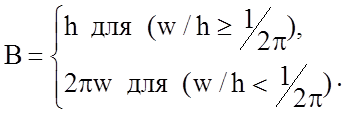
Потери в диэлектрике a_d (дБ/м) определяются формулой:

.                                 

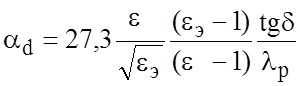     Потери в диэлектрике обычно существенно меньше потерь в проводниках вплоть до сантиметрового диапазона.

Функции чувствительности. Функции чувствительности показывают степень влияния соответствующих конструктивных параметров на Z или e_э. Для МПЛ функции чувствительности при t=0 имеют вид:

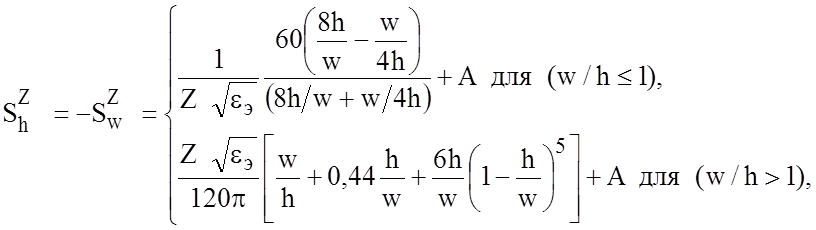
где                         ; ;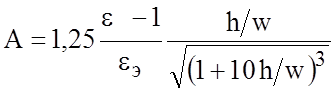

;     .

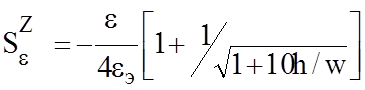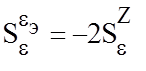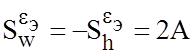2.3. Симметричная щелевая линия (СЩЛ)

Конфигурация СЩЛ приведена на рис. 2.3. Выражения в замкнутой форме для волнового сопротивления и длины волны в СЩЛ найдены путем аппроксимации соответствующих кривых, полученных численным расчетом.

Рис. 2.3. СЩЛ

Погрешность этих формул не превышает 2 % для следующих значений параметров: 9,7£ e £ 20,   0,02£w/h£ 1,   0,01£h/l_p£(h/l_p)_кр, где (h/l_p)_кр - есть отношение h/l_p, соответствующее критической частоте для поверхностной волны CЩЛ типа Н₁₀. Это отношение определяется формулой:

(h/l_p)_кр = 0,25/.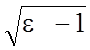

Формулы для расчета параметров линии различны при разных значениях отношения w/h.

Для 0,02£W/h£0,2	Z=72,62 - 15,283lne + 50(w/h - 0,02)(w/h - 0,1)/(w/h) + +ln(w/h.102)(19,23 - 3,693lne) - [0,139lne - 0,11+w/h´ ´(0,465lne +1,44)](11,4 - 2,636lne - h/lp.102)2; eэ=[0,923 - 0,195lne + 0,2w\h - (0,126w/h + +0,02)ln(h/lp×102)]-2×
Для 0,2<w/h£1	Z=113,19 - 23,257lne +1,25w/h(114,59 - 22,531lne)+ +20(w/h-0,2)(1-w/h) - [0,15+0,1lne + w/h(-0,79 + + 0,899lne)][10,25-2,171lne +w/h(2,1-0,617lne)-h/lp.102]2; eэ=[0,987 - 0,21lne + w\h(0,111 - 0,002e) - (0,053 + +0,041w/h - 0,0014e)ln(h/lp×102)]-2×

2.4. Копланарный волновод (КВ)

КВ находят широкое применение в интегральных СВЧ схемах. Использование КВ в СВЧ устройствах повышает гибкость конструирования, упрощает исполнение при реализации некоторых устройств как в планарном, так и в объемном вариантах.

Рис 2.4. КВ

Конфигурация КВ показана на рис.2.4. Анализ осуществляется квазистатическими и волновыми методами.

Волновое сопротивление и эффективная диэлектрическая проницаемость. Для диэлектрика конечной толщины запишем:

,

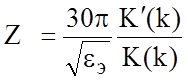где  k = s/(s+2w),

     

.

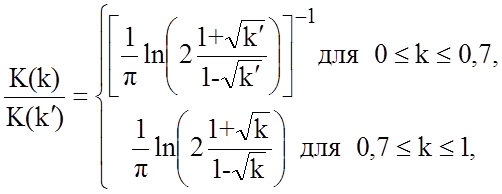
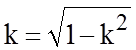Выражение для эффективной диэлектрической постоянной в замкнутой форме имеет вид:

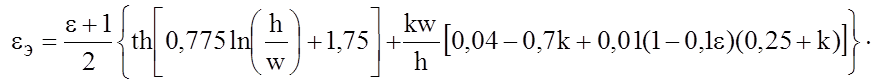
Точность этого выражения не хуже 1,5 % для e ³ 9,   h/w³ 1 и 0 £ k £ 0,7.

Влияние толщины полосковых проводников.Приведенные формулы получены в предположении бесконечно малых толщин полосковых проводников и заземленных пластин. Но практически металлизированный слой имеет конечную толщину t, которая влияет на характеристики. Влияние толщины полосковых проводников на волновое сопротивление КВ может учитываться введением эффективных значений ширины полосок s _э и зазоров w_э. Для КВ:

s_э = s+D ,

w_э = w-D ,

где D может быть найдено практически для любых значений s/h по формуле

D = (1,25p)[1+ln(4ps/t)] .

Волновое сопротивление может быть рассчитано по формуле:

,

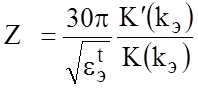где     k_э = s _э / (s _э+2w_э) @ k + (1 - k ²) D / 2w ,

а  - эффективная диэлектрическая постоянная для КВ с полосками толщиной t. Выражение для  может быть получено добавлением в формулу емкости КВ члена  Ae_be t/w, учитывающего возрастание емкости, которое возникает из-за влияния толщин металлических полосок. Величина А определяется эмпирически из условия совпадения расчетных значений  с численными значениями:

.

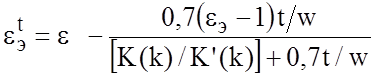Потери.При квазистатическом приближении для оценки активных потерь можно использовать формулу, учитывающую возрастание индуктивности. Тогда для затухания получим:

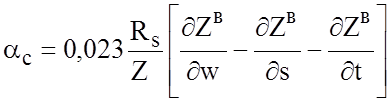.                               (2.9)

После подстановки в (2.9) выражений для частных производных получим окончательное выражение для потерь в проводниках (дБ/м):

,

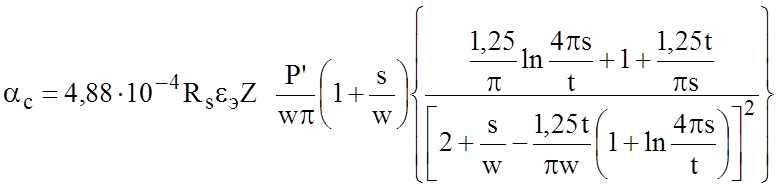где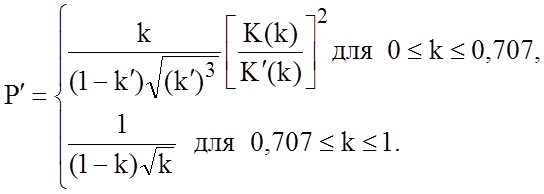                               

Потери в диэлектрике  (дБ/м) определяются, как и в МПЛ. В этом случае e_э определяется формулой (2.8).

2.5. Четырехслойная полосковая линия

Для многослойной одиночной полосковой линии целесообразно воспользоваться вариационным соотношением, определяющим погонную емкость в квази-Т приближении и не требующим проведения обратных преобразований Фурье:

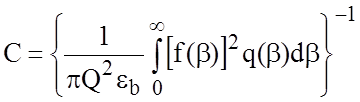,                            (2.10)

где 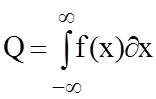 ; q(b) - функция, которая находится путем решения уравнения Пуассона для соответствующих граничных условий с помощью интегрального преобразования Фурье, для исключения дифференциальных операций по одной из координат.

Особенностью полученных выражений является то, что исходя из теоремыТомсона [14] заряды, находящиеся на системе заданных проводников, расположенных в диэлектрике, распределяются по поверхности этих проводников таким образом, что энергия, получающаяся в результате действия электрического поля, минимальна. Поэтому в соотношении (2.10) “пробная” функция f(x), вводимая из полуэмпирических соображений, уточняется исходя из вариационного принципа максимизации приведенных функционалов:

max ,  f(x)ÎR,                                       (2.11)

где ={C, } - вектор погонных емкостей.

Функция q(b) определяется формулой:

	Рис. 2.5. Четырехслойная ПЛ

Отсюда нетрудно перейти к частным случаям, исключая соответствующие слои. Например, для открытой МПЛ и трехслойной ПЛ запишем:

;                                    

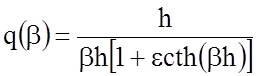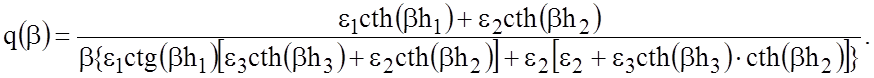
      Учет толщины ПЛ t можно осуществить, заменив функцию q(b) в выражении (2.10) на функцию вида:

,