Моделирование полосковых линий: Учебное пособие, страница 6

где                                    .

Как показывают теоретические и экспериментальные исследования, функция f(x) быстро возрастает при удалении от центра полоски, поэтому распределение плотности заряда можно представить в виде степенного ряда:

f(x)=a₀+a₁|x|+a₂|x|²+...,  xÎ(-w/2, w/2);  

f(x)=0,  xÎ[-¥, -w/2], xÎ[w/2,¥].                            (2.12)

Коэффициенты этого ряда выбирались из условия (2.11). Исследования данного вариационного соотношения показали, что точность определения величины погонной емкости слабо зависит от вида пробной функции f(x). E. Yamashita были предложены функции (2.13), (2.14), которые позволили сократить вычислительный процесс по сравнению с формулой (2.12) и обеспечить достаточную точность расчетов.

Таблица 2

Функция распределения плотности зарядов	Преобразование Фурье

Как показали теоретические исследования, функция (2.14) имеет характерную особенность при b®0. Эта особенность обусловлена тем, что при b=0 соотношение, стоящее в квадратных скобках, теоретически должно быть равно нулю, однако при расчетах на ЭВМ деление нуля на ноль невозможно, и поэтому полагаем, что b - малая, но конечная величина. Тогда полученное выражение в квадратных скобках, отличное от нуля, умножается на очень большое число. Указанную особенность можно устранить, введя ограничения вида b³10^-3, или считать, что при b<10^-3, f(b)=const.

2.6. Связанные симметричные полосковые линии

Конфигурация симметричной связанной  полосковой линии (ССПЛ) показана на рис.2.6. Для данного типа линий известны приближенные выражения в замкнутой форме для Ze и Zo, учитывающие конечную толщину полосковых проводников.

Рис. 2.6. ССПЛ

Формулы имеют наибольшую точность при t/b<0,1 и w/b³0,35:

,     ,

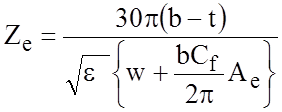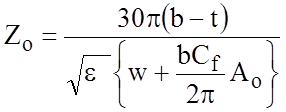где  1+ln(1+thQ)/ln2;

=1+ln(1+cthQ)/ln2;              Q=ps/(2b);

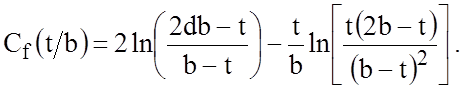
Суммарные потери в ССПЛ могут быть разделены на потери в диэлектрике  и потери в проводниках . Коэффициенты потерь (дБ/м) в диэлектрике и проводниках для четного и нечетного типов возбуждения определяются формулами:

= 

,

=

.

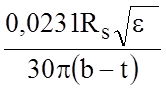
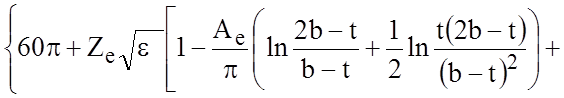
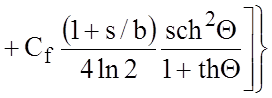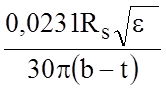
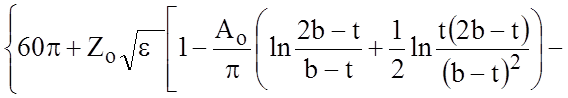
2.7. Связанные микрополосковые линии (СМПЛ)

Конфигурация СМПЛ показана на рис. 2.7. Свойства определяются значениями собственных и взаимных индуктивностей и емкостей. При квази-Т приближении собственная индуктивность может быть выражена через собственную емкость.

Рис. 2.7. СМПЛ

Cуммарные емкости при нечетном и четном возбуждении можно записать в виде:

C_e=C_p+C_f+C_f',       C_o=C_p+C_f+C_ga+C_gd,

где  C_p=ew/h, C_f, C_f', C_ga и C_gd - различные краевые емкости; C_f - краевая емкость МПЛ шириной w/h с волновым сопротивлением Z и эффективной диэлектрической постоянной e_э. Эта емкость может быть рассчитана по формуле:

Выражение для емкости C_f' получено эмпирически из условия совпадения значения емкости при четном возбуждении с численными результатами:

,

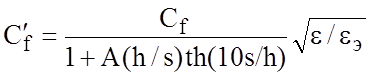где     A= exp(-0,1exp (2,33-2,53w/h)).

Емкость C_ga - составляющая, определяемая краевым полем в щели в свободном пространстве при нечетном возбуждении. Она может быть найдена из эквивалентной геометрии КВ:

C_ga=K(k')/K(k);      где k=(s/h)/(s/h+2w/h);      k'=,

а отношение полной эллиптической функции К(к) к дополнительной функции К(k¢) определяется так же, как и для КВ.

Емкость С_gd, определяемая краевым полем в щели внутри диэлектрика при нечетном возбуждении, может быть найдена путем изменения соответствующего выражения для емкости связанных ПЛ:

.

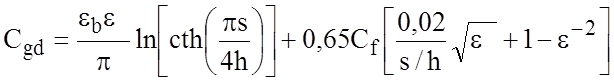Волновое сопротивление и эффективные диэлектрические постоянные при четном и нечетном видах возбуждения могут быть найдены из соответствующих значений емкости по следующим формулам:

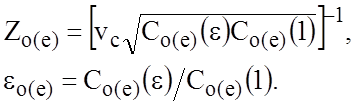
Если полосковые проводники имеют конечную толщину t, емкости могут быть рассчитаны с использованием понятия эффективной ширины для одиночной линии. Приведем выражения для эффективной ширины w_t, полученные путем соответствующего преобразования выражения для одиночной МПЛ. Эти выражения действительны для s³2t:

,

,

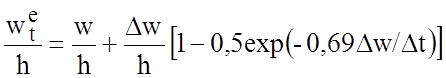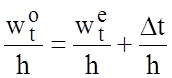где 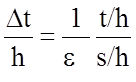    , Dw - приращение ширины полоски одиночной МПЛ, обусловленное влиянием толщины полоски t и определяемое формулой:

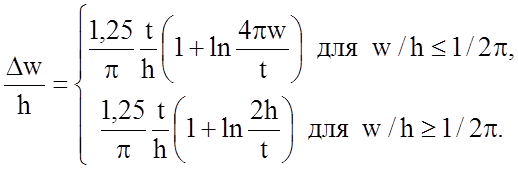
Дисперсионные свойства СМПЛ хорошо описываются численными методами. Широко распространены замкнутые выражения дисперсии эффективной диэлектрической постоянной, которые могут быть записаны в виде:

,

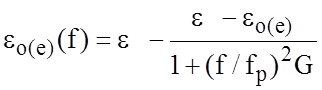где G=0,6+0,018 Z₀ - для нечетного возбуждения;

G=0,6+0,0045 Z_е - для четного возбуждения;

f_p=0,7952 Z₀/h - для нечетного возбуждения;

f_p=0,1988 Z_e/h - для четного возбуждения.

     Здесь f_p выражено в ГГц, а h - в миллиметрах. Дисперсионные свойства волнового сопротивления также могут быть описаны уравнением:

,

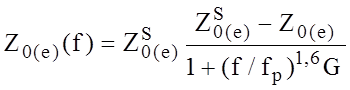где Z_0(e) - квазистатическое значение волнового сопротивления СМПЛ; 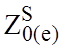- волновое сопротивление соответствующих связанных ПЛ с такими значениями s и w, как в СМПЛ, и расстоянием между заземленными пластинами, равным 2h. Значение 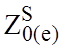 равно удвоенному значению, полученному по формулам:

,

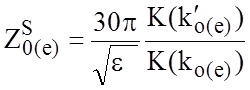где отношения K(k')/K(k) определяются так же, как для КВ;

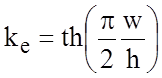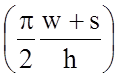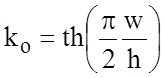 th;     cth;      .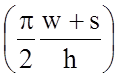

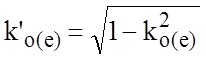Постоянные затухания, вызванные активными потерями, для четного и нечетного типов возбуждения для СМПЛ могут быть найдены по приращению индуктивности. Для конфигурации связанных линий получены следующие выражения постоянной затухания (дБ/м) при нечетном возбуждении:

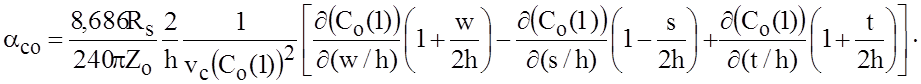
     Аналогично при четном возбуждении коэффициент затухания (дБ/м)

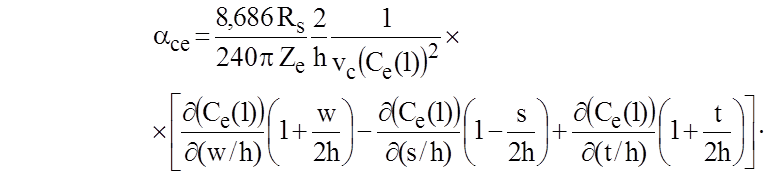
      Затухание (дБ/м), вызванное потерями в диэлектрике a_д, определяется как

,    ,

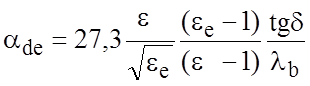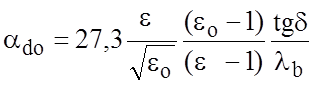где tgd - тангенс угла потерь диэлектрической подложки, а l_b  -  длина волны в свободном пространстве.

3. Интерфейс пакета прикладных программ

расчета полосковых линий ПОИСК-П

Общая структурная схема пакета показана на рис. 3.1. Пакет состоит из интерфейсной оболочки, с помощью которой производится ввод данных. В свою очередь, оболочка состоит из компонентов окна с установленными свойствами и подпрограмм основного модуля, осуществляющих формирование окна пакета.

ППП разработан под операционную систему Windows 95 на языке Delphi-3. При этом реализация алгоритмов осуществлена с использованием современных средств программирования и обработки данных.