Исследование методов обработки изображений с помощью пакета IMAGE PROCESSING TOOLBOX: Методические указания к лабораторным работам, страница 9

Главной причиной популярности методов, основанных на использовании масок пространственного дифференцирования, является простота их реализации на ЭВМ. Однако они чувствительны к шуму, присутствующему на изображении, и не могут гарантировать требуемый результат при обработке сложных естественных изображений.

Для преодоления этих недостатков были разработаны методы выделения контуров, сочетающие в себе процедуры подавления шумов и анализа производных яркости более высокого порядка. Метод Марра-Хильдрета, например, совмещает в себе обе процедуры путем вычисления свертки изображения с пространственным фильтром, представляющим собой дискретную аппроксимацию лапласиана от гауссоиды:

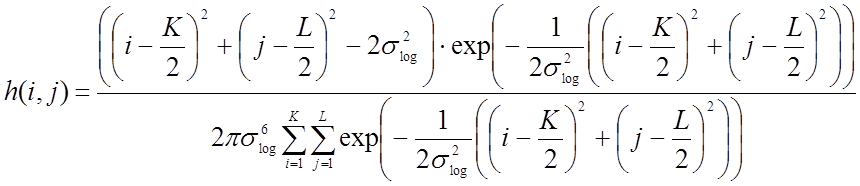 ,  (55)

где  – среднеквадратическое отклонение гауссоиды;  – размеры маски фильтра. Лапласиан (сумма вторых производных функции яркости по обеим координатам) обладает большей чувствительностью к перепадам яркости по сравнению с абсолютной величиной градиента, а использование гауссоиды для подавления шума позволяет повысить качество получаемого бинарного изображения, не внося существенных искажений в контурные линии исходного изображения.

Наиболее совершенным методом выделения границ в MATLAB Image Processing Toolbox является кэнни-метод (от англ. “canny” – хитрый, умный), в котором изображение предварительно сглаживается шумоподавляющим фильтром в виде гауссоиды, а градиентное изображение вычисляется путем свертки сглаженного изображения с фильтром, имеющим вид первой производной от той же гауссоиды, которая использовалась для подавления шумов. Пороговая обработка градиентного изображения осуществляется с использованием двух порогов для выделения “сильных” и “слабых” границ. Точки “слабых” границ включаются в бинарное изображение , только если они примыкают к точкам “сильных” границ. Таким образом обеспечивается бóльшая помехоустойчивость по сравнению со многими известными методами выделения границ.

Пример выделения контуров изображения различными методами приведен на рис. 3.

В MATLAB Image Processing Toolbox выделение контуров на изображении осуществляется функцией edge. В зависимости от выбранного метода вызов функции может иметь следующий вид:

1)  выделение контуров с помощью масок Собеля, Превитта или Робертса

J = edge(I, method, thresh),

где J – бинарное изображение ; I – исходное изображение ; method – метод выделения перепада яркости ('sobel', 'prewitt', 'roberts'); thresh – порог Т (постоянный для всех точек изображения). Если порог thresh не задан, то он выбирается автоматически в зависимости от статистических характеристик градиентного изображения ;

2) метод Марра-Хильдрета (с использованием лапласиана гауссоиды)

J = edge(I, 'log', thresh, sigma),

где sigma – среднеквадратическое отклонение  (по умолчанию );

3) кэнни-метод

J = edge(I, 'canny', thresh, sigma),

где sigma – среднеквадратическое отклонение шумоподавляющего фильтра (по умолчанию 1). Порог thresh может быть задан либо в виде вектора [lowhigh], либо скалярной величиной. В первом случае значение low используется для  выделения слабых границ, а значение high –  для выделения сильных. Во втором случае порог для выделения слабых границ вычисляется по правилу 0.4*thresh. Если порог не задан, то эти значения вычисляются автоматически на основе анализа статистических характеристик градиентного изображения .

а	б
в	г
д	е
Рис. 3. Выделение контуров изображения различными методами: а - исходное изображение; б - метод Собеля (порог Т = 0.1570); в - метод Превитта (порог Т = 0.1528); г - метод Робертса (порог Т = 0.2471); д - метод Марра-Хильдрета (порог Т = 0.0084); е - метод кэнни (“сильный” порог Тс = 0.1719 и “слабый” порог Тсл = 0.0688)

Качество контурного изображения, полученного с помощью различных методов выделения границ (Собеля, Превитта, Робертса, Марра-Хильдрета, кэнни), оценивается путем сравнения его с тестовым бинарным изображением , единичные точки которого соответствуют тем точкам исходного изображения, которые были выделены как минимум тремя методами из пяти. Результат сравнения контурных изображений , сформированных указанными методами, выражается в виде числа , вычисляемого по формуле

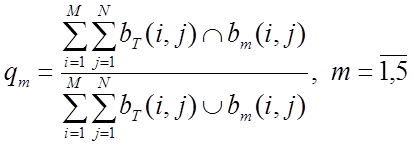.                            (66)

3. Порядок выполнения работы

1. Запустить систему MATLAB.

2. Знакомство с методами подавления шумов на изображениях.

2.1. Загрузить текст программы из файла, указанного преподавателем.

2.2. В открывшемся окне с текстом программы указать в качестве аргумента функции imread полное имя графического файла с исследуемым изображением, указанное преподавателем.

2.3. Исследовать способы подавления аддитивного гауссовского шума. Для этого в тексте программе задать переменной noise_typeзначение 'gaussian', переменной init_parameter– значение 0.0, переменной step_parameter – значение 0.002, переменной final_parameter – значение 0.01.

2.4. Запустить программу на выполнение. Визуально сравнить выведенные исходное, зашумленное и отфильтрованные изображения. Сделать выводы по поводу качества подавления аддитивных гауссовских шумов используемыми методами. Сохранить в отдельном файле график среднеквадратической ошибки сглаживания для разных масок.

2.5. Исследовать способы подавления импульсного шума. Для этого в тексте программе задать переменной noise_typeзначение 'salt & pepper', переменной init_parameter– значение 0.0, переменной step_parameter – значение 0.04, переменной final_parameter – значение 0.2.

2.6. Запустить программу на выполнение. Визуально сравнить выведенные исходное, зашумленное и отфильтрованные изображения. Сделать выводы по поводу качества подавления импульсного шума используемыми методами. Сохранить в отдельном файле график среднеквадратической ошибки сглаживания для разных масок.