5.5. Повторяя пп. 5.3, 5.4 для других значений порога связывания Т и координат стартовых точек, обеспечьте наиболее качественную сегментацию данного объекта с точки зрения критерия Q.
5.6. Поместите этот же тестовый объект в более темную однородную область кадра и повторите пп. 5.2 – 5.5.
5.7. Поместите этот же объект в область кадра с неоднородной яркостью и повторите пп. 5.2 – 5.5.
5.8. Повторите пп. 5.2 – 5.7 для другого тестового изображения объекта.
6. Изучение метода пространственного дифференцирования.
6.1. Заново загрузите исходный кадр и поместите в его самую светлую, однородную часть изображение первого тестового объекта. Выберите область обработки изображения, включающую тестовый объект.
6.2. В меню “Работа” выберите пункт “Простр. дифференцирование”. Найдите наилучшую маску, обеспечивающую наилучшую сегментацию с точки зрения критерия Q (результаты п.6 занесите в отчет).
6.3. Поместите этот же тестовый объект в более темную однородную область кадра и повторите п. 6.2.
6.4. Поместите этот же объект в область кадра с неоднородной яркостью и повторите п. 6.2.
6.5. Повторите пп. 6.2 – 6.4 для другого тестового изображения объекта.
7. Изучение Байесовского метода сегментации.
7.1. Заново загрузите исходный кадр и поместите в его самую светлую, однородную часть изображение первого тестового объекта.
7.2. В меню “Работа” выберите пункт “Байесовская сегментация”.
7.3. Выберите область обработки изображения (область окна), включающую тестовый объект и как можно меньше точек окружающего фона.
7.4. Изменяя разрядность гистограмм яркости и градиента, добейтесь наилучшей сегментации с точки зрения критерия Q (результаты п.7 занесите в отчет).
7.5. Увеличьте размеры окна вокруг объекта и повторите п. 7.4. Проанализируйте получаемые гистограммы и результаты сегментации.
7.6. Поместите этот же тестовый объект в более темную однородную область кадра и повторите пп. 7.2 – 7.5.
7.7. Поместите этот же объект в область кадра с неоднородной яркостью и повторите пп. 7.2 – 7.5.
7.8. Повторите пп. 7.2 – 7.6 для другого тестового изображения объекта.
8. Исследование влияния шума.
8.1. Загрузите исходное тестовое изображение.
8.2. В меню “Работа” выберите пункт “Добавить шум”, задайте параметры шума, после чего нажмите на кнопку “Запомнить шум”. Параметры шума задаются преподавателем.
8.3. Повторите пп. 4.3 – 4.5, 5.2 – 5.5, 6.2 – 6.4, 7.2 – 7.4 для одного тестового объекта.
9. Слежение за объектом.
9.1. Загрузите первый кадр из директории, указанной преподавателем, и задайте область интереса, содержащую объект. Из меню “Работа” выберите метод и его параметры, дающие наилучшие результаты (по предыдущим пунктам).
9.2. Запустите алгоритм слежения из меню “Работа” (п. “Слежение за объектом”). Для приостановки алгоритма слежения нажните на кнопку “Закрыть” в системном меню.
9.3. Качество работы алгоритма оцените визуально.
5. Библиографический список
1. Денисов Д. А., Низовкин В. Н. Сегментация изображений на ЭВМ // Зарубежная радиоэлектроника. 1985. № 11. С. 5-30.
2. Алпатов Б.А. Методы и алгоритмы обработки изображений в системах управления: Учеб. пособие. Рязань: РГРТА, 1999. 64 с.
3. Бакут П.А., Лабунец В.Г. Телевизионная следящая система с байесовским дискриминатором цели // Зарубежная радиоэлектроника. 1987. № 10. С. 81-93.
4. Путятин Е. П., Аверин С. И. Обработка изображений в робототехнике. М.: Машиностроение, 1990. 320 с.
5. Прэтт У. Цифровая обработка изображений: В 2-х т.: Пер. c англ. / Под ред. О. С. Лебедева. М.: Мир, 1982. 790 с.
6. Firooz Sadjadi. A Wavelet-Based Technique for Target Segmentation // Proc. of SPIE Vol. 2485 (Jul 1995). P. 54-59.
ЛАБОРАТОРНАЯ РАБОТА № 4
ИССЛЕДОВАНИЕ КОРРЕЛЯЦИОННЫХ АЛГОРИТМОВ ОПРЕДЕЛЕНИЯ КООРДИНАТ ОБЪЕКТОВ
В ПОСЛЕДОВАТЕЛЬНОСТИ ВИДЕОИЗОБРАЖЕНИЙ
1. Цель работы
Целью работы является исследование классических и разностных корреляционных методов определения координат объекта на изображении.
2. Теоретические сведения
Классический корреляционно–экстремальный алгоритм (КЭА) измерения координат объекта на изображении является частным случаем алгоритма поиска по критерию максимума апостериорной плотности в пространстве из двух параметров: координат центра объекта по горизонтальной и вертикальной осям [1,2]
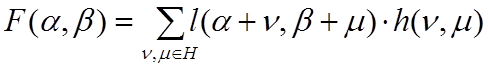, (21)
где 
-
элементы наблюдаемого изображения 
; 
- элементы дискретного эталонного
изображения объекта; 
и 
- координаты центра объекта в системе
координат изображения Ln (рис. 11); 
и 
-
координаты точек объекта в системе координат, связанной с центром объекта; n – номер кадра изображения.
Рис. 11 Координаты точек объекта в различных системах координат
Недостатками классического КЭА являются большое количество операций умножения, а также то, что он может давать грубые ошибки при наличии неоднородного фона на изображении. Если, например, яркость некоторых участков изображения окажется выше, чем яркость объекта, то взаимная корреляционная функция (21) даст неверный результат.
Для уменьшения влияния колебаний яркости изображения на точность определения координат используют нормированную взаимную корреляционную функцию
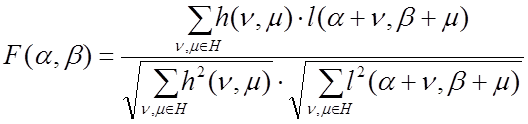. (22)
Но ее вычисление потребует значительного большего объема вычислительных операций [2]. Для снижения требуемого объема вычислений было предложено использовать вместо корреляционных критериальных функций так называемые разностные критериальные функции [1,2]. Алгоритмы определения координат центра объекта, построенные на их основе, также относят к группе КЭА.
Рассмотренный ранее классический корреляционный критерий можно отнести к критериям сходства двух изображений (эталонного и текущего). Существуют и другие критерии сходства (их можно найти в [1]), но их общим недостатком является необходимость перемножения элементов эталонного изображения (ЭИ) и текущего (ТИ), т. е. очень большой объем требуемых вычислений. В литературе все критерии сходства называют корреляционными функциями [1,2]. Разностные критериальные функции (следуя предложенной логике рассуждения) можно отнести к критериям отличия. Если критерии сходства требовалось максимизировать для нахождения координат центра объекта, то критерий отличия соответственно требуется минимизировать. По причине многоэкстремальности всех упомянутых критериев, порожденной неоднородным изображением фона, для отыскания глобального экстремума выбранного критерия целесообразно использовать метод полного перебора.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.