Исследование методов обработки изображений с помощью пакета IMAGE PROCESSING TOOLBOX: Методические указания к лабораторным работам, страница 8

где   – оценка идеального изображения ;  – наблюдаемое изображение ; PSF – импульсная характеристика искажающей системы , называемая также функцией рассеяния точки (point-spread function); NCORR – автокорреляционная функция аддитивного шума (обратное преобразование Фурье энергетического спектра ); ICORR – автокорреляционная функция идеального изображения.

Автокорреляционная функция идеального изображения может быть вычислена как

ICORR = fftshift(real(ifftn(abs(fftn(J.^2))),

где fftshift(…) – перегруппировка элементов матрицы спектральных коэффициентов, полученных в результате n-мерного преобразования Фурье таким образом, чтобы низкочастотные компоненты спектра занимали центральную часть матрицы; real(…) – вычисление действительной части комплексного числа; ifftn(…) – обратное n-мерное преобразование Фурье; abs(…) – вычисление абсолютной величины действительного или комплексного числа; fftn(…) – прямое n-мерное преобразование Фурье; .^2 – операция поэлементного возведения в квадрат всех элементов массива.

Автокорреляционная функция аддитивного шума вычисляется аналогично.

Параметры NCORR и ICORR являются необязательными. Если они не указаны, то функция deconvwnr реализует инверсный фильтр, определяемый выражением (11).

Импульсные характеристики фильтров, моделирующих основные типы пространственных искажений, задаются в системе MATLAB с помощью функции fspecial. В зависимости от используемой модели искажений вызов функции может иметь следующий вид:

1) размытие контуров изображения за счет смещения камеры в процессе формирования изображения

h = fspecial('motion', len, theta),

где h –  импульсная характеристика фильтра; len – величина смещения в пикселях; theta – направление смещения в градусах, отсчитываемое относительно горизонтальной оси против часовой стрелки;

2) снижение резкости изображения путем усреднения значений яркости каждой точки по окрестности, имеющей форму диска

h = fspecial('disk', radius),

где radius – радиус диска (по умолчанию – 5 пикселей); формируемая матрица h имеет размеры [2*radius+1 2*radius+1];

3) снижение резкости изображения путем свертки с дискретной аппроксимацией двумерной гауссоиды, вычисляемой по формуле

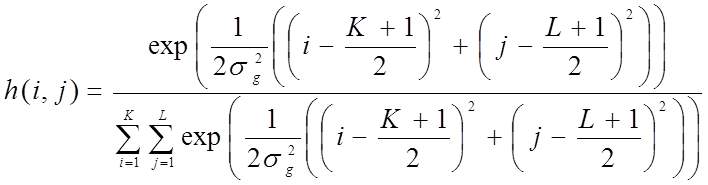
h = fspecial('gaussian', hsize, sigma),

где hsize – размеры формируемой матрицы h (по умолчанию – [3 3]); sigma – среднеквадратическое отклонение  (по умолчанию – 0.5).

Для случаев, когда априорная информация о свойствах пространственных искажений и статистических характеристиках изображения и шума недоступна, были разработаны методы слепой реставрации. В MATLAB Image Processing Toolbox для слепой реставрации изображений используется функция deconvblind, позволяющая получить итеративное уточнение оценки идеального изображения и грубой оценки функции рассеяния точки. Функция может быть вызвана следующим образом:

[J,PSF] = deconvblind(I,INITPSF),

где J – оценка идеального изображения ; PSF – оценка функции рассеяния точки; I – наблюдаемое изображение ; INITPSF – грубая оценка функции рассеяния точки.

Пример реставрации изображения описанными ранее методами с помощью функций, входящих в Image Processing Toolbox, приведен на рис. 2.

В качестве наблюдаемого изображения выбрано изображение биологических клеток живой ткани (см. рис. 1, а), искаженное фильтром типа ‘motion’ с параметрами len=31 и theta=11, к которому добавлен аддитивный гауссовский шум с дисперсией 0.002. При вычислении оценки идеального изображения методом слепой реставрации в качестве грубой оценки функции рассеяния использовалась матрица такого же размера, как и реальная функция рассеяния точки, состоящая из единиц. В MATLAB такую матрицу можно задать выражением

INITPSF = ones(size(PSF)).

2.3. Выделение контуров

Как правило, наиболее существенная информация о наблюдаемой сцене заключена в контурах изображения. Контуры содержат всю необходимую информацию о форме объектов, присутствующих на изображении, и операция выделения контуров очень часто облегчает последующий анализ наблюдаемой сцены (как визуальный, так и автоматический).

Самым популярным методом выделения контуров является метод пространственного дифференцирования [2], основанный на оценке скорости изменения (градиента) яркости для каждой точки наблюдаемого изображения. Если яркость меняется достаточно быстро, то точка находится на границе двух областей разной яркости, т. е. принадлежит контуру. Оценка абсолютной величины градиента яркости для дискретного изображения может быть вычислена по правилу

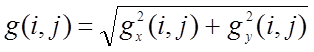 ,                                 (22)

где 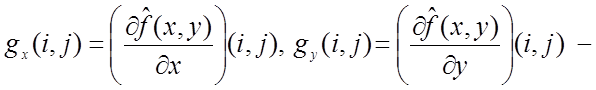 оценки частных производных, вычисляемые путем свертки массива исходных значений яркости  с маской оператора пространственного дифференцирования. Операторы пространственного дифференцирования являются по существу высокочастотными фильтрами. Чаще всего используются маски операторов Собеля, Превитта или Робертса, которые для случая выделения горизонтальных перепадов (вычисления ) имеют вид:

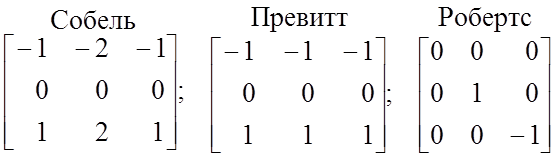.                     (33)

Маски операторов Собеля и Превитта для выделения вертикальных перепадов яркости (вычисления ) получаются из одноименных масок для выделения горизонтальных перепадов путем транспонирования, а маска оператора Робертса – поворотом на 90º по часовой стрелке.

Получаемый в результате массив  называют градиентным изображением. Далее осуществляется пороговая обработка градиентного изображения по правилу

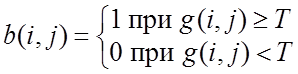   ,                               (44)

где Т – постоянный или меняющийся в зависимости от локальных свойств изображения порог. В результате получается бинарное изображение , единичные точки которого соответствуют потенциальным граничным точкам исходного изображения.