Исследование методов обработки изображений с помощью пакета IMAGE PROCESSING TOOLBOX: Методические указания к лабораторным работам, страница 7

H = [1 1 1; 1 1 1; 1 1 1]/9,

H = [1 1 1; 1 2 1; 1 1 1]/10, H = [1 2 1; 2 4 2; 1 2 1]/16.

Побочным эффектом всех описанных выше линейных фильтров является то, что в результате усреднения на профильтрованном изображении  часто пропадают мелкие детали, а контуры объектов становятся размытыми и нечеткими. Для преодоления этого недостатка были разработаны более совершенные методы подавления шумов, среди которых можно выделить винеровский и медианный фильтры.

Если наблюдаемое изображение повреждено аддитивным гауссовским шумом с нулевым средним и дисперсией , то метод подавления шума на основе адаптивного фильтра Винера обеспечивает меньшую размытость контуров и мелких деталей по сравнению с описанными ранее методами. В соответствии с этим методом яркости точек профильтрованного изображения  вычисляются на основе локальных оценок среднего значения  и дисперсии яркости  наблюдаемого изображения

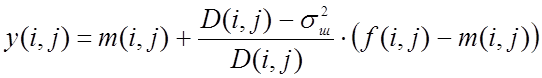 ,                     (6)

где 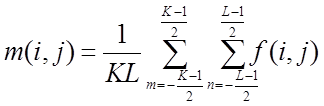; ; 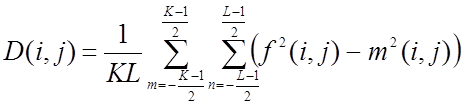K и L – размеры анализируемого участка изображения по вертикали и горизонтали соответственно.

В MATLAB Image Processing Toolbox подавление шума с помощью фильтра Винера осуществляется функцией wiener2, интерфейс которой имеет вид

J = wiener2(I,[m n],noise),

где J –  профильтрованное изображение; I –  наблюдаемое изображение;  [mn] –  размеры анализируемого участка изображения в пикселях по вертикали и горизонтали соответственно (по умолчанию – [3 3]);noise –  мощность аддитивного шума (произведение дисперсии  на количество точек изображения).

С помощью функций системы MATLAB мощность шума может быть вычислена как

noise = variance*prod(size(I)),

где variance – дисперсия шума ; prod(…) – функция, вычисляющая произведение элементов вектора; size(…) – функция, вычисляющая размерность многомерного массива (если массив имеет размерность k₁×k₂×…×k_n, то результат имеет вид вектора [k₁ k₂ … k_n]).

При вызове функции wiener2 параметр noise является необязательным. Если он не указан, то в качестве оценки дисперсии шума используется среднее значение всех локальных оценок .

Наиболее эффективным методом подавления импульсного шума (шума типа “соль и перец”) является медианная фильтрация. Это нелинейный метод обработки изображений, основанный на замене каждого элемента наблюдаемого изображения медианой всех элементов, попавших внутрь скользящего окна размером K×L, центр которого последовательно помещается в каждую точку изображения. (Медианой дискретной последовательности       а₁, а₂, …, а_N для нечетного N называется тот элемент последовательности, для которого существует (N–1)/2 элементов, не превышающих его по величине, и (N–1)/2 элементов, больше или равных ему по величине.) Медианный фильтр подавляет импульсные сигналы, длительность которых составляет менее половины ширины окна и вызывает уплощение вершины треугольных сигналов. Как правило, фильтр сохраняет контуры изображения, но иногда может искажать форму объектов. В частности, он скругляет острые (меньше 90º) углы ярких объектов на изображении.

Медианная фильтрация изображений в MATLAB Image Processing Toolbox реализована в виде функции medfilt2, которая может быть вызвана следующим образом:

J = medfilt2(I,[m n]),

где J – профильтрованное изображение; I –  наблюдаемое изображение;  [mn] –  размеры скользящего окна в пикселях (по умолчанию – [3 3]).

2.2. Реставрация изображений

Реставрацией называют процесс компенсации искажений наблюдаемого изображения  с целью получения оценки  некоего идеального изображения , которое наблюдалось бы на выходе идеального датчика, не вносящего никаких искажений. Искажения могут вноситься турбулентностью атмосферы, расфокусировкой оптики, недостаточным временем экспозиции, смещением датчика в процессе формирования изображения (размытость контуров наблюдаемых объектов) и т.п. Очевидно, что эффективность реставрации зависит от адекватности используемых моделей пространственных искажений. В литературе, посвященной цифровой обработке изображений, описание рассматриваемых ниже методов реставрации приводится для непрерывных изображений  и , хотя в действительности наблюдаемое изображение и получаемая оценка идеального изображения являются дискретными ( и  соответственно).

Пусть математическая модель искажений имеет вид двумерного линейного фильтра с импульсной характеристикой . Тогда частотная характеристика искажающего фильтра определяется как двумерное преобразование Фурье его импульсной характеристики

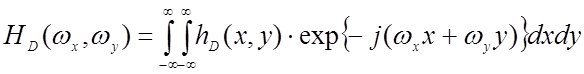  ,                (7)

где .

Если идеальное изображение рассматривается как реализация двумерного случайного процесса с нулевым средним и известным энергетическим спектром , а к искаженному изображению добавляется аддитивный гауссовский шум с нулевым средним и известным энергетическим спектром , то минимальная среднеквадратическая ошибка реставрации достигается использованием винеровского фильтра, частотная характеристика которого имеет вид

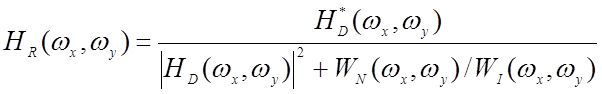  ,                        (8)

где ^* – знак комплексного сопряжения.

Оценка идеального изображения будет определяться как обратное двумерное преобразование Фурье произведения спектра наблюдаемого изображения и частотной характеристики реставрирующего фильтра, задаваемого выражением (8):

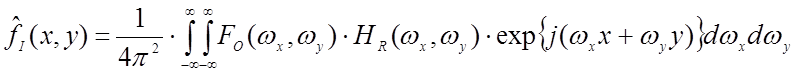 .   (9)

Если идеальное изображение не обладает пространственной корреляцией и его энергетический спектр принимает единичное значение во всем диапазоне пространственных частот  и , то выражение (8) приобретает более простой вид:

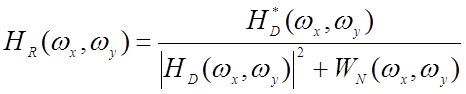   .                                  (10)

При отсутствии аддитивного шума винеровский фильтр вырождается в так называемый инверсный фильтр, имеющий частотную характеристику

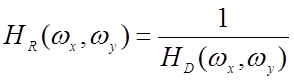  .                                               (11)

В MATLAB Image Processing Toolbox реставрация изображений с помощью винеровского фильтра реализована в виде функции deconvwnr, интерфейс которой имеет вид

 = deconvwnr(I, PSF, NCORR, ICORR),