Исследование методов обработки изображений с помощью пакета IMAGE PROCESSING TOOLBOX: Методические указания к лабораторным работам, страница 6

11. Построить гистограммы распределения уровней яркости  двух ранее полученных участков исходного изображения и вывести их в разных подокнах, расположив горизонтально.

12. Сделать на графике соответствующие поясняющие надписи: обозначения осей, заголовок.

6. Библиографический список

1. Мартынов Н.Н., Иванов А.П. Matlab 5.x. Вычисления, визуализация, программирование. М.: Кудиц-образ, 2000. 336 с.

2. Потемкин В.Г. Введение в Matlab. М.: Диалог-МИФИ, 2000. 256 с.

3. Рудаков П.И., Сафонов И.В. Обработка сигналов и изображений. Matlab 5.x / Под общ. ред. В.Г. Потемкина. М.: Диалог-МИФИ, 2000. 416 с.

ЛАБОРАТОРНАЯ РАБОТА № 2

МЕТОДЫ ФИЛЬТРАЦИИ ИЗОБРАЖЕНИЙ

1. Цель работы

Целью работы является знакомство с основными методами фильтрации применительно к различным задачам обработки изображений и способами их реализации в MATLAB Image Processing Toolbox.

2. Краткие теоретические сведения

Под фильтрацией изображения понимается его обработка линейными или нелинейными операторами (фильтрами) с целью придания обрабатываемому изображению желаемых характеристик. Цель обработки и свойства используемых фильтров различаются в зависимости от решаемых задач (реставрация изображений, подавление шумов, выделение границ и др.). Поэтому различные методы фильтрации далее будут рассмотрены применительно к конкретным задачам.

При реализации любых методов фильтрации изображений на ЭВМ исходное непрерывное изображение, описываемое функцией яркости , подвергается пространственной дискретизации с шагом  и квантованию по уровню. В результате получается матрица , элементами которой являются значения исходной непрерывной функции яркости в узлах дискретной решетки , округленные до ближайшего уровня квантования. Дальнейшей обработке подвергаются уже элементы матрицы F, которые будем обозначать . При обработке изображений в MATLAB Image Processing Toolbox с использованием описанных ниже функций элементы матрицы F предварительно преобразуются в формат double, в котором яркость полутонового изображения изменяется в диапазоне от 0 до 1 (0 – черный цвет, 1 – белый). Поэтому различные параметры вызываемых функций следует указывать с учетом того, что яркость точек изображения не превышает единицы.

2.1. Подавление шумов

Наблюдаемое изображение часто бывает искажено шумами и помехами различного физического происхождения: шумами видеодатчика, шумами зернистости фотоматериалов, ошибками в каналах передачи информации и др. При математическом описании искаженных изображений чаще всего используют аддитивный, импульсный и мультипликативный типы шумов.

Если идеальное (незашумленное) изображение обозначить , то наблюдаемое изображение , искаженное аддитивным шумом, можно представить в виде

,                                           (1)

где  - случайная функция, закон распределения которой чаще всего является гауссовским с нулевым средним и дисперсией .

Импульсный шум проявляется на изображении в виде отдельных точек с максимальной (белой) или минимальной (черной) яркостью. Белые точки часто называют “солевым шумом”, а черные – “перечным шумом”.

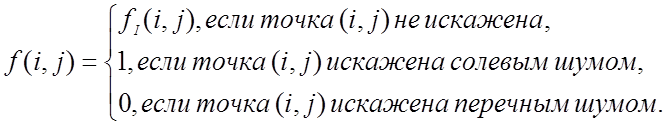              (2)

 Изображение , поврежденное мультипликативным шумом, можно представить в виде

,                                    (3)

где  - случайная функция, закон распределения которой в дальнейшем примем равномерным с нулевым средним и дисперсией . Пример изображения, поврежденного различными типами шумов, приведен на рис. 1.

В MATLAB Image Processing Toolbox зашумление изображения различными типами шума осуществляется функцией imnoise. В зависимости от вида шума функция может иметь разные форматы:

1) аддитивный гауссовский шум

J = imnoise(I,'gaussian',m,v),

где J–  зашумленное изображение; I –  исходное изображение; m –  среднее значение шума (по умолчанию 0); v – дисперсия шума (по умолчанию 0.01);

2) импульсный шум (“соль и перец”)

J = imnoise(I,'salt & pepper',d),

где d – плотность шума, т. е. отношение числа поврежденных точек изображения к общему числу точек (по умолчанию 0.05);

3) мультипликативный шум

J = imnoise(I,'speckle',v),

где v – дисперсия шума  (по умолчанию 0.04).

Как правило, шумы проявляются в виде разрозненных изменений отдельных элементов изображения и искаженные элементы могут заметно отличаться от соседних. На практике используются различные алгоритмы подавления шумов с помощью локальных операторов сглаживания (усреднения), являющихся по существу низкочастотными фильтрами. Элементы изображения , получаемого в результате обработки исходного изображения  двумерным линейным дискретным фильтром, импульсная характеристика которого задается матрицей H размерности K×L (K и L – нечетные), вычисляются по формуле дискретной свертки

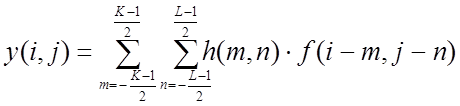,                              (4)

где  – элементы матрицы H. Подавление шумов обеспечивается низкочастотной фильтрацией с помощью матрицы  с положительными элементами. Наибольшее распространение получили следующие матрицы размерности 3×3, часто называемые шумоподавляющими масками:

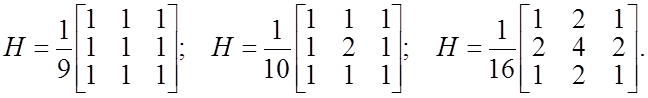                  (5)

Матрицы нормированы для получения единичного коэффициента передачи, чтобы процедура подавления шума не вызывала смещения средней яркости обработанного изображения. Существуют маски бóльших размеров (5×5, 7×7 и т.д.), но они используются реже.

В MATLAB Image Processing Toolbox фильтрация изображений шумоподавляющими масками может быть реализована с помощью функции imfilter, которая вызывается следующим образом:

J = imfilter(I,H),

где J –  профильтрованное изображение;  H– маска фильтра; I – исходное изображение. Маски фильтров, приведенных в выражениях (5), в системе MATLAB задаются следующим образом: