Математическое моделирование и оптимизация. Этапы построения математической модели. Методы оптимизации

Математическое моделирование и оптимизация

Объект – это часть среды, выделенная человеком с целью воздействия на него и получения желаемого результата. Объект связан со средой входными и выходными параметрами. Выходной параметр (Y) выдает информацию о состоянии объекта. Входные параметры (x₁, x₂, N) изменяют состояние объекта, т. е. вход – причина, выход – следствие.

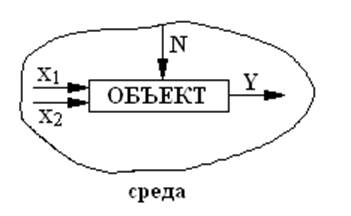
Рисунок 1

Входные параметры бывают:

1.   управляющие (например, x₁), которые можно измерить и изменить;

2.  возмущающие (например, x₂), которые можно только измерить, а изменить нельзя;

3.  помехи (N) – нельзя ни измерить, ни изменить.

МОДЕЛЬ – это упрощенное отображение оригинала. Модели бывают физические, описательные и математические.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ – устанавливает связь между входными и выходными параметрами в виде математического уравнения или системы уравнений.

Рассмотрим решение некоторых инженерных задач с использованием математических моделей.

1.  Задача управления решается в 4 этапа:

1.  Сбор информации о состоянии объекта и целях управления.

2.  Анализ полученной информации.

3.  Принятие решений на управление.

4.  Реализация принятого решения.

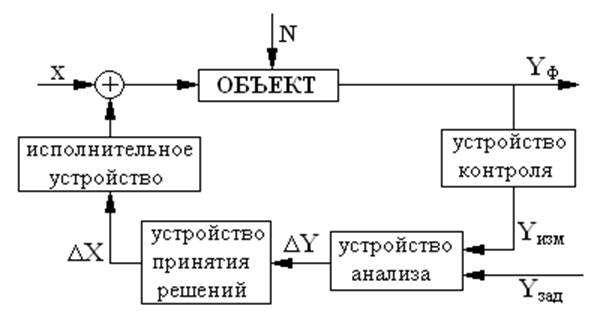
Рисунок 2

,

цель управления: .

 - Алгоритм уравнения

 - математическая модель

АЛГОРИТМ – обратная модель объекта, т.е. для эффективного управления объектами необходимо иметь математическую модель объекта.

2.  Задача обучения персонала

3 уровня обученности:

1)  Знания – обучаемый может воспроизвести ранее полученные теоретические знания.

2)  Умения – обучаемый умеет решать практические задачи на основе ранее полученных знаний.

3)  Навыки – обучаемый, не задумываясь, «автоматически» решает практически.

Уровень знаний и умений достигается в ходе лекционных лабораторных и практических занятий. Уровень навыков может достичь многократной тренировкой. Тренировку модно осуществить на реальном объекте или тренажере. Последнее предпочтительнее по экономическим соображениям.

Для отработки моторных навыков созданы различные виды тренажеров: от механических до компьютера.

Для отработки интеллектуальных навыков нужны тренажеры – имитаторы объекта, позволяющие имитировать расчетные задачи (интеллектуальные задачи). Это можно осуществить только с использованием математических моделей объекта и компьютерной техники.

  –  метод проб и ошибок

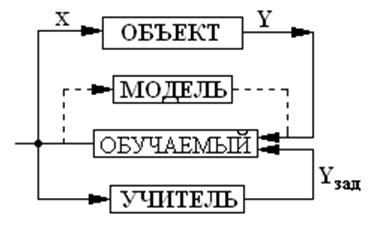
  – схема обучения на моделе – имитаторе

ТРЕНАЖЕР – это модель – имитатор, оснащенная системой представления информации, идентичной объекту.

Таким образом, в современных условиях обучение, повышение квалификации технологического персонала лучше всего проводить на тренажерах, в основе которых лежит математическая модель объекта.

3.  Задача организации и планирования производства

Например, организация планирования производства тортов.

Материалы	Расход на 1 кг		Ресурс на смену
	Прага	Медовый
мука, кг	0,3	0,5	50
маргарин, кг	0,1	0,2	30
сгущ.молоко, кг	0,2	0,1	30
сахар, кг	0,4	-	10
яйца, шт	4	3	200
сода, гр	10	10	1000
соль, гр	5	5	1000
коньяк, кг	0,1	0,15	25
масло, кг	0,2	0,1	30
шоколад, кг	0,1	0,1	10
мед, кг	-	0,4	30

1)

2) 0,3 + 0,5  50 – мука 

3) 0,1 + 0,2  30 – маргарин

    и т. д.

Максимальное количество тортов можно изготовить при условии, что неравенства () превратятся в равенства(=):

1		x=0	y=0
2	x×0,3 + y×0,5 = 50	y=100	x=160
3	x×0,1 + y×0,2 = 30	y=150	x=300
4	x×0,2 + y×0,1 = 30	y=300	x=150
5	x×0,4 = 10	-	x=25
6	x×4 + y×3 = 200	y=66	x=50
7	x×10 + y×10 = 1000	y=100	x=100
8	x×5 + y×5 = 1000	y=200	x=200
9	x×0,1 + y×0,15 = 25	y=166	x=250
10	x×0,2 + y×0,1 = 30	y=300	x=150
11	x×0,1 + y×0,1 = 10	y=100	x=100
12	y×0,4 = 30	y=75	-

4.  Диагностика неисправностей и прогнозирование отказов оборудования

5.  Задача исследования

Целью исследования является получение математической модели объекта, устанавливающей связь между входными и выходными параметрами, а затем получение новых знаний об объекте путем постановки опытов на модели.

Классификация математических моделей.

1.  По способу построения:

а)  детерминированные модели – модели, построенные на основе физико-химических законов;

б)  стохастические модели – строятся с использованием экспериментно-статистических методов.

Достоинства – недостатки:

Детерминированные модели универсальны, могут быть использованы на широком классе объектов, но сложны, дорогостоящи, требуют высокой квалификации исследователя.

Стохастические модели строятся дешево и быстро, квалификация исследователя не обязательно должна быть высокая; недостаток – может использоваться только на том объекте,  на котором проводился эксперимент.

2.  По свойствам объекта исследования:

а)  статические – выходные параметры не зависят от входных параметров, от времени;

б)  динамические – процесс развивается во времени (скорость, ускорение);

в)  стационарные – характеристики с течением времени не меняются;

г)  нестационарные – изменяются во времени;

д)  с сосредоточенными параметрами (параметры зависят от координат);

е)  с распределенными параметрами.

3.  По виду математических уравнений:

а)  алгебраические;

б)  тригонометрические;

в)  интегральные;

г)  дифференциальные и т.д.

4.  По применению:

а)  прогнозирующие модели – используются в задачах управления, где необходим прогноз при различных вариантах управления их параметрами;

б)  оптимизационные модели – используются для оптимизации процесса;

в)  модели-имитаторы объекта (тренажеры).

Этапы построения математической модели

1 этап – Сбор информации о целях построения модели, способах и точности ограничений по времени вычислений, полноте описаний и других характеристиках.

2 этап – Сбор информации об объекте

2 подэтапа:

1) сбор теоретических сведений об объекте,

2) сбор информации о вход - выходных параметрах объекта.

3 этап – Синтез структуры модели.

4 этап – Идентификация объекта (настройка коэффициентов модели).

5этап – Проверка адекватности модели.

6 этап – Использование модели по назначению и исследование объекта на этой моделе.

1 этап

Точность модели определяется из цели построения и измерения.

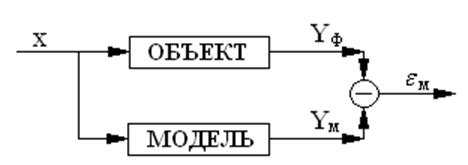
 – входные параметры,

 – выходные параметры  (фактические).

1)  – ошибка модели (абсолютная)

2) 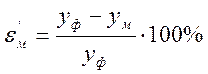 – относительная ошибка модели

3)  – модульная ошибка

4) для повышения чувствительности методов настройки модели к ошибке берут квадрат этой ошибки 

В зависимости от целей использования модели используют ту или иную ошибку э

Полнота описания Модель должна описывать объект структурно с заданной точностью.

Информационное подобие предполагает отображение входных и выходных параметров в том же виде, что и на реальном объекте.