Тогда, таблица наблюдений получается следующая:
|
№ серии |
№ опыта |
|
|
|
|
|
|
1 |
1 |
|||||
|
2 |
||||||
|
Ср |
||||||
|
2 |
1 |
|||||
|
2 |
||||||
|
Ср |
||||||
|
n |
3 Аналог спланированного эксперимента
объединяет положительные стороны активного и пассивного экспериментов.
Сначала составляется план активного эксперимента, затем из большого числа данных пассивного эксперимента выбираются опыты, соответствующие опытам в плане активного эксперимента, и результаты вносятся в матрицу планирования.
Обработка результатов эксперимента проводится как в активном эксперименте.
4 Получение таблицы наблюдений с помощью экспертных оценок
Эксперты подбираются из технологического персонала, обслуживающего исследуемый объект, имеющие большой стаж работы и хорошие производственные показатели.
3 этап Синтез структуры модели
Структура модели – это вид математической зависимости выходного параметра от входного.
Этот вид уравнения определяется свойствами объекта (например, линейный, гиперболический, параболический и т.д.).
Свойства объекта исследователь определяет при сборе теоретической информации. Это творческий субъективный процесс (синтез).
На примере активного спланированного эксперимента можно предложить следующую структуру модели:
![]()
![]() .
.
4 этап Идентификация объекта (настройка коэффициентов модели)
Осуществляется двумя способами:
1. Расчетный (аналитический)
2. Поисковый способ
Расчетный способ использует различный варианты метода наименьших квадратов.
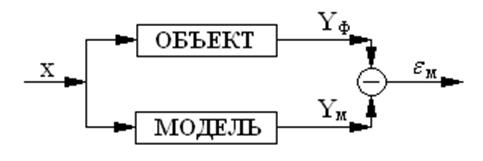
![]()
Метод наименьших квадратов (МНК)
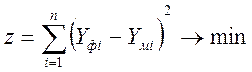
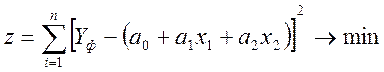 -
условие минимизации уравнения
-
условие минимизации уравнения
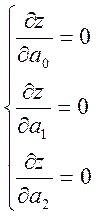
После дифференцирования получается система двух уравнений
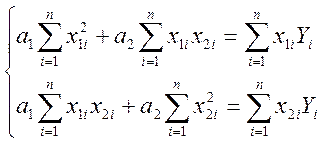
Однако, МНК позволяет получить точное несмещенные оценки коэффициентов только при выполнении некоторых предпосылок, важнейшими из которых является:
1.
Входные величины ![]() и т.д. должны измеряться с
точностью, как минимум на порядок превышающей точность измерения выходного
параметра.
и т.д. должны измеряться с
точностью, как минимум на порядок превышающей точность измерения выходного
параметра.
2.
Входные параметры ![]() и т.д. не должны быть коррелированны,
т.е. статистически связаны между собой.
и т.д. не должны быть коррелированны,
т.е. статистически связаны между собой.
3.
Выходной параметр ![]() должен быть случайной величиной,
подчиняющейся нормальному закону распределения
должен быть случайной величиной,
подчиняющейся нормальному закону распределения
4. Рассеяние (Дисперсия) выходного параметра не должна зависеть от его абсолютной величины.
1 и 2 – практически не выполняются на реальных объектах.
Выполнение вышеперечисленных предпосылок может обеспечить только при активном эксперименте, когда матрица планирования составляется с учетом выполнения этих предпосылок.
Применение МНК в пассивном эксперименте не дает гарантии получения точных коэффициентов модели.
Поисковый способ настройки коэффициентов модели («Метод подстраиваемой модели»)
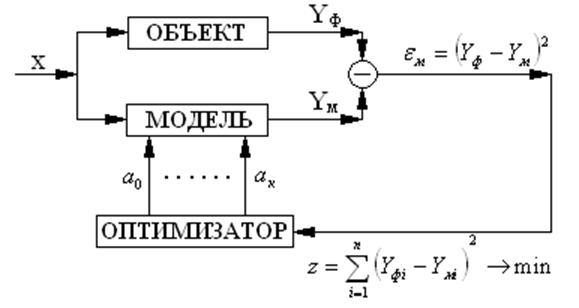
5 этап Статистическая обработка результатов и оценка адекватности модели
Наиболее распространенные статистические вычисления:
− среднее арифметическое значение;
− дисперсия;
− среднее квадратическое отклонение;
− корреляция;
− математическое ожидание;
− ошибка коэффициента корреляции.
Математическое ожидание случайной величины
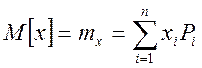 , где
, где ![]() - возможное значение случайной
величины,
- возможное значение случайной
величины,
![]() - вероятность этого значения.
- вероятность этого значения.
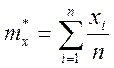 -математическое среднее.
-математическое среднее.
Дисперсия
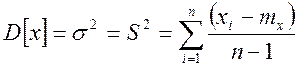
Средне квадратическое отклонение (СКО)
![]()
Коэффициент корреляции между двумя случайными величинами характеризует степень линейной связи между случайными величинами
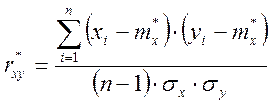
Статистическая обработка результатов эксперимента:
1. Проверка воспроизводимости опыта
G – критерий Кохрена
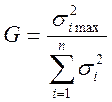
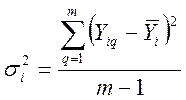 ,
,
где ![]() - максимальное
значение построчной дисперсии;
- максимальное
значение построчной дисперсии;
![]() - номер строки;
- номер строки;
![]() - номер
повторения опыта;
- номер
повторения опыта;
![]() - количество
повторений.
- количество
повторений.
Если ![]() , то опыты воспроизводимы.
, то опыты воспроизводимы.
Табличные значения критерия Кохрена выбираются из
статистических таблиц в зависимости от количества опытов (![]() ), числа степеней свободы
), числа степеней свободы ![]() и уровня значимости (надежности) P=0,95.
и уровня значимости (надежности) P=0,95.
2. Оценка значимости коэффициентов
Для этого определяется дисперсия эксперимента
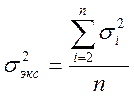
Усредненная дисперсия для повторных опытов
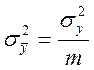
![]() -
среднеквадратическая ошибка коэффициента модели
-
среднеквадратическая ошибка коэффициента модели
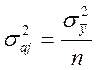
Доверительны интервал ![]() ,
,
где ![]() -
коэффициент Стьюдента (определяется по таблицам, выбирается в зависимости от
-
коэффициент Стьюдента (определяется по таблицам, выбирается в зависимости от ![]() , P=0,95).
, P=0,95).
Если
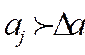 - следовательно коэффициент значим;
- следовательно коэффициент значим;
Если ![]() -
следовательно, коэффициент незначим,
-
следовательно, коэффициент незначим, ![]() обращается в 0.
обращается в 0.
3. Проверка адекватности модели
Критерий адекватности проверяют по критерию Кохрена.
Если ![]() - модель адекватна
- модель адекватна
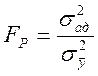
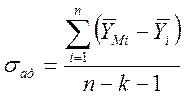 ,
,
где
![]() - модельное
- модельное ![]() ,
рассчитанное для
,
рассчитанное для ![]() строки,
строки,
![]() - количество факторов,
- количество факторов,
![]() -
среднее значение.
-
среднее значение.
![]()
![]()
![]() ,
,![]() - число степеней свободы
- число степеней свободы
![]() - табличное значение критерия Фишера
(определяется из таблиц по числу степеней свободы
- табличное значение критерия Фишера
(определяется из таблиц по числу степеней свободы ![]() ,
,![]() )
)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.