Если модель неадекватна, приходится возвращаться к третьему, а иногда и ко второму этапу моделирования, т.е. менять структуру модели или составляющих факторов, влияющих на выходной параметр.
Если модель адекватна, переходят к 6 этапу.
6 этап Использование модели по назначению и исследование объекта
С помощью модели можно спрогнозировать, что будет дальше.
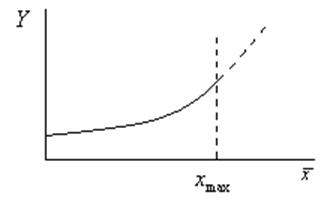
Методы оптимизации
Оптимизация – это процесс улучшения показателей работы объекта. К таким показателям относятся:
− производительность;
− себестоимость продукции;
− показатели качества.
Задача оптимизации относится к экстремальным задачам и может быть решена двумя способами:
1. с использованием расчетных (или аналитических) методов,
2. с использованием поисковых методов.
Оптимизация бывает одномерная и многомерная. В первом случае на показатель работы оптимизируемого объекта влияет один параметр, во втором – 2 и более.
Оптимизация может осуществляться непосредственно на объекте (прямая оптимизация) и на моделе этого объекта.
Оптимизация бывает условная и безусловная. В первом случае имеются ограничения на параметры оптимизации, во втором – их нет.
Рассмотрим методы оптимизации:
1. Беспоисковый (или аналитический) основан на исследовании производных.
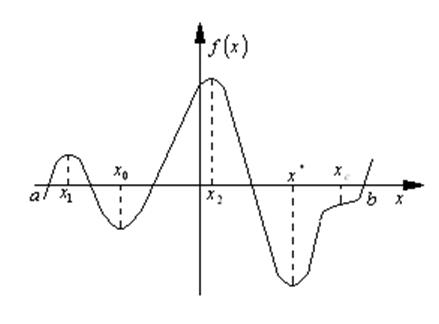
На отрезке ![]() необходимо
определить экстремум функции. Задачей является определение, например, минимума
функции на отрезке
необходимо
определить экстремум функции. Задачей является определение, например, минимума
функции на отрезке ![]() .
.
Решением задачи оптимизации является координата ![]() , значение функции
, значение функции ![]() при условии, что функция в этой
точке меньше всех других значений функции
при условии, что функция в этой
точке меньше всех других значений функции ![]() .
.
Производят следующие действия:
1.
Берется первая производная и
приравнивается к нулю ![]() , следовательно, мы найдем
, следовательно, мы найдем ![]() .
.
2.
Чтобы найти непосредственно
минимумы, берем вторую производную ![]() и определяем ее
знак:
и определяем ее
знак:
−
если ![]() ,
то
,
то ![]() ;
;
− если![]() ,
то
,
то ![]() .
.
Отсюда находим, что ![]() - минимумы.
- минимумы.
3.
Рассчитываем значения функции в
этих координатах ![]() ,
, ![]() и
сравниваем их
и
сравниваем их ![]() . Таким образом,
. Таким образом, ![]() и
и ![]() -
решения задачи оптимизации.
-
решения задачи оптимизации.
Параметр объекта, который улучшается, называется
критерием оптимизации. То есть функция ![]() -
это математическая модель объекта и в то же время эта зависимость выходного
параметра от входного является математическим выражением критериев
оптимизации.
-
это математическая модель объекта и в то же время эта зависимость выходного
параметра от входного является математическим выражением критериев
оптимизации.
2. Поисковый метод
Все поисковые методы решают задачу оптимизации в два этапа.
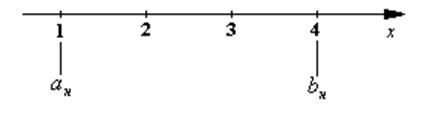
1 этап – определение границ исходного интервала
неопределенности. Интервалом неопределенности называют интервал между
координатами ![]() на оси
на оси ![]() ,
на котором находится искомый оптимум. Эта процедура поиска исходного интервала
неопределенности сводится к редкому исследованию функции (т.е. через большие
промежутки).
,
на котором находится искомый оптимум. Эта процедура поиска исходного интервала
неопределенности сводится к редкому исследованию функции (т.е. через большие
промежутки).
2 этап заключается в последующем уменьшении исходного
интервала неопределенности до заранее известной величины ![]() (точность метода) при условии, что
оптимум находится на уменьшаемом интервале неопределенности.
(точность метода) при условии, что
оптимум находится на уменьшаемом интервале неопределенности.
И решением задачи оптимизации в этом случае является
координата конечного интервала неопределенности ![]() и
значения функций в этих координатах.
и
значения функций в этих координатах.
Рассмотрим примеры методов поисковой оптимизации:
а) Метод сканирования
Имеется исходный интервал
![]() , точность метода -
, точность метода - ![]() .
.
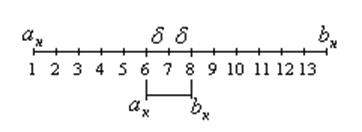
Через равные промежутки производится исследование интервала.
Суть метода – исследуется функция на отрезке ![]() через равные расстояния
через равные расстояния ![]() , т. е. производится расчет значений
функции в этих точках (координатах). Затем, значений функции сравниваются и
определяется минимальное значение.
, т. е. производится расчет значений
функции в этих точках (координатах). Затем, значений функции сравниваются и
определяется минимальное значение.
Если минимальное значение функции находится в точке 7,
следовательно, истинный минимум находится в интервале 6¸8 (![]() ,
,![]() ).
).
![]() -
условие, по которому определяется
-
условие, по которому определяется ![]() , тогда
, тогда 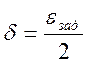 .
.
Метод сканирования требует большого количества опытов и практически не применяется.
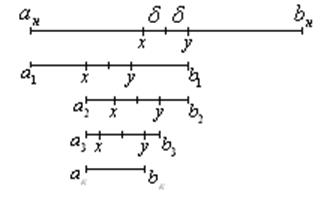
б) Метод половинного деления
На исходном интервале
неопределенности определяются 2 точки - ![]() и
и
![]() .
.
1) От середины интервала ![]() через равные отрезки
через равные отрезки ![]() откладываются точки
откладываются точки ![]() и
и ![]() .
.
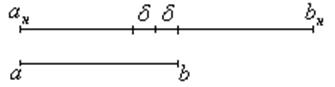
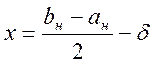
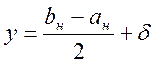
2) Рассчитываются значения функции в
точках ![]() и
и ![]() (
(![]() ,
, ![]() )
и сравниваются между собой.
)
и сравниваются между собой.
− если ![]() ,
то
,
то ![]() ,
, ![]() ;
;
− если ![]() ,
то
,
то ![]() ,
, ![]() .
.
3) Сравниваем интервал с точностью ![]()
− если ![]() ,
то идти к шагу 1;
,
то идти к шагу 1;
− если ![]() ,
то «КОНЕЦ».
,
то «КОНЕЦ».
![]()
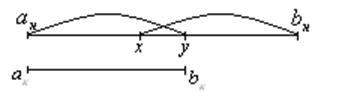
3. Метод золотого сечения
![]()
корни этого уравнения - ![]() ,
, ![]()
![]()
![]()
![]() ,
где
,
где ![]() - коэффициент сжатия.
- коэффициент сжатия.
Обычно используется ![]() - величина золотого сечения.
- величина золотого сечения.
![]()
![]()
Имеется интервал неопределенности.
1) Определяются ![]() ,
,
![]() .
.
2) Рассчитываются ![]() ,
, ![]() и
сравниваются между собой.
и
сравниваются между собой.
− если ![]() ,
то
,
то ![]() ,
,
![]() ,
,
![]() ;
;
− если ![]() ,
то
,
то ![]() ,
,
![]() ,
,
![]() .
.
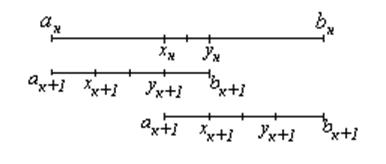
3) Проверка
− если ![]() ,
то идти к шагу 1;
,
то идти к шагу 1;
− если ![]() ,
4 шаг.
,
4 шаг.
4) Решением задачи оптимизации являются
координаты ![]() ,
, ![]() и
значения функций
и
значения функций ![]() ,
, ![]() .
.
4. Метод Фибоначчи
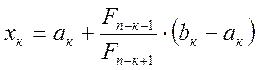 ,
,
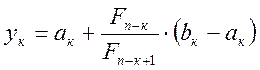 ,
,
где ![]() -
числа (ряд) Фибоначчи.
-
числа (ряд) Фибоначчи.
![]() ,
,
![]() .
. ![]()
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …
Методы многомерной
Оптимизации
Алгоритм расчета аналогичен предыдущим методам.
Многомерная оптимизация – имеется 2 и более факторов, влияющих на выходной параметр.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.