где адрес RC[1] является адресом ячейки, соответствующей приграничному узлу сеточной области и находящейся справа от ячейки, соответствующей узлу сеточной области на 1-ой границе.
В остальных граничных ячейках формулы реализуются аналогично, при этом приграничные ячейки имеют следующие адреса: на 2-ой границе R[1]C; на 3-ей RC[-1]; на 4-ой R[-1]C, а формулы имеют соответственно следующий вид
,
,
.
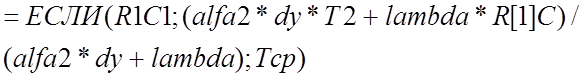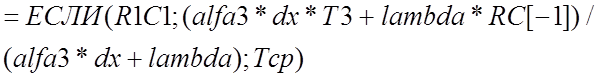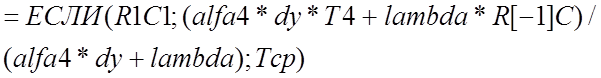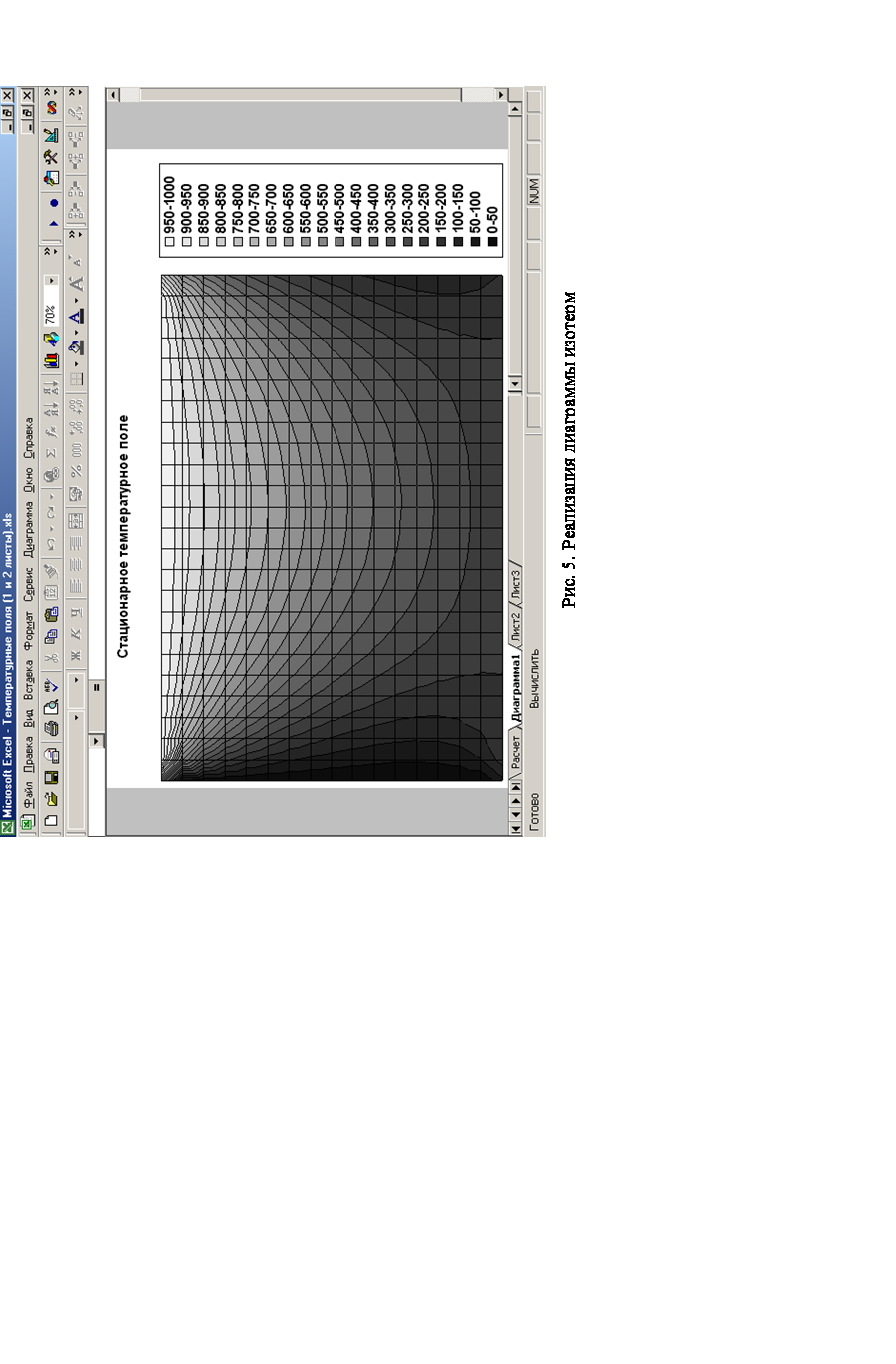
Для графического анализа полученных результатов создается диаграмма типа Поверхность (вариант построения линий уровня).
Пример реализации рассмотренной математической модели (экранная форма) приведен на рис. 4, а реализация диаграммы линий уровня температуры приведена на рис. 5.
Порядок выполнения работы
1. По указанию преподавателя выбрать соответствующий вариант задания по таблице 2.
2. Исследовать влияние коэффициентов теплоотдачи на границах прямоугольного сечения и температур греющих и охлаждающих сред на перепад температуры по всему сечению.
3. Построить регрессионную зависимость перепада температуры по сечению от коэффициентов теплоотдачи при средних значениях температур греющих и охлаждающих сред и регрессионную зависимость перепада температуры от температур греющих и охлаждающих сред при средних значениях коэффициентов теплоотдачи с помощью статистического пакета Excel.
4. Сделать выводы.
Оформление отчета
Отчет оформляется индивидуально каждым студентом, и должен содержать краткие теоретические сведения и результаты по соответствующим пунктам.
Таблица 2
Исходные данные для выполнения работы (на всех границах задаются граничные условия III рода)
|
Вариант задания |
Диапазон изменения коэффициентов теплоотдачи, Вт/(м2·°С) |
Диапазон изменения температур греющих (охлаждающих) сред, 0С |
Вид материала, коэффициент теплопроводности, Вт/(м·°С) |
|
1 |
a1 = 10 ¸ 20 a2 = 100 ¸ 150 a3 = 50 ¸ 60 a4 = 400 ¸ 500 |
t1 = 100 ¸ 200 t2 = 400 ¸ 500 t3 = 5 ¸ 10 t4 = 1000 ¸ 1500 |
Медь 384 |
|
2 |
a1 = 300 ¸ 400 a2 = 40 ¸ 100 a3 = 5500 ¸ 6000 a4 = 100 ¸ 110 |
t1 = 1000 ¸ 1100 t2 = 40 ¸ 50 t3 = 500 ¸ 520 t4 = 100 ¸ 160 |
Сталь 60 |
|
3 |
a1 = 10 ¸ 24 a2 = 400 ¸ 420 a3 = 120 ¸ 140 a4 = 1000 ¸ 1200 |
t1 = 400 ¸ 600 t2 = 40 ¸ 50 t3 = 500 ¸ 520 t4 = 100 ¸ 160 |
Шамот 1,1 |
|
4 |
a1 = 1000 ¸ 1100 a2 = 400 ¸ 500 a3 = 10 ¸ 28 a4 = 160 ¸ 320 |
t1 = 100 ¸ 130 t2 = 340 ¸ 450 t3 = 200 ¸ 300 t4 = 1000 ¸ 1600 |
Кирпич 0,25 |
|
5 |
a1 = 500 ¸ 600 a2 = 320 ¸ 420 a3 = 400 ¸ 600 a4 = 100 ¸ 200 |
t1 = 1000 ¸ 1500 t2 = 800 ¸ 1000 t3 = 1000 ¸ 1300 t4 = 340 ¸ 540 |
Алюминий 204 |
Лабораторная
работа №3
Исследование кинетики Гетерогенных химических реакций.
Теоретические сведения
При производстве металла в сталеплавильных агрегатах, где применяют для продувки ванн, с помощью специальных фурм, практически чистый кислород, значительную роль в окислительных процессах играют гетерогенные реакции взаимодействия примесей чугуна с оксидами железа. Эти реакции протекают в две стадии [2]. На первой стадии за счет кислорода дутья образуются оксиды железа
2Fe + O2 = 2FeO.(28)
Затем оксиды, внедряясь в металл, взаимодействуют с примесями по реакциям
[C] + (FeO) = {CO} + [Fe]
[Si] + 2(FeO) = (SiO2) + 2[Fe]. (29)
[Mn] + (FeO) = (MnO) + [Fe]
Оставшаяся часть оксидов поступает в шлак. Окисление компонентов чугуна за счет оксидов железа называют косвенным окислением. Наряду с окислением происходит также и прямое, т.е. окисление элементов непосредственно кислородом дутья.
В данной работе рассмотрим задачу моделирования и исследования кинетики косвенного окисления примесей. Математическое описание механизма реакций (28) и (29) получим на основе следующих предположений [3].
В соответствии с уравнением реакции (28) скорость образования оксидов железа определяется интенсивностью подвода кислорода
, (30)
где a - степень использования кислорода;
- интенсивность
подачи кислорода к месту реакции, моль/с.
Образующиеся оксиды железа согласно уравнениям (29) расходуются на окисление примесей со скоростью
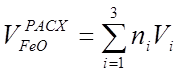, (31)
где ni - стехиометрические коэффициенты при FeO в уравнениях (29);
Vi - скоростьi- ой реакции.
Следовательно, на основе закона сохранения вещества скорость изменения количества оксидов железа в шлаке будет определяться выражением
. (32)
Подставив уравнение (30) и (31) в уравнение (32) получим дифференциальное уравнение, описывающее закон изменения количества молей оксидов железа в шлаке
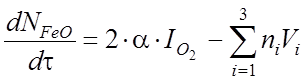. (33)
Скорость любой реакции вида (29), без учета взаимного влияния примесей на механизм перераспределения кислорода между ними и термодинамических границ и условий протекания процессов, можно описать следующим уравнением:
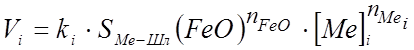, (34)
где ki - константа скорости i – ой реакции;
SМе-Шл - поверхность контакта металла со шлаком;
- порядок реакции по (FeO) и [Me]i;
[Me]i - концентрация i-го элемента в металле.
С целью упрощения модели величины масс металла и шлака примем постоянными так, что mШл / mMe = const = qШл; концентрации элементов выразим через проценты по массе; скорость – через %/мин., а интенсивность подачи кислорода – м3/(т×мин.). Тогда получим исходную систему уравнений
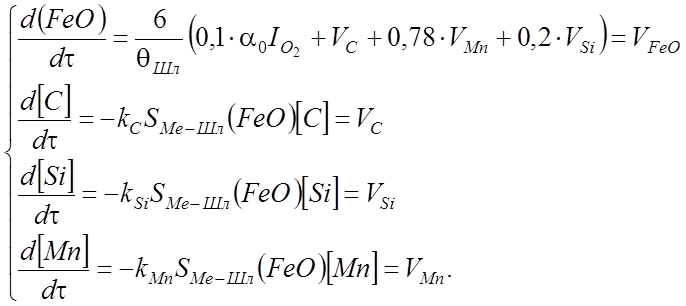(35)
При этом в системе (35) для каждого уравнения дано обозначение правой части, являющейся скоростью изменения концентрации соответствующего вещества.
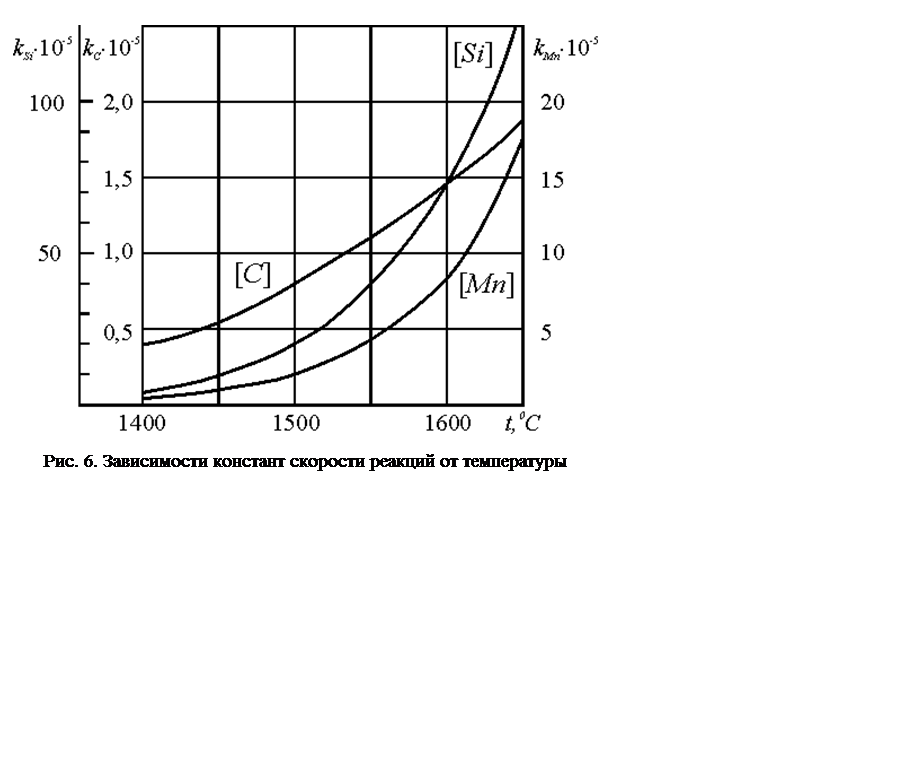
Зависимость констант скорости i – ой реакции от
температуры приведена на рис. 6.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.