Исследование физико-химических процессов с использованием ЭВМ на основе табличного процессора Excel: Методические указания к выполнению лабораторно-практических работ, страница 3

Заполнение именованных ячеек. Для параметров t_ср, b₁, b₂,…, b_N, Dt в соответствующих именованных ячейках вводятся их значения согласно варианту поставленной задачи моделирования и конечно-разностной аппроксимации. Для параметров x₁, x₂ ,…, x_N  вводятся соответствующие формулы для их расчета.

Реализация конечно-разностных соотношений.

В выбранном диапазоне ячеек реализуются формулы либо (10), либо (12), либо (14) в зависимости от выбранной конечно-разностной схемы. Динамику изменения времени и температур слоев во времени целесообразно расположить в ячейках соседних столбцов (формулы для расчета значения времени расположить в первом самом левом столбце) столбцов сверху вниз, при этом в верхней строке диапазона расположить начальные значения времени и температур слоев стенки.

Например, в случае использования явной конечно-разностной схемы во всех ячейках столбца для расчета температуры первого слоя, нагревающегося от внешней среды, вводится формула на основе соотношения (10)

,

а в ячейках столбцов для расчета температуры второго и последующего слоев, нагревающихся от предыдущего слоя, вводятся формулы

,

 и т. д.

Формулы, набранные в верхней строке выбранного диапазона далее копируются вниз на необходимое количество ячеек в зависимости от требуемого времени нагрева многослойной стенки.

Далее для графического анализа полученных результатов создается диаграмма. При этом можно создать либо внедренную в рабочий лист диаграмму, либо отдельный лист диаграммы. Для этого выполните следующие операции:

1.  Выделите ячейки, содержащие данные, которые должны быть отражены на диаграмме.

2.  Чтобы заголовок столбца или строки для новых данных появился в диаграмме, в выбираемые ячейки нужно включить те, которые содержат этот заголовок.

3.  Нажмите кнопку Мастер диаграмм.

4.  Следуйте инструкциям мастера диаграмм. При выполнении данной лабораторной работы следует диаграмму типа Точечная либо с маркерами на графиках, либо без них.

Пример реализации рассмотренной математической модели (экранная форма) приведен на рис. 2.

Порядок выполнения работы

1.  По указанию преподавателя выбрать соответствующий вариант задания по таблице 1.

2.  Исследовать влияние температуры греющей среды на продолжительность нагрева пластин при средних значениях коэффициента теплоот-

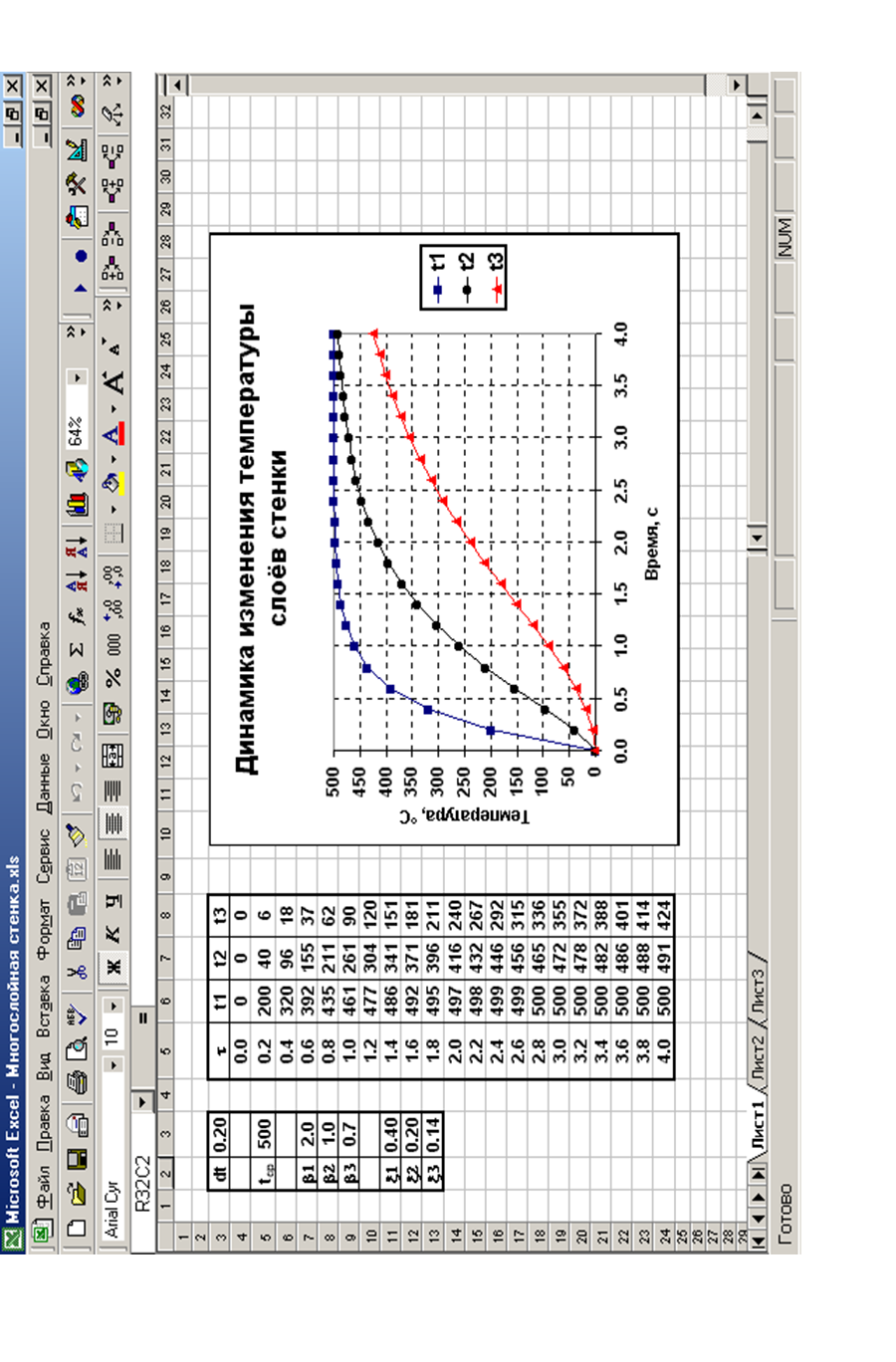
Таблица 1

Исходные данные для выполнения работы

Вариант задания	Количество пластин	Диапазон изменения греющей среды	Диапазон изменения коэффициентов теплопередачи Вт/(м2×град)	Материал	Плотность материалов слоев, кг/м3	Удельная теплоемкость материала слоев Дж/(кг×град)	Толщина пластин, м	Тип конечно-разностной схемы
1	3	1400¸1600	1300¸3000	сталь бронза медь	7900 8000 8800	462 381 381	0,005 0,001 0,004	Неявная
2	2	650¸1100	500¸1000	сталь медь	7900 8800	462 381	0,001 0,005	Кранка-Николсона
3	3	500¸900	140¸300	сталь медь алюминий	7900 8800 2670	462 381 920	0,0005 0,001 0,002	Явная
4	2	1000¸1500	600¸800	сталь алюминий	7900 2670	462 920	0,001 0,003	Кранка-Николсона
5	2	800¸1200	500¸850	сталь бронза	7900 8000	462 381	0,001 0,002	Неявная

дачи. Построить графики зависимостей времени нагрева пластин от температуры греющей среды.

3.  Исследовать влияние коэффициента теплоотдачи на продолжительность нагрева пластин при среднем значении температуры греющей среды. Построить графики зависимостей времени нагрева пластин от коэффициента теплоотдачи .

4.  Сделать выводы.

Оформление отчета

Отчет оформляется индивидуально каждым студентом, и должен содержать краткие теоретические сведения и результаты по соответствующим пунктам.

Лабораторная работа №2

Исследование стационарных температурных
 полей в двумерном приближении

Теоретические сведения

В работе исследуются установившиеся температурные поля в сечении тела прямоугольной формы в зависимости от теплофизических свойств материала тела и граничных условий.

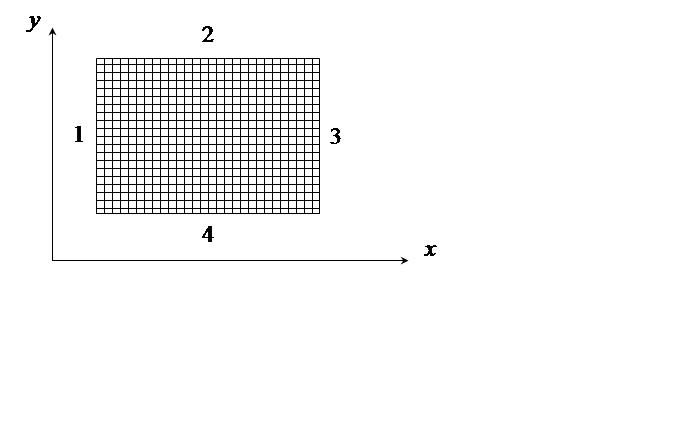
В динамике распространение тепла описывается с помощью уравнения теплопроводности и соответствующих краевых условий, описывающих обмен теплом с окружающей средой с учетом геометрии рассматриваемой области (на рис. 3. цифрами указаны номера границ):

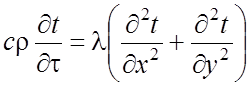,                                                   (15)

где   c  -   удельная теплоемкость материала тела, Дж/(кг·°С) ; r - плотность материала, кг/м³; l - коэффициент теплопроводности материала, Вт/(м·°С).

На 1-ой, 2-ой,  3-ей и 4-ой границах краевые условия задаются следующим образом:

·  условия I рода имеют соответственно номеру границы вид

t = t₁ , t = t₂ , t = t₃ , t = t₄,                                            (16)

где   t₁, t₂, t₃, t₄  -   температуры окружающей среды со стороны соответствующих границ, °С;

Рис. 3. Покрытие исходной геометрической области равномерной по x с шагом Dx и равномерной по y с шагом Dy сеткой

·  условия II рода имеют соответственно вид

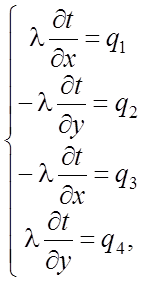                                                                   (17)

где q₁, q₂, q₃, q₄-     значения плотностей тепловых потоков вдоль направления нормалей к соответствующим границам, Вт/м²;

·  условия III рода имеют соответственно вид

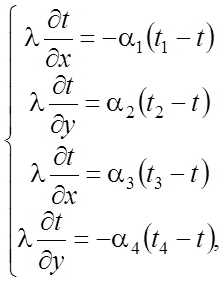                                                        (18)

где a₁, a₂, a₃, a₄ - коэффициенты теплоотдачи со стороны окружающей среды на соответствующих границах, Вт/(м²·°С).

Реализация алгоритма решения задачи моделирования.

Начальный этап.

Для исследования стационарных (установившихся) температурных полей используется дифференциальное уравнение

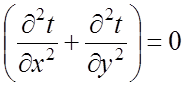,                                                            (19)

которое получено из (15) при 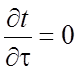с теми же краевыми условиями.