Перейдем к конечно-разностной аппроксимации этого уравнения, заменив производные их конечно-разностным аналогом в виде системы соотношений применительно к узлам сеточной области, как показано на рис. 3.
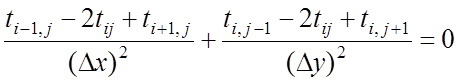, (20)
где Dx, Dy - интервалы дискретизации пространства вдоль декартовых координатных осей Ox и Oy соответственно, определяющие количество интервалов дискретизации (соответственно N и M) по исходным размерам рассматриваемого прямоугольного сечения.
Перепишем полученные соотношения (20) в виде
, (21)
где 
,
; 
;
.
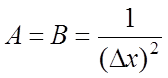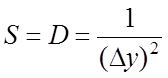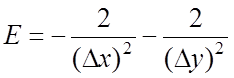Полученные соотношения представляют собой систему линейных
уравнений относительно искомых значений температуры 
в
узлах прямоугольной сетки, показанной на рис. 3. Индекс i нумерует
узлы сетки вдоль оси Ox от 0 до N (указанные значения соответствуют
границе области вдоль направления оси Ox ). Индекс j нумерует
узлы сетки вдоль оси Oy от
0 до M (указанные
значения соответствуют границе области вдоль направления оси Oy ). Полученную систему линейных
уравнений решаем итерационным методом Гаусса-Зейделя с помощью соотношения
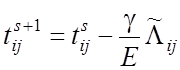, (22)
где 
,
s – номер итерации, 
-
параметр верхней релаксации в методе Гаусса-Зейделя.
Соотношение (22) используется для расчета значений температуры во внутренних узлах сеточной области. При этом на каждой итерации пересчитываются значения искомой температуры во всех граничных узлах с помощью следующих конечно-разностных соотношений, аппроксимирующих те или иные краевые условия на соответствующей границе:
· для граничных условий I рода (2.2):
на 1-ой границе: 
, 
;
на 2-ой: 
, 
; (23)
на 3-ей: 
, ;
на 4-ой: 
, ;
· граничные условия II рода (17) аппроксимируются с помощью конечных разностей на 1-ой, 2-ой и т.д. границах с помощью соотношений:
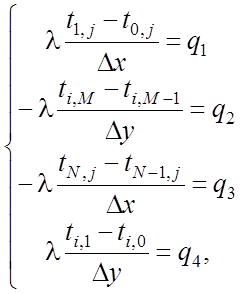(24)
на основе которых получаются следующие алгоритмические соотношения для вычисления температуры в граничных узлах:
на 1-ой границе: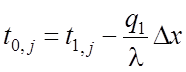 
, ;
на 2-ой: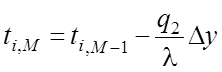 
, ;
(25)
на 3-ей: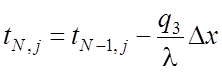 
, ;
на 4-ой: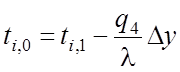 
, ;
· граничные условия II рода (2.4) аппроксимируются с помощью конечных разностей на 1-ой, 2-ой и т.д. границах с помощью соотношений:
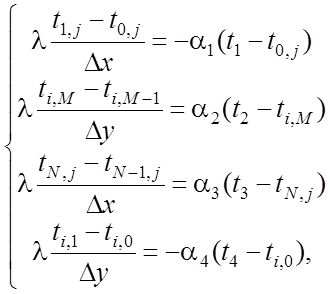(26)
на основе которых получаются следующие алгоритмические соотношения для вычисления температуры в граничных узлах:
на 1-ой границе: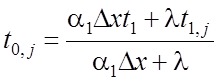 
, ;
на 2-ой: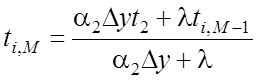 
, ;
(27)
на 3-ей: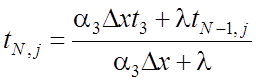 
, ;
на 4-ой: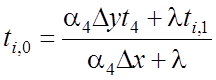 
, .
При этом в угловых узлах расчетной области реализуется расчетная формула для среднего значения температур в прилегающих граничных узлах, не являющихся угловыми.
Основной этап.
Выбор параметров задачи. Параметрами задачи являются следующие из ниже перечисленных: l, t1, t2, t3, t4, q1, q2, q3, q4, a1, a2, a3, a4, Dx, Dy, g. Кроме этого целесообразно выделить такие параметры конечно-разностного оператора как A,B,S,D,E.
Создание именованных ячеек. Для выбранных выше параметров формируются соответствующие ячейки с именами соответственно lambda, T1, T2, T3, T4, q1, q2, q3, q4, alfa1, alfa2, alfa3, alfa4, dx, dy, gamma, A, B, S, D, E, в соседних ячейках с которыми с которыми дается обозначение либо комментарий соответствующего параметра.
Заполнение именованных ячеек. Для параметров l, t1, t2, t3, t4, q1, q2, q3, q4, a1, a2, a3, a4, Dx, Dy, g в соответствующих именованных ячейках вводятся их значения согласно поставленной задачи моделирования и конечноразностной аппроксимации. Для параметров A,B,S,D,E вводятся соответствующие формулы для их расчета.
Реализация конечно-разностных соотношений.
Так как в задаче используется итерационный алгоритм для расчета температурного поля, то необходимо предварительно обеспечить возможность итерационных вычислений, при этом лист будет пересчитываться столько раз, какое значение указано в поле Предельное число итераций, или когда все величины модели изменятся за одну итерацию на число, меньшее указанного в поле Относительная погрешность. Возможность итерационных вычислений обеспечивается следующим образом:
1. В меню Сервис выберите пункт Параметры и перейдите на вкладку Вычисления.
2. Установите флажок Итерации.
3. Далее можно ввести количество итераций, выполняемых при обработке формул в поле Предельное число итераций. Чем больше предельное число итераций, тем больше времени потребуется для пересчета листа. Однако для отладки вновь созданной задачи в ручном режиме введите количество итераций, равное 1.
4. Введите относительную погрешность вычислений в поле Относительная погрешность. Чем меньше погрешность, тем больше время пересчета листа и точнее результаты обработки формул.
5. Переключатель способа пересчета листа установите в положение Вручную для обеспечения возможности отладки вновь созданной задачи. Пересчет рабочего листа осуществляется с помощью кнопки F9.
В диапазоне ячеек, отведенном для реализации конечно-разностных соотношений во внутренних узлах рассматриваемой области, вводится формула
,
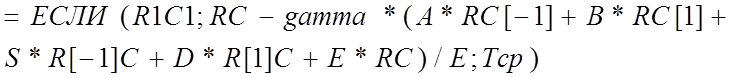где Tср - имя ячейки с оценочным средним значением ожидаемого температурного поля (вводится для уменьшения количества итераций).
В приведенной реализации предполагается , что в ячейке R1С1 находится управляемое с помощью флажка логическое значение, позволяющее переключать алгоритмы расчета в ячейках с одного на другой (в данном случае с основного алгоритма на значение средней температуры окружающей среды, хранящееся в именованной ячейке с именем Tср) и проводить серию расчетов в вычислительном эксперименте. Вставка флажка в удобном месте рабочего листа осуществляется с помощью команды «Флажок» (панель «Формы»)
В ячейках, соответствующих первой границе, вводится, например для случая граничных условий III рода, формула
,
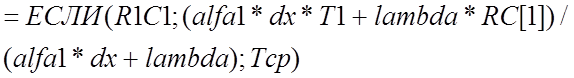Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.