Исследование физико-химических процессов с использованием ЭВМ на основе табличного процессора Excel: Методические указания к выполнению лабораторно-практических работ, страница 2

2.4.  Реализация конечно-разностных соотношений на выбранном диапазоне ячеек, соответствующем пространственно-временной области, в которой рассматривается исходная математическая модель, с учетом начальных и краевых условий, путем введения в ячейки формул, соответствующих этим соотношениям. Как правило, получающиеся длинные формулы достаточно набрать один раз, а потом скопировать их в нужный диапазон ячеек, а при наборе стараться как можно меньше пользоваться текстовым редактором, а использовать левую кнопку мыши персонального компьютера для активизации того или иного адреса либо имени ячейки для использования их в формуле.

2.5.  Для визуального удобства применить для диапазонов ячеек как с параметрами модели, так и с расчетными формулами, обозначение границ диапазонов, заливку их тем или иным цветом, изменение цвета шрифта, расположение надписей в ячейках и значений исходных и искомых параметров по центру ячейки и т.д. с помощью стандартных средств Excel.

3.  Заключительный этап. Получение графических результатов, их анализ и физико-химическая интерпретация. Проведение серии вычислительных экспериментов.

Лабораторная работа №1
Исследование нагрева многослойной стенки

Теоретические сведения

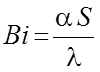
Нагрев любого тела происходит в два этапа, которые включают передачу тепла из окружающей среды на поверхность материала и распространение тепла в его объеме. Соотношение между количеством тепла, полученным поверхностью, и количеством тепла, отведенным внутрь тела, определяется критерием Био [1]:

                                                                         (1)

где   a          -   коэффициент теплоотдачи на поверхность тела, Вт/(м²×град);

        S          -   толщина тела, м;

        l          -   коэффициент теплопроводности материала, Вт/(м×град).

Если процесс теплоотдачи на поверхность происходит интенсивнее передачи тепла внутрь тела (Bi ³ 0,5), то будет иметь место градиент температуры по сечению. Поэтому температура любой точки тела будет зависеть от ее пространственного расположения, т.е. является функцией координаты и времени, что обуславливает необходимость описания механизма нагрева с помощью дифференциальных уравнений в частных производных.

В настоящей работе рассмотрим задачу нагрева теплотехнических “тонких” тел, разделенных воздушной прослойкой (рис. 1), для которых Bi <0,25, что характеризует интенсивный отвод тепла внутрь тела, поэтому разность температур по сечению оказывается незначительной и ей можно пренебречь. На основании изложенных предпосылок, получим определяющее дифференциальное уравнение, описывающее нагрев тонкого тела.

Количество тепла dQ, воспринимаемого поверхностью F от греющей среды с температурой t_ср за время dt, равно:

.(2)

Это количество тепла расходуется на изменение энтальпии нагреваемого тела массой m с удельной теплоемкостью с

.(3)

После преобразования получаем

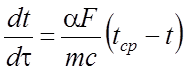.                                                              (4)

Соотношение  преобразуется к виду , где k – коэффициент формы (для пластины k = 1, цилиндра и фара соответственно k = 2 и k = 3),
r - плотность тела, кг/м³.

Тогда уравнение (4) применительно к описанию нагрева пластины преобразуется к виду

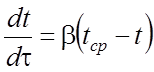,                                                                   (5)

где 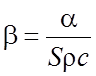, 1/с.

Для нашего случая (рис. 1) изменение температуры первой пластины в соответствии с уравнением (5) будет подчиняться закону

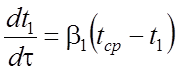.                                                                (6)

Изменение температуры второй пластины за счет температуры первой пластины, без учета тепловых потерь, можно описать следующим уравнением

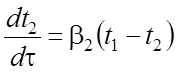.                                                                (7)

Систему уравнений (6), (7) можно распространить для произвольного количества N пластин, разделенных между собой воздушными прослойками.

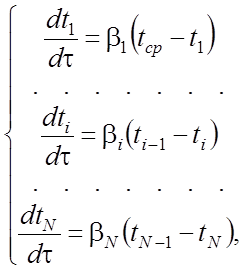                                                       (8)

где   i   -   номер пластины, b_i - соответствующий коэффициент температуропроводности.

Такое соединение пластин часто используют при создании тепловых экранов.

Цель работы: приобретение практических навыков моделирования  механизма нагрева многослойной стенки с использованием табличного процессора Excel и исследование влияния температуры греющей среды, а также параметров процесса на динамику нагрева пластин.

Реализация алгоритма решения задачи моделирования.

Начальный этап.

С помощью конечно-разностной аппроксимации перейдем от системы (8) дифференциальных уравнений к системе алгебраических уравнений. При этом используем три варианта конечно-разностной схемы: явную, неявную и Кранка-Николсона. После применения явной конечно-разностной схемы получается система уравнений

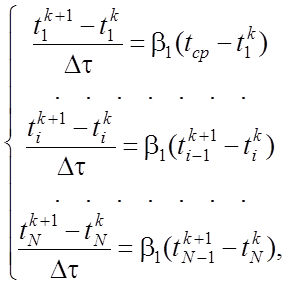                                                 (9)

где   k  -   номер шага по времени с шагом интегрирования Dt, а  - значение температуры i-ого слоя на k-ом шаге.

После преобразования системы (9) к виду, позволяющему вычислять последующие значения температуры через предыдущие, получается система соотношений

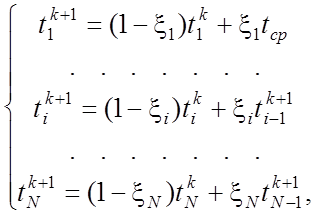                                           (10)

где x_i = Dtb_i.

После применения неявной конечно-разностной схемы получается система уравнений

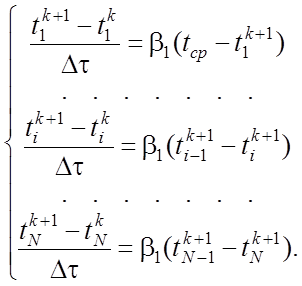                                             (11)

После преобразования системы (11) к явному виду для вычисления последующих значений температуры через предыдущие, получается система соотношений

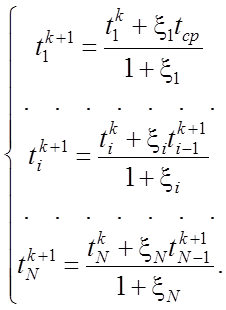                                                        (12)

После применения конечно-разностной схемы Кранка-Николсона получается система уравнений

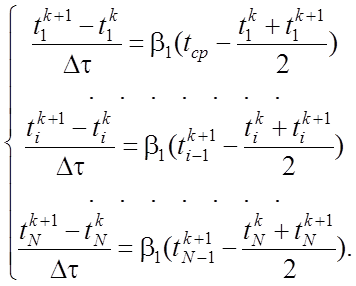                                     (13)

После преобразования системы (13) к явному виду для вычисления последующих значений температуры через предыдущие, получается система соотношений

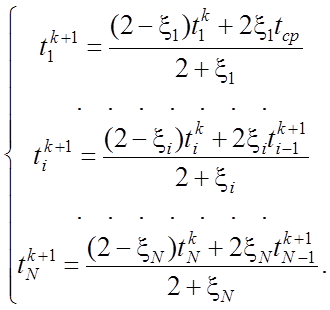                                         (14)

Основной этап.

Выбор параметров задачи.    Параметрами задачи являются следующие из ниже перечисленных: t_ср, b₁, b₂,…, b_N, Dt. Кроме этого целесообразно выделить такие параметры конечно-разностных операторов как x₁, x₂ ,…, x_N.

Создание именованных ячеек. Для выбранных выше параметров формируются соответствующие ячейки с именами соответственно Tср, betta1, betta2,…, bettaN, dt, ksi1, ksi2,…, ksiN, в соседних ячейках с которыми с которыми  дается обозначение либо комментарий соответствующего параметра.