-.413E+00 -.555E+00 -.413E+00 -.452E+00 .827E+01
КОBАРИЦИОННАЯ МАТРИЦА КОЭФФИЦИЕНТОВ
.325E-02
.117E-02 .359E-02
.641E-03 .439E-03 .326E-02
-.311E-04 -.346E-03 .199E-02 .604E-02
-.221E-01 -.297E-01 -.221E-01 -.242E-01 .443E+00
ОЦЕНКИ КОЭФФИЦИЕНТОВ .40226 .45908 .26856 .36879 -.71404E-01
Y2 = 0.40226*X1+0.45908*X2+0.26856*U1+0.36879*U2-0.71404E-0.1
Для Y1:
ЧИСЛО НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ K= 4
OБЪEM ВЫБОРКИ N= 21
ИСХОДНЫЕ ДАННЫЕ:X1,X2,Y1
ТАБЛИЧНОЕ ЗНАЧЕНИЕ Т-КРИТЕРИЯ TKR= 2.086
ТАБЛИЦА HOMEPOB ИССЛЕДУЕМЫХ ФУНКЦИЙ
1 I 1
2 I 2
3 I 3
4 I 4
ДИСПЕРСИЯ Y= .815025E+00
ПАРАМЕТРЫ СТАНДАРТИЗАЦИИ XM И SX
1 .37067E+01 .98056E+00
2 .70286E+01 .92789E+00
3 .30133E+01 .10481E+01
4 .34286E+01 .75484E+00
ЭЛЕМЕНТЫ КОРРЕЛЯЦИОННОЙ МАТРИЦЫ
.100E+01
-.315E+00 .100E+01
-.175E+00 -.115E+00 .100E+01
.649E-01 .121E+00 -.468E+00 .100E+01
ЧИСЛО ОБУСЛОВЛЕННОСТИ МАТРИЦЫ V= .133742E+01
! ФУНКЦИИ,ВКЛЮЧЕННЫЕ В РЕГРЕС- ! ЗНАЧ.ПАРАМЕТРА ! ЗНАЧ. !
! СИОННОЕ УРАВНЕНИЕ ! РЕГРЕССИИ ! T-КРИТЕРИЯ !
! ! ! !
! 1 ! .7909194E+00 ! 6.581 !
! 2 ! -.3632922E-01 ! .304 !
! 3 ! .5763851E+00 ! 4.483 !
! 4 ! .9153012E-01 ! .726 !
НОМЕР НЕЗНАЧИМОГО КОЭФФИЦИЕНТА 2
ЧИСЛО ОБУСЛОВЛЕННОСТИ МАТРИЦЫ V= .131530E+01
! ФУНКЦИИ,ВКЛЮЧЕННЫЕ В РЕГРЕС- ! ЗНАЧ.ПАРАМЕТРА ! ЗНАЧ. !
! СИОННОЕ УРАВНЕНИЕ ! РЕГРЕССИИ ! T-КРИТЕРИЯ !
! ! ! !
! 1 ! .8034211E+00 ! 7.300 !
! 3 ! .5814147E+00 ! 4.679 !
! 4 ! .8867975E-01 ! .723 !
НОМЕР НЕЗНАЧИМОГО КОЭФФИЦИЕНТА 4
ЧИСЛО ОБУСЛОВЛЕННОСТИ МАТРИЦЫ V= .103167E+01
! ФУНКЦИИ,ВКЛЮЧЕННЫЕ В РЕГРЕС- ! ЗНАЧ.ПАРАМЕТРА ! ЗНАЧ. !
! СИОННОЕ УРАВНЕНИЕ ! РЕГРЕССИИ ! T-КРИТЕРИЯ !
! ! ! !
! 1 ! .8018593E+00 ! 7.380 !
! 3 ! .5396756E+00 ! 4.967 !
ОСТАТОЧНАЯ ДИСПЕРСИЯ= .186517E+00
ОСТАТОЧНАЯ СУММА КВАДРАТОВ= .35438E+01
ОТНОШЕНИЕ ДИСПЕРСИЙ F= .22885
КОЭФФИЦИЕНТ МНОЖЕСТВЕННОЙ КОРРЕЛЯЦИИ = .885
GAMMA= 2.09
КОЭФФИЦИЕНТЫ МОДЕЛИ В НАТУРАЛЬНОМ МАСШТАБЕ
B( 1)= .738262E+00 B( 2)= .000000E+00 B( 3)= .464866E+00 B( 4)= .000000E+00
B( 5)= .152238E+00
----------------------------------------------------------
----------------------------------------------------------
ДИСПЕРСИОННАЯ МАТРИЦА ПЛАНА
.536E-01
.879E-02 .470E-01
-.225E+00 -.174E+00 .141E+01
КОBАРИЦИОННАЯ МАТРИЦА КОЭФФИЦИЕНТОВ
.100E-01
.164E-02 .876E-02
-.420E-01 -.325E-01 .263E+00
ОЦЕНКИ КОЭФФИЦИЕНТОВ .73826 .46487 .15224
Y1=0.73826*X1+0.46457*U1+0.15224
Постановка задачи оптимизации ТОУ и ее решение.
(решение всех задач оптимизации выполнено при помощи программы Mathсad 11. Текст программы находится в файле optim.mcd )
В технологическом процессе сушки основной целью является минимизация влажности сырья.
В качестве целевой функции выберем параметр Y2, который определяет влажность сырья на выходе объекта.
В качестве функционального ограничения возьмем Y1 – параметр, который определяет температуру сырья на выходе объекта.
Таким образом необходимо определить вектор переменных (X1, X2, U1, U2), при
Y2=0.40226 X1+ 0.45908 X2+ 0.26856 U1+ 0.36879 U2+ 0.0714→ min
Y1=0.73826 X1 + 0.46457 U1 + 0.15224
1 ≤ X1 ≤ 5.2
5≤ X2 ≤ 9
1 ≤ U1 ≤ 5
2 ≤ U2 ≤ 5
Функциональное ограничение :
Y1=0.73826 X1 + 0.46457 U1 + 0.15224→ min
1 ≤ X1 ≤ 5.2
5≤ X2 ≤ 9
1 ≤ U1 ≤ 5
2 ≤ U2 ≤ 5
Решение: Y1min = 1.355 при (X1, X2, U1, U2)=( 1 , 5.2 , 1 , 5 )
Y1=0.73826 X1 + 0.46457 U1 + 0.15224→ max
1 ≤ X1 ≤ 5.2
5≤ X2 ≤ 9
1 ≤ U1 ≤ 5
2 ≤ U2 ≤ 5
Решение: Y1max = 6,314 при (X1, X2, U1, U2)=( 5.2 , 5.2 , 5 , 5 )
Постановка стохастической задачи оптимизации
Т.к. выход значений Y1 за допустимые границы, рассчитанные выше , приводит к существенным потерям, то задачу стохастической оптимизации формулируется в виде Р - модели:
Y2(X1, X2, U1, U2)®min
1 ≤ X1 ≤ 5.2
5≤ X2 ≤ 9
1 ≤ U1 ≤ 5
2 ≤ U2 ≤ 5
P [ Y2(X1, X2, U1, U2) £ Y2max ] ³ p
P [ Y2(X1, X2, U1, U2) ³ Y2min ] ³ p, где
p = 0.9 – доверительная вероятность
1. Искусственное сведение стохастической задачи к детерминированной
Y2=0.40226 X1+ 0.45908 X2+ 0.26856 U1+ 0.36879 U2+ 0.0714→ min
1 ≤ X1 ≤ 5.2
5≤ X2 ≤ 9
1 ≤ U1 ≤ 5
2 ≤ U2 ≤ 5
Y1min + u[α/2=(1-p)/2]s{ Y1} ≤ Y1(X1, X2, U1, U2)≤ Y1max – u[α/2=(1-p)/2]s{ Y1}
p = 0.9 – доверительная вероятность
u[α/2=(1-p)/2]– квантиль нормированного нормального распределения
α/2=(1-p)/2 => α/2=0.05
u[α/2=(1-p)/2]=1.64
Решение: Y2 = 6.474 при (X1, X2, U1, U2)=( 2.591 , 6.8 , 2.001 , 5 )
2. Исследование чувствительности оптимального решения к ошибкам
Пусть
необходимо решить две задачи: с «широкой» допустимой областью (коэффициенты
ограничений равны ![]() , коэффициенты критерия
равны
, коэффициенты критерия
равны 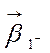 ), и с «узкой» допустимой областью
(коэффициенты ограничений равны
), и с «узкой» допустимой областью
(коэффициенты ограничений равны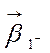 , коэффициенты
критерия равны
, коэффициенты
критерия равны![]() ).
).
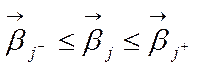 :
:
|
|
|
|
|
|
|
|
|
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.