Информатика и выч. техника \ Автоматизированные информационно-управляющие системы

Анализ и синтез на базе комплекса технических средств гипотетической микропроцессорной системы оптимального управления технологическим процессом и оборудованием технического объекта (Сушка), страница 4

Описание алгоритма– при увеличении значения Y2 (когда Y2>Y2* ) необходимо либо уменьшить значение x1, либо уменьшить значение x2. Аналогично, при уменьшении значения Y2 (когда Y2<Y2*) необходимо либо увеличить значение x1, либо увеличить значение x2. Так как Y2 – непрерывная, а не дискретная величина, то исходя из математических соображений ситуация равенства не рассматривается (практически невозможно достигнуть такой ситуации).   

Режим НЭ. (100chisel.I1)

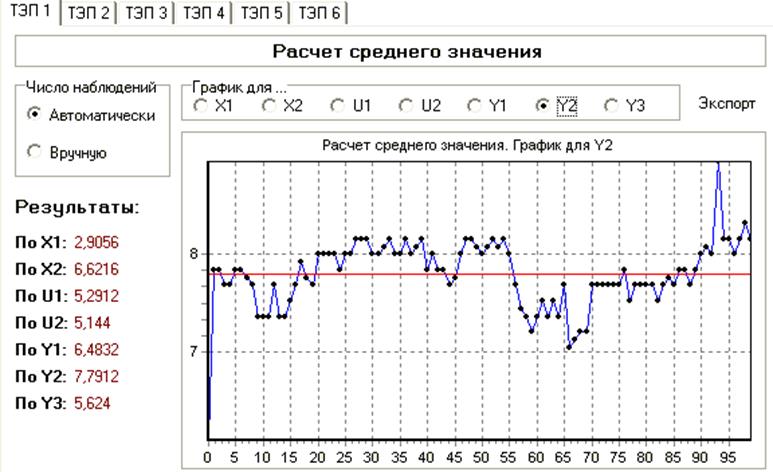
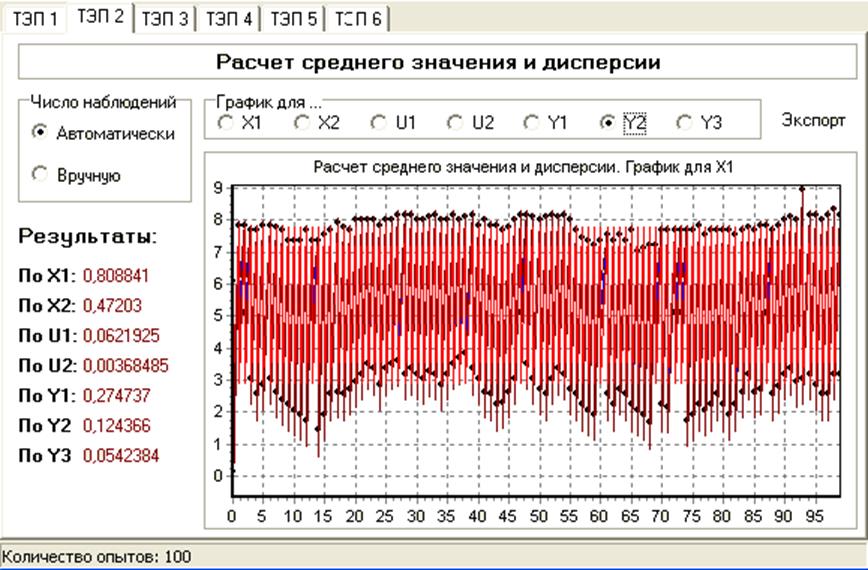
Ручное управление. (Hand.I4)

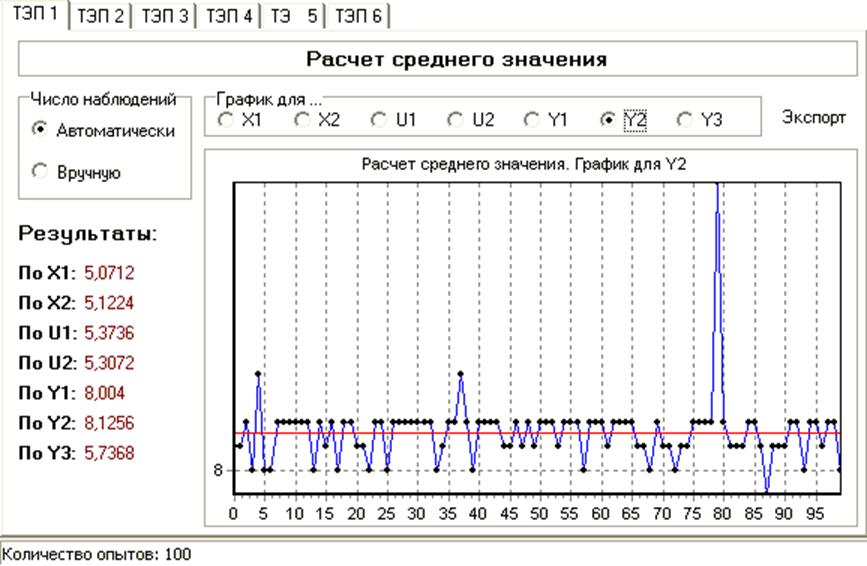
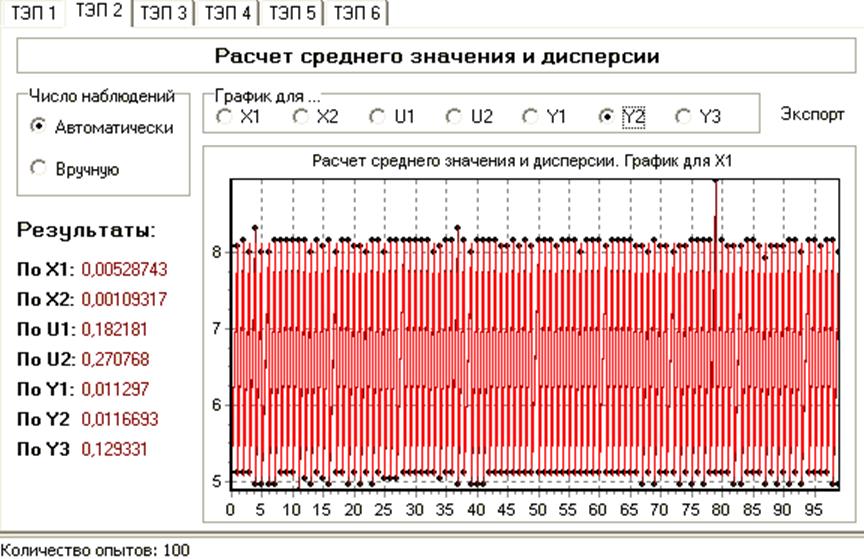
Вывод: из результатов расчетов ТЭП1 и ТЭП2 можно заключить, что режим РУ более эффективен, чем режим НЭ.

Оценивания интервалов корреляции (8punkt.I4)

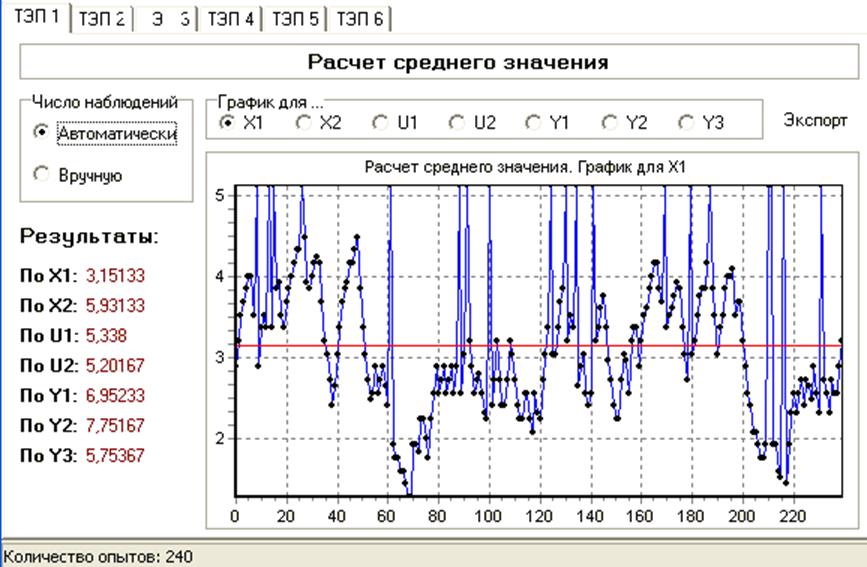
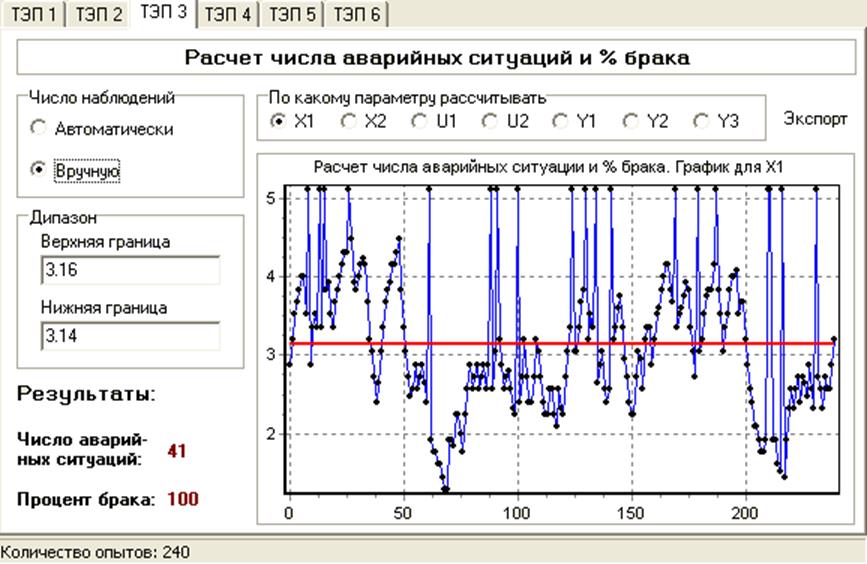
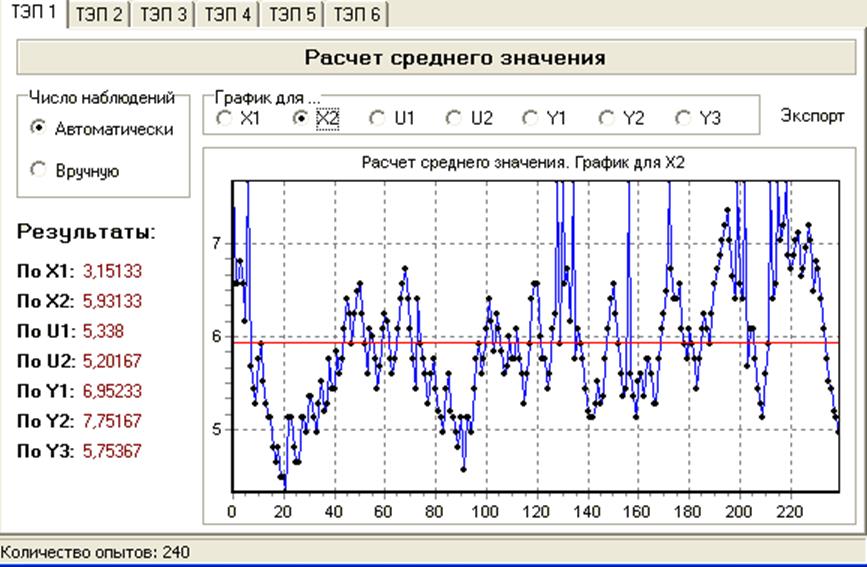
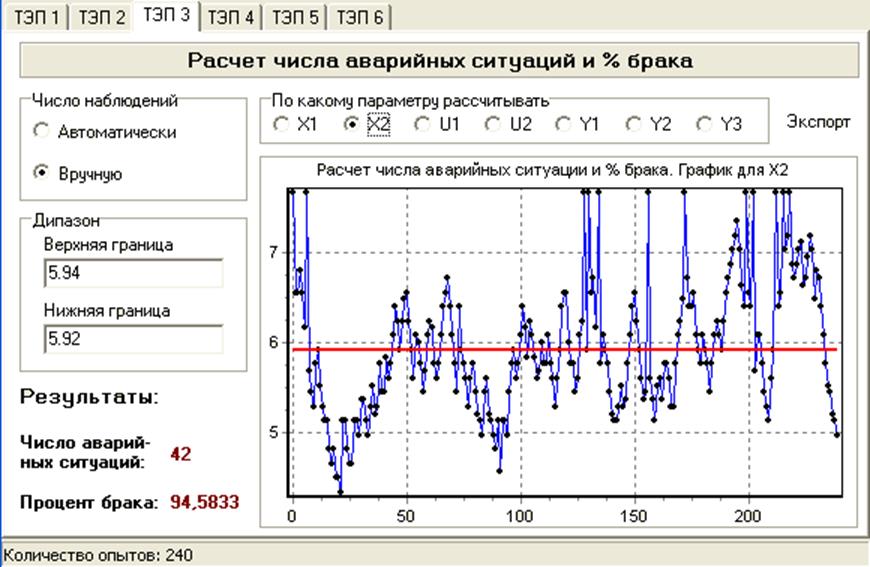
Интервал корреляции может быть грубо оценен через соотношение:

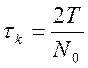
где N0 – число пересечений реализацией x(t) за T время линии, соответствующей среднему значению процесса.

Для X1: N01=41, 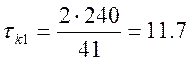c

Для X2: N02=42, 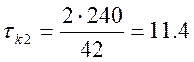c

Число ординат корреляционных функций n = 10

Интервал дискретизации: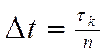

         

         

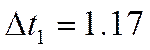
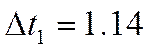
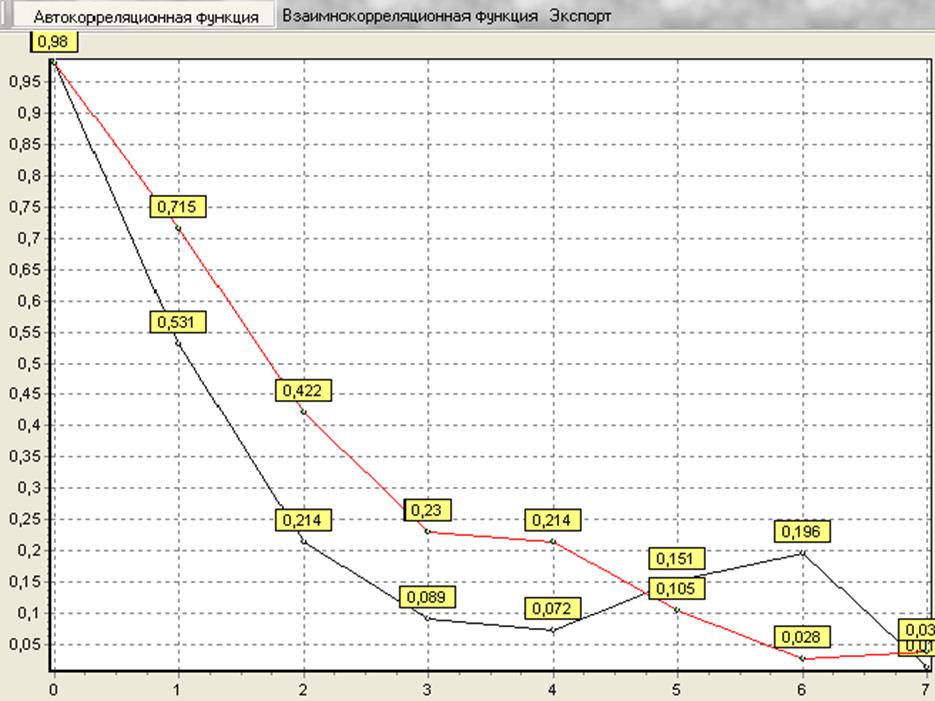
Расчет 10 ординат авто- и  взаимнокорреляционных функций.

Используя КТС и ППО УИК был реализован информационный режим и зарегистрировано 50 значений контролируемых переменных с выбранным раннее шагом дискретизации (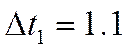).  (punkt 10.I4).

Используя ППО комплекса, рассчитаем значения 10 ординат авто- и взаимнокорреляционных функций контролируемых переменных.

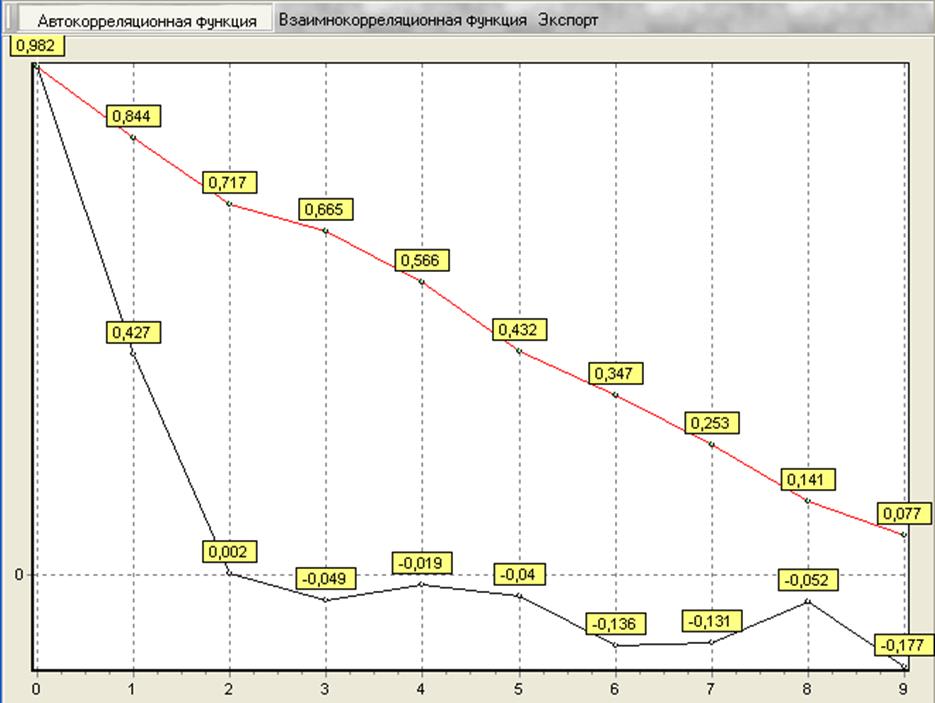
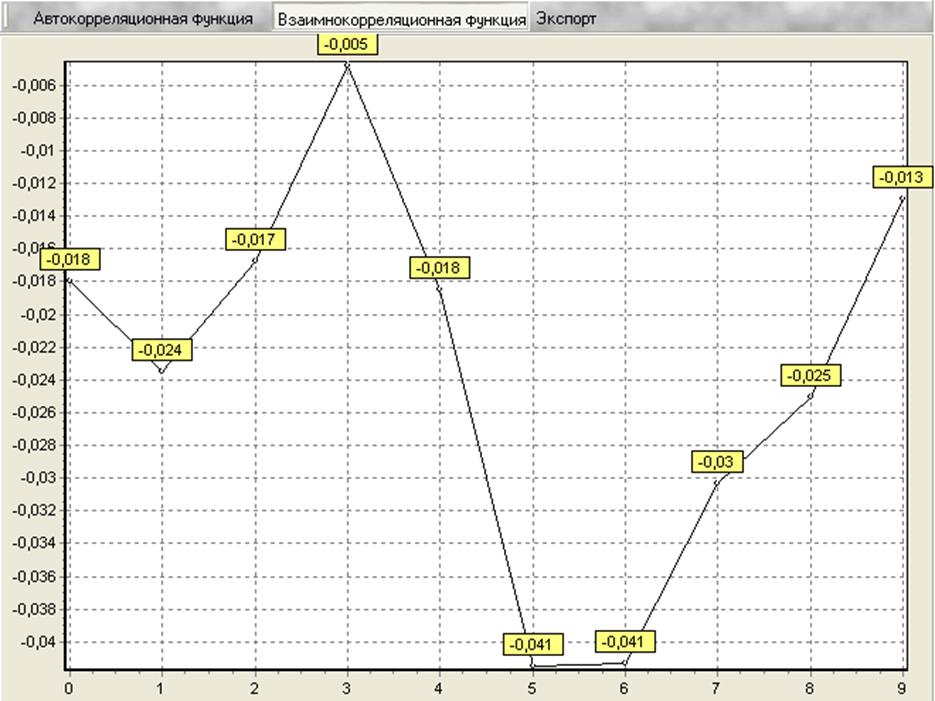
Уточнение шага дискретизации.

Число ординат корреляционных функций n = 9

Интервал корреляции: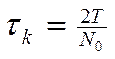

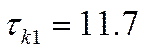
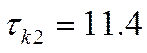
Интервал дискретизации: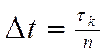

         

         

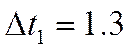
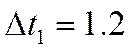
Выбранный с.

Получение регрессионной модели

   Задачи эффективности прогноза и оптимального упавления ,задачи создания АСУТП требуют получения математического описания объектов и процессов ,т.е. их математических моделей .При этом в зависимости от специфики изучаемого технологического процесса его отдельные фазы (агрегаты) могут описываться статистическими или динамическими уравнениями .Для построения модели статического объекта построим регрессионную модель,т.е. получим уравнение описывающее объект:

                                      yi=n(xi,b)+ei,

  где yi-наблюдаемая в i-м опыте выходная переменная; xiT- вектор “k” входных переменных в этом же опыте; ei- значение случайной адитивной помехи, распределенной по нормальному закону; bi-вектор неизвестных коэфициентов; n(xi,b )-некоторая функция.

   Идентификация статических характеристик  ТОУ рекомендовано производить, используя пассивный эксперимент. Он основан на регистрации контролируемых параме­тров процесса в режиме нормальной эксплуатации работы объекта без вне­сения преднамеренных возмущений. Если число опытов в пассивном эксперименте задано (например, из экономических соображений с учетом их стоимости), единственное, что можно сделать для увеличения точности регрессионной модели, это выбрать оптимальным образом интервал съема данных Dt, который опре­деляют из условия получения наиболее близкой к диагональной информационной матрицы с максимальным определителем. Для этого необходимо знать авто- и взаимоковариционные функции случайных процессов X(t) ТОУ В частности, если при любых интервалах корреляции взаимная ковариация между переменными отсутствует, оптимальный выбор должен производиться из условия Dt= maxtkj, j=1,k, где tkj - интервал корреляции (время затухания) процесса Xj(t). т.е интервал Dt между соседними отсчетами должен, быть (больше чем время затухания автокорреляционной функции самого "медленного" случайного процесса. Однако не имеет смысла делать Dt много больше времени т.к, так как при этом продолжительность эксперимента  существенно возрастает, а величины выборочных дисперсий практически не меняются.

   После того как интервал съема данных Dt выбран, осуществляется пас­сивный эксперимент, те. в моменты времени t1, t2,..., tn, разделенные ин­тервалом Dt измеряются N значений входных переменных xj(t) и выходной пе­ременной Y(t). Полученные данные затем используются для нахождения оце­нок регрессионной модели и оценки дисперсии внешнего шума.

  Можно считать регрессионную модель достаточно точной, если множественный коэффициент корреляции  более 0,86.

  Выбираем интервал дискретизации, больший, чем максимальный  из полученных интервалов корреляции, т.е.

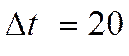
Для Y2:

  ЧИСЛО НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ K= 4
  OБЪEM ВЫБОРКИ N= 21
            ИСХОДНЫЕ ДАННЫЕ:X1,X2,Y1
 
  ТАБЛИЧНОЕ ЗНАЧЕНИЕ Т-КРИТЕРИЯ TKR=  2.086
 
 ТАБЛИЦА HOMEPOB ИССЛЕДУЕМЫХ ФУНКЦИЙ
 
   1 I 1
   2 I 2
   3 I 3
   4 I 4
 
  ДИСПЕРСИЯ Y=  .336640E+00
 
  ПАРАМЕТРЫ СТАНДАРТИЗАЦИИ XM И SX
 
    1  .37067E+01  .98056E+00
    2  .70286E+01  .92789E+00
    3  .30133E+01  .10481E+01
    4  .34286E+01  .75484E+00
 
  ЭЛЕМЕНТЫ КОРРЕЛЯЦИОННОЙ МАТРИЦЫ
 
 
    .100E+01
 
   -.315E+00    .100E+01
 
   -.175E+00   -.115E+00    .100E+01
 
    .649E-01    .121E+00   -.468E+00    .100E+01
 
  ЧИСЛО ОБУСЛОВЛЕННОСТИ МАТРИЦЫ V=  .133742E+01
 
 
 
     ! ФУНКЦИИ,ВКЛЮЧЕННЫЕ В РЕГРЕС- ! ЗНАЧ.ПАРАМЕТРА !    ЗНАЧ.   !
     !    СИОННОЕ УРАВНЕНИЕ         !   РЕГРЕССИИ    ! T-КРИТЕРИЯ !
     !                              !                !            !
     !                 1            !   .6798300E+00 !     7.055  !
     !                 2            !   .7341768E+00 !     7.666  !
     !                 3            !   .4851218E+00 !     4.706  !
     !                 4            !   .4797908E+00 !     4.744  !
 
  ОСТАТОЧНАЯ ДИСПЕРСИЯ=  .534917E-01
 
  ОСТАТОЧНАЯ СУММА КВАДРАТОВ=  .90936E+00
 
  ОТНОШЕНИЕ ДИСПЕРСИЙ F=    .15890
 
  КОЭФФИЦИЕНТ МНОЖЕСТВЕННОЙ КОРРЕЛЯЦИИ =  .930
 
  GAMMA=      2.51
 
  КОЭФФИЦИЕНТЫ МОДЕЛИ В НАТУРАЛЬНОМ МАСШТАБЕ
 
 B( 1)=  .402263E+00  B( 2)=  .459078E+00  B( 3)=  .268561E+00  B( 4)=  .368791E+00
B( 5)= -.714040E-01
 
 
 ----------------------------------------------------------
 ----------------------------------------------------------
 
  ДИСПЕРСИОННАЯ МАТРИЦА ПЛАНА
 
 
    .608E-01
 
    .218E-01    .670E-01
 
    .120E-01    .822E-02    .609E-01
 
   -.582E-03   -.647E-02    .373E-01    .113E+00
Скачать файл