Методичні вказівки до виконання практичних та лабораторних робіт з курсу «Обчислювальна техніка та програмування», страница 8

Може виявитися, що значення Cn буде обчислюватися більш просто, якщо скористуватися рекурентним співвідношенням

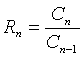                                    (3)

Тоді

                                   (4)

Пояснимо на прикладі. Нехай необхідно просумувати ряд

ⁿ                              (5)

З точністю e=1E-4 в крапці X₀=0. 5.

При обчисленні Сn безпосередньо з формули (2) виникає необхідність при кожному n обчислювати міри X_2n-1 і факторіали (2n+1)!. При більших n ця процедура знижує як швидкість, так і точність обчислень.

Обчислення же C_n за допомогою рекурентного співвідношення виявляється більш простими. Справді, якщо підставити в (3) значення C_n і C_n-1 і, виконавши необхідні перетворення, отримаємо

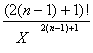
R= (6)

Підставивши отримане значення R у (4), маємо рекурентну формулу для обчислення Cn:

                                     (7)

В цьому випадку алгоритм обчислень можна організувати наступним образом:

n=0; x=0. 5; e=1e-4;

Перед входом в ітераційний цикл у s1 заноситься значення x. Тому

s1=x; s=s1;

Доки |x|> повторювати

s1*=x*x/(2*n* (2*n+1));

s=s1.

Нижче приводиться приклад програми виконаної на мові C++.

#include <stdio.h>

#include <iostream.h>

#include <math.h>

void main ()

{int n=1, k;

float x=0.5, e=1.0E-10, s, s1;

s=s1=x;

while (s1>e)

{s1*=x*x/(2*n* (2*n+1));

cout<<"s1="<<s1<<'\n';

s+=s1; n++;}

cout<<"s="<<s<<'\n';

cin>>n;

}

1.3 Варіанти індивідуальних завдань лабораторної роботи №1

	Обчислити суму ряду	З точністю
1	S=	=10-2
2	S=	=
3	S=	=
4	S=	=
5	S=n	=
6	S= (-1) n	=	X0=0. 3.
7	S= (-1) n	=	X0=/9.
8	S= (-1) n+1	=	X0=1. 6
9	S= (-1) n+1	=	X0=1. 22
10	S= (-1) n	=	X0=0. 6785
11	S=	=
12	S= (-1) n+1	=
13	S=n	=
14		=
15	S=	=
16	S= (-1) n	=	X0=2. 44
17	S=	=
18	S=4 (-1) n	=10-2
19	S=	=	X0=2. 334
20	S=	=
21	S=2	=	X0=0. 4357
22	S=	=10-2
23	S=	=
24	S=	=
25	S=	=
26	S=	=
27	S=	=
28	S=	=10-2
29	S=4(-1)n+1	=10-2
30	S=(n-1)	=10-5