Исследование цепей второго порядка, страница 8

;

Подставим:, , , ,  , ;

Получаем:

;

Подставим численные значения:

;

Находим корни характеристического уравнения: ;  ;

Представим выражение в виде:

;

Чтобы найти оригинал по Лапласу от этого выражения, воспользуемся теорией вычетов:

.

.

;

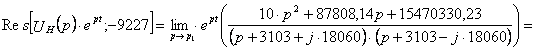
Сумма вычетов комплексно сопряженной части равна удвоенной реальной части:

;

Находим оригинал суммированием вычетов:

.

Полученное выражение описывает переходный процесс в заданной цепи.

3.2 Построение и расчет графика переходного процесса в цепи.

Воспользуемся выражением, описывающим переходный процесс в данной схеме:

.

Найдем несколько значений  и занесем их в таблицу 3.1.

Таблица 3.1 – Значения

t, сек	0.00001	0.00017	0.00025	0.00035	0.0005	0.00068	0.00075
, В	9.99	-6.8	-0.17	3.83	-2.21	1.31	0.54
t, сек	0.00083	0.001	0.00104	0.00122	0.00125	0.00139	0.0015
, В	-0.77	0.36	0.45	-0.27	-0.18	0.09	0.05