Исследование цепей второго порядка, страница 3

;                                                   (1.7)

 c^-1

;                                                (1.8)

 Oм

;                                            (1.9)

 Ом

Как было сказано выше, сопротивление нагрузки зависит только от сопротивления холостого хода и сопротивления короткого замыкания относительно клемм 2-2’.

Определим . Для этого приведем исходную схему к виду, представленному на рисунке 1.3

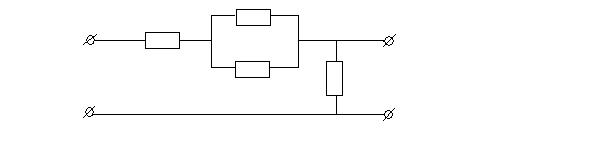
                                Рис. 1.3   Схема для расчета Z_2X 

Z_2X будет равно: 

 Ом

При нахождении сопротивления короткого замыкания  на клеммы 1-1’ необходимо поставить перемычку (рис. 1.4)

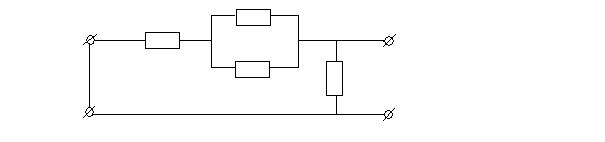
                                Рис. 1.4  Схема для расчета Z_2K

Из рисунка 1.4 видно:

 -резистор и конденсатор соединены параллельно, поэтому:

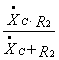=;                                              (1.10)

-резистор  и  соединены последовательно, а значит:

= +;                                             (1.11)

-индуктивность и  соединены параллельно и мы получаем выражение:

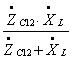=;                                            (1.12)

Подставив формулы 1.10 и 1.11 в 1.12 окончательно получаем:   

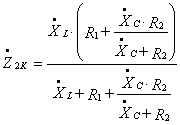;                           (1.13)  

Подставим в формулу 1.13 численные данные:

 Ом ;

Подставим полученные значения и в формулу 1.6

 Oм

Стало быть, сопротивление нагрузки есть ничто иное, как последовательно соединенные резистор  и катушка индуктивности  (рис 1.5).

 Ом

 Ом

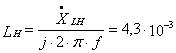 Гн

Рис 1.5 Представление нагрузки в виде пассивной и реактивной частей

Таким образом,  если взять сопротивление нагрузки, равное , то в нагрузку будет передаваться максимум мощности.

1.2  Расчет цепи с найденным сопротивлением нагрузки

Рассчитаем схему (рис1.6) с найденными значениями нагрузки методом эквивалентного преобразования. Для этого представим схему в комплексной форме (рис 1.7)