Обработка результатов двух групп многократных измерений, страница 9

Необходимо определить вид степенного полинома, описывающего функциональную связь между описываемыми величинами. Сначала предположим, что начальным полиномом является линейная зависимость .

Составим систему нормальных уравнений для  группы измерений, решив которую найдем искомые неизвестные А и В.

Нормальные уравнения будут такими:

Решаем нормальные уравнения методом определителей:

 

 

 

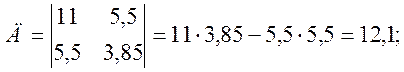
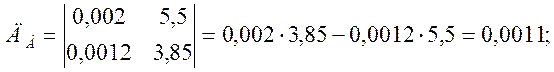
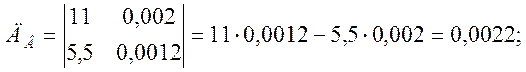
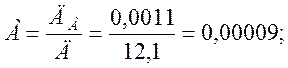
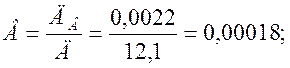
Определим параметры аппроксимирующей линейной зависимости

Расчётную абсолютную погрешность рабочего вольтметра аппроксимируем следующей линейной зависимостью:

Оценку дисперсии   условных уравнений определяем из соотношения:

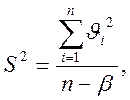
где - невязка в i-й точке диапазона;

- число точек диапазона;

- число искомых неизвестных;

В нашем случае:

- расчётное значение погрешности в i-й точке диапазона;

- экспериментальное значение погрешности в i-й точке диапазона.

Оценку дисперсии   условных уравнений определяем из соотношения:

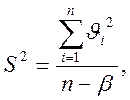
где - невязка в i-й точке диапазона;

- число точек диапазона;

- число искомых неизвестных;

- расчётное значение погрешности в i-й точке диапазона;

- экспериментальное значение погрешности в i-й точке диапазона.

Таблица 10.5 – Расчётное значение погрешности в i-й точке диапазона 1-ой группы измерений

0,002	0,00205	0,0021	0,00215	0,0022	0,00225	0,0023	0,00235	0,0024	0,00245	0,0025

Находим отклонения:

Таблица 10.7 – Отклонения группы измерений

0,53150	0,62765	-0,0432	-0,56005	-0,5669	-0,45325	-0,2946	-0,10745	0,0852	0,29085	0,4885

Таблица 10.9 – Значения входных напряжений, абсолютных и теоретических погрешностей и их отклонений  группы измерений

	0	0,1	0,2	0,3	0,4
	-0,5295	-0,6256	0,0453	0,5622	0,5691
	0,002	0,00205	0,0021	0,00215	0,0022
	0,53150	0,62765	-0,0432	-0,56005	-0,5669

0,5	0,6	0,7	0,8	0,9	1,0
0,4555	0,2969	0,1098	-0,0828	-0,2884	-0,4860
0,00225	0,0023	0,00235	0,0024	0,00245	0,0025
-0,45325	-0,2946	-0,10745	0,0852	0,29085	0,4885

Оценки дисперсии и СКО:

Оценки дисперсии значений коэффициентов А и В  получаем из соотношений:

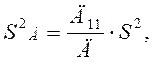
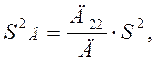
где - условных уравнений;

- алгебраические дополнения элементов  и , получаемые путём удаления из матрицы определителя  столбца и строки, на пересечении которых находится данный элемент.

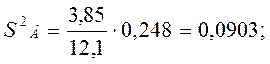
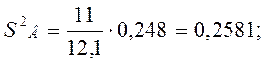
             Средние квадратические отклонения характеризуют вероятную погрешность полученных значений А и В и могут быть использованы для вычисления доверительных интервалов оценок А и В. Т. к. данное распределение не подчиняется нормальному закону распределения, формула для определения доверительных интервалов будет иметь вид

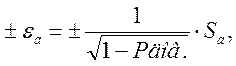
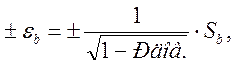
где

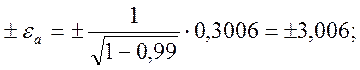
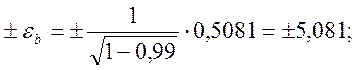
 при   

 при

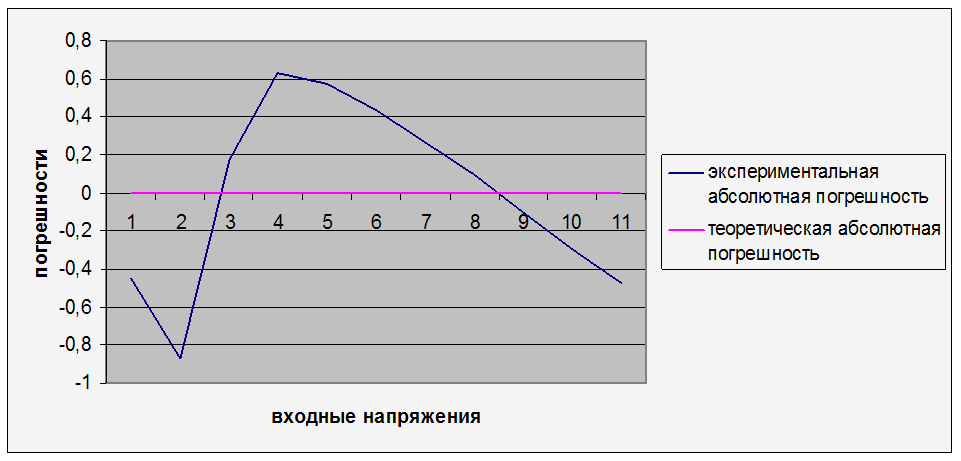
Рис. 10.4 –Абсолютные погрешности 2-ой группы измерений

10.3 Определяем класс точности и относительную погрешность измерительного преобразователя.

Относительную погрешность вольтметра оценим следующей зависимостью:

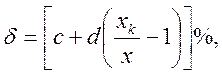
где

- конечное значение измеряемой величины для выбранного диапазона.

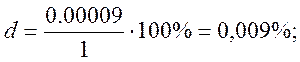
Из стандартного ряда:

Тогда получаем:

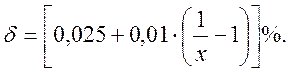
Вывод

          В ходе данной научной работы были обработаны результаты полученных измерений. Данные результаты измерений были получены на одном и том же приборе, который работал в двух режимах (показания снимались непосредственно сразу после включения прибора и после тридцатиминутного перерыва между измерениями). Вследствие неточности изготовления самого прибора, присутствия погрешности гистерезиса, показания двух таблиц несколько различались. Сначала мы находили все оценки для дальнейшей обработки результатов, затем, с целью получения из двух таблиц одной, мы проверяли по Т-критерию результаты измерений (данные рез-ты измерений  оказались неоднородными); исследовали на неравноточность по критерию Фишера. Т.к. результаты первоначально измерялись при задавании контрольных точек, то для того, чтобы увидеть экспериментальную гистограмму распределения напряжений, мы вынуждены были находить значения отклонений каждого из результатов измерения напряжения в данной контрольной точке от среднего арифметического значения в этой же точке. Таким образом, мы получили экспериментальную гистограмму отклонений значений от САЗ, которая, для проверки нормальности закона распределения , сравнивалась с теоретической гистограммой. В нашем случае нормальность закона распределения не подтвердилась, и  мы высунули еще одну гипотезу по поводу закона распределения, которая тоже не дала положительный результат. Затем мы находили теоретическую СХП, теоретическую погрешность и сравнивали их с экспериментальными значениями. В конечном счете мы получили относительную погрешность вольтметра.

Список использованной литературы:

1. Абрамов Л. А., Науменко А. М. Изучение цифровых омметров и оценка точности изготовления резисторов на основании обработки результатов равноточных измерений: Описание лабораторной работы.- Харьков «ХАИ», 1991.

2. Науменко А. М., Чебыкина Т. В. Методы обработки результатов экспериментов: Методические рекомендации по выполнению лабораторных работ.- Харьков «ХАИ», 2003.