Обработка результатов двух групп многократных измерений, страница 4

 Таблица 6.4 –Абсолютная погрешности гистерезиса для второй таблицы

-0,004	-0,024	0,06	0,002	0	0,002	0,01	0,01	0,004	-0,004	0

6.3 Вычисляем значения относительной

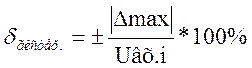
и приведенной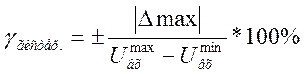                         

погрешностей гистерезиса результатов измерения.

Для 1-ой группы: + (0,142/0,2)*100% = + 71%

                               + (0,142/1,0)*100% = +14,2%

Для 2-ой группы: + (0,06/0,2)*100% = +30%

                               + (0,06/1,0)*100% = + 6%

Т. е. γ1,2 =       →  γкл.=

6.4 Построим графики погрешностей, связанных с гистерезисом для двух таблиц.

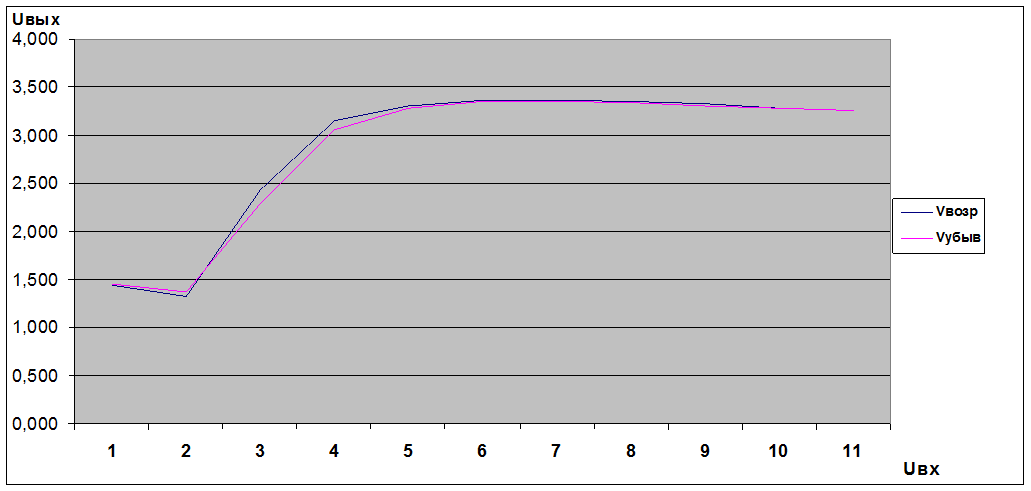
Рис 6.5 – Погрешность гистерезиса для первой таблицы

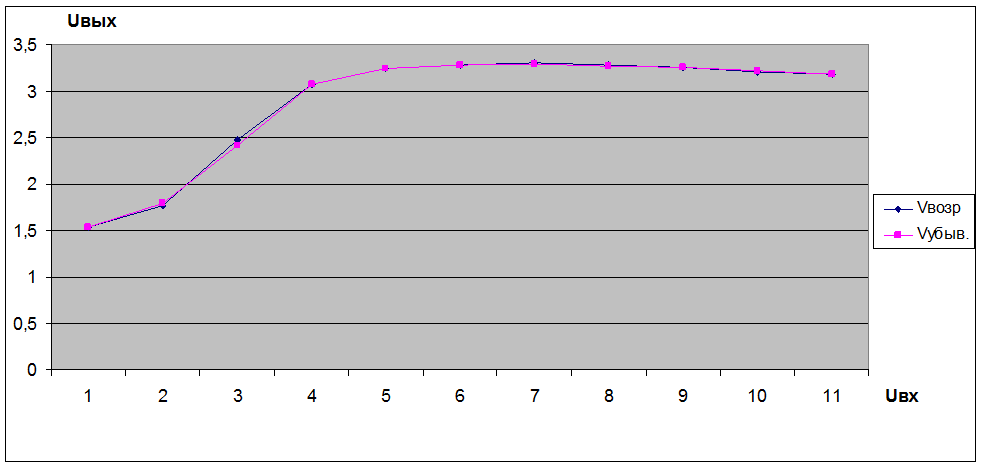
                 Рис 6.6 – Погрешность гистерезиса для второй таблицы

Для двух таблиц погрешность гистерезиса является несущественной.

7. Проверка на однородность по Т-критерию

          7.1 Определяем вид погрешности (аддитивная или мультипликативная) по графику СХП.

По построенной статической характеристике преобразования видно, что в данных измерениях присутствует лишь аддитивная составляющая погрешности.

          7.2 Выполняем проверку результатов измерения на однородность по данному критерию.

Проверим, какой характер расхождения средних значений рядов измерения выходного напряжения- систематический или случайный. Чтобы выявить, содержат ли средние значения систематические составляющие погрешности измерения напряжения, проводят проверку по Т-критерию. Если разность наибольшего  и наименьшего  средних значений оказывается больше допустимого, то результаты рядов измерений являются неоднородными и объединяться не могут без устранения систематической погрешности.

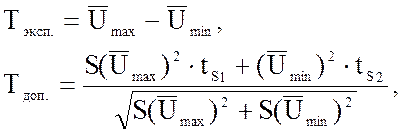
где  и  - коэффициент Стьюдента, которые выбирают из таблицы статистики Стьюдента в зависимости от значения доверительной вероятности  и числа степеней свободы  и .

При  максимальное расхождение средних значений признают случайным, систематическую составляющую погрешности - несущественной и результаты измерений, полученные для одной отметки шкалы , можно объединить.

 - число степеней свободы

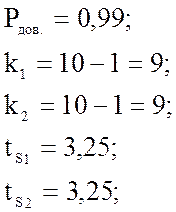
Таблица 7.1 – Экспериментальные и допустимые значения Т- критерия

		0,087	0,434	0,075	0,034	0,051	0,067	0,063	0,062	0,064	0,070	0,068
	0,108		0,381	0,671	0,277	0,116	0,077	0,070	0,059	0,063	0,069	0,056

Для контрольных точек  0.1, 0.7, 0.8, 0.9 и 1.0 результаты измерения напряжений являются неоднородными, а для остальных – однородными.

Вводим поправку с= -0,011 в одну из групп измерений, прибавляя поправку (с) к средним значениям результатов измерения 1-ой группы (к первому графику, который расположен ниже второго).

 Таблица 7.2 – Средние значения рез-тов измерения после введения поправки

1,436	1,335	2,354	3,094	3,278	3,341	3,349	3,330	3,307	3,273	3,243

А теперь снова производим проверку на однородность результатов измерения.

Таблица 7.3 – Экспериментальные и допустимые значения Т- критерия после введения поправки

	0,098	0,445	0,086	0,023	0,040	0,056	0,052	0,051	0,053	0,059	0,057
	0,1075	0,3812	0,6712	0,2774	0,1156	0,0767	0,0669	0,0591	0,0632	0,0692	0,0561

          Неоднородными являются значения результатов измерения только в 0,1 и 1,0 контрольных точках. Поправка дала положительный результат, как видно, расхождения небольшие, следовательно, результаты измерений двух групп можна считать однородными.

         7.3 Проверим результаты измерений напряжений Uвых 1-й группы и Uвых 2-й группы на равнорассеяность. Равнорассеяность определяют по критерию Фишера, полученное значение Fэксп сравнивают с Fдоп ( Fдоп=5.35 для Рдов=0.99 k1=k2=9).

Если неравенство выполняется, то дисперсии признают равнорассеяными, а результаты измерений  -  равноточными.

Таблица 7.4 – Экспериментальные и допустимые значения F- критерия. 

Fэксп	5,840	3,423	3,909	1,365	3,126	4,894	1,366	1,310	2,269	1,488	1,161
Fдоп	5,35	5,35	5,35	5,35	5,35	5,35	5,35	5,35	5,35	5,35	5,35

Как видим, в точке 0,0 результаты измерений оказались не равноточными, а во всех остальных – равноточными, следовательно, результаты измерений будем считать равноточными.

          7.4 Проверим результаты измерений напряжений Uвых 1-й группы и Uвых 2-й группы на наличие корреляционной связи.

           Наличие корреляционной связи оценивают, вычисляя коэффициент корреляции, и сравнивают с допустимым значением(Rдоп=0,735 для Рдов=0.99).

Таблица 7.5 – Экспериментальные и допустимые значения R- критерия

Rэксп	0,2069	-          0,3524	-0,3337	-0,1971	-0,4414	-0,6455	-0,7303	-0,7949	-0,6617	-0,6247	-0,8680
Rдоп	0,735	0,735	0,735	0,735	0,735	0,735	0,735	0,735	0,735	0,735	0,735

             7.5 Определим оценку существенности корреляционной связи:

(ts – коэффициент Стъюдента , который выбирают по статистике распределения Стъюдента в зависимости от Рдов и k).

            Если неравенство выполняется, то корреляционная связь признается несущественной и можно не учитывать ее в дальнейших вычислениях, а сами результаты измерений считать независимыми.