Обработка результатов двух групп многократных измерений, страница 3

          3.2 Вычисляем оценку среднего квадратического отклонения (СКО) результатов наблюдений    

                                                         ,

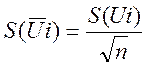но сначала находим дисперсию

 

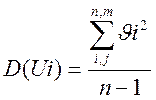
и СКО результатов измерений

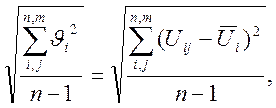
Таблица 3.3 – Дисперсия, СКО  и оценка СКО для первой таблицы

D(Ui)	0,000934	0,010648	0,033961	0,006364	0,000959	0,000462	0,000240	0,000187	0,000262	0,000182	0,000137
S(Ui)	0,030570	0,103190	0,184290	0,079770	0,030960	0,021500	0,015630	0,013700	0,016190	0,013500	0,011740
	0,009667	0,032632	0,058278	0,025225	0,009790	0,006800	0,004943	0,004332	0,005119	0,004270	0,003713

Таблица 3.4 – Дисперсия, СКО и оценка СКО для второй таблицы

D(Ui)	0,000160	0,003100	0,008680	0,000921	0,000306	0,000094	0,000178	0,000143	0,000115	0,000271	0,000160
S(Ui)	0,012649	0,055777	0,093214	0,030350	0,017512	0,009718	0,013375	0,011972	0,010750	0,016465	0,012649
	0,004000	0,0176382	0,0294768	0,0095975	0,0055378	0,0030731	0,0042295	0,0037859	0,0033995	0,0052067	0,00400

4. Проверка на наличие промахов по критерию Смирнова, трех сигм

4.1 Критерий «трёх сигм»

Если , то грубой ошибки нет, а если , то есть грубая ошибка.

Таблица 4.1 – Проверка на наличие грубых ошибок для первой таблицы

	0,053	0,176	0,325	0,175	0,051	0,038	0,030	0,031	0,038	0,026	0,016
	0,09171	0,30958	0,55286	0,23932	0,09289	0,06450	0,04690	0,04111	0,04858	0,04050	0,03521

Таблица 4.2 – Проверка на наличие грубых ошибок для второй таблицы

	0,016	0,080	0,160	0,031	0,038	0,015	0,023	0,021	0,016	0,026	0,024
	0,037947	0,167332	0,279643	0,091049	0,052536	0,029155	0,040125	0,035917	0,032249	0,049396	0,037947

По критерию «трёх сигм» грубая ошибка не обнаружена ни в одном из проведенных опытов.

4.2 Критерий Смирнова ( tсмирн.=2.41 при Pдов.=0,99)

Если 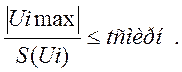, то промахов нет, а если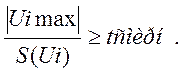, то промахи есть.

Таблица 4.3 – Проверка на наличие промахов для первой таблицы

tcмирн.	2,41	2,41	2,41	2,41	2,41	2,41	2,41	2,41	2,41	2,41	2,41
	1,73380	1,70553	1,76357	2,19370	1,64707	1,76749	1,91881	2,26224	2,34665	1,92607	1,36311

Таблица 4.4 – Проверка на наличие  промахов для второй таблицы

tcмирн.	2,41	2,41	2,41	2,41	2,41	2,41	2,41	2,41	2,41	2,41	2,41
	1,26	1,43	1,72	1,95	2,17	1,54	1,72	1,75	1,49	1,58	1,90

По критерию Смирнова промахов не обнаружено ни в одном из проведенных опытов.

5. Построение экспериментальной статической характеристики преобразования (СХП)

Строим статическую характеристику преобразования (СХП) для первой и второй таблиц на одном графике.

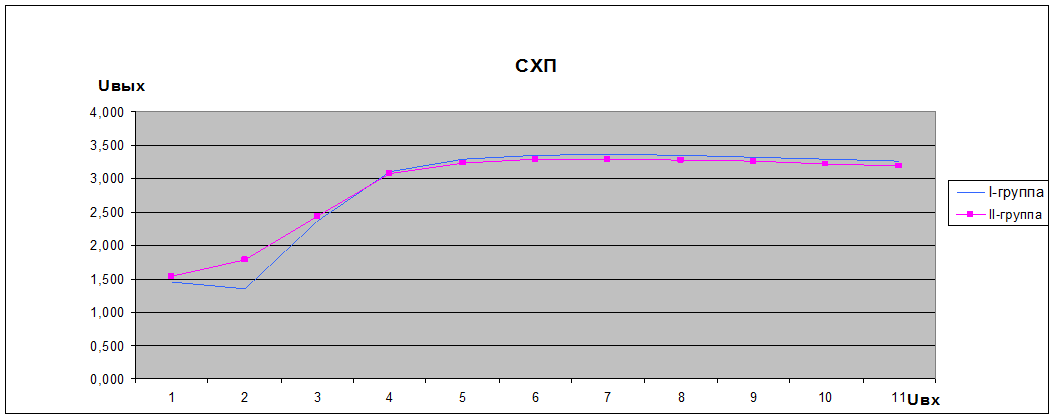
Рис.5.1- Статическая характеристика преобразования для 2-х таблиц

6. Оценивание значений абсолютной и относительной погрешностей выходного сигнала от гистерезиса

6.1 Вычисляем средние значения результатов наблюдений в каждой точке диапазона при возрастании и убывании измеряемого напряжения.

 

        

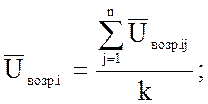
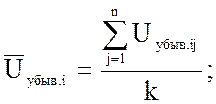
Таблица 6.1 – Напряжения возрастания и убывания для первой таблицы

1,444	1,324	2,436	3,152	3,300	3,358	3,366	3,346	3,328	3,284	3,256

1,450	1,368	2,294	3,058	3,278	3,346	3,354	3,336	3,308	3,284	3,252

Таблица 6.2 – Напряжения возрастания и убывания для второй таблицы

1,532	1,768	2,470	3,072	3,238	3,286	3,302	3,284	3,256	3,212	3,186

1,536	1,792	2,410	3,070	3,238	3,284	3,292	3,274	3,252	3,216	3,186

6.2 Определяем абсолютную погрешность гистерезиса, вычисляя средние значения результатов наблюдений в каждой точке диапазона при возрастании и убывании измеряемого напряжения.

Таблица 6.3 – Абсолютная погрешности гистерезиса для первой таблицы

-0,006	-0,044	0,142	0,094	0,022	0,012	0,012	0,010	0,020	0,000	0,004