Обработка результатов двух групп многократных измерений, страница 7

Таблица 8.5 – Экспериментальные частоты каждого интервала.

n1	n2	n3	n4	n5	n6	n7	n8	n9
2	3	6	3	85	96	11	8	6

       8.4 Находим среднее значение каждого интервала

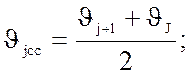
Таблица 8.6 – Средние значения каждого интервала измерений

υ1ср	υ2ср	υ3ср	υ4ср	υ5ср	υ6ср	υ7ср	υ8ср	υ9ср
-0,3552	-0,2796	-0,204	-0,1284	-0,0528	0,0228	0,0984	0,174	0,2497

          8.5 Подсчитываем плотности распределения вероятности для каждого интервала

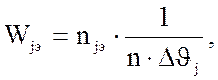
где n и - постоянные величины для измеряемой выборки.

Шаг для каждого интервала группы измерений –= 0,0756.

Таблица 8.7 – Плотности распределения вероятности для каждого интервала 1-ой группы

0,12	0,18	0,36	0,18	5,1	5,76	0,66	0,48	0,36

          8.6 Построим гистограммы экспериментального распределения.

          Построим гистограмму распределения в виде прямоугольников, откладывая по оси абсцисс интервалы  в порядке возрастания их номеров, а по оси ординат - экспериментальные частоты , пропорциональные плотности распределения вероятностей.

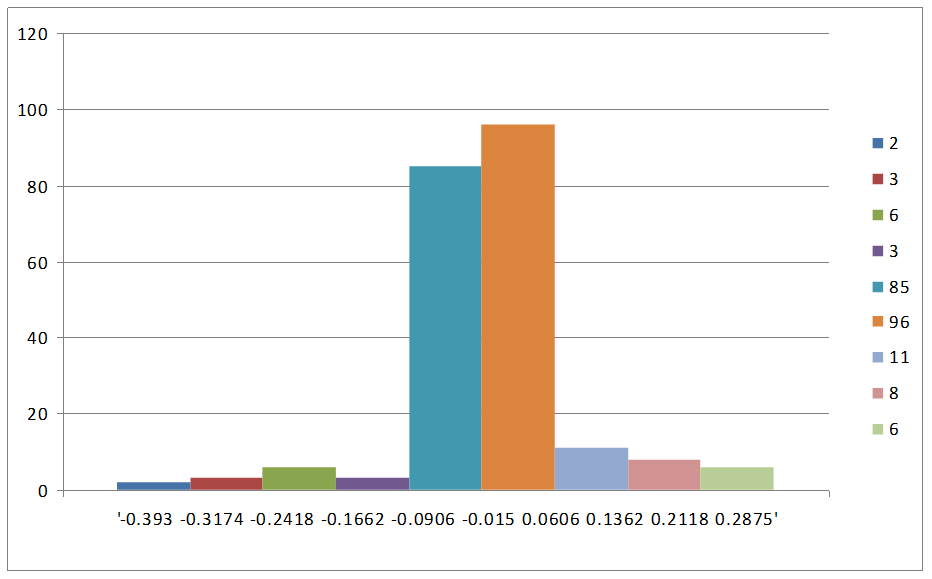
Рис 8.1 – Экспериментальная гистограмма распределения отклонений напряжений

          8.7 Построим теоретическую гистограмму распределения.

          Проверку на нормальность экспериментального распределения при большом числе результатов измерений проведём путём построения теоретической гистограммы и оценивания её соответствия экспериментальной гистограмме.

          Вычислим нормированные отклонения середины каждого интервала гистограммы от САЗ напряжений .

Находим значение САЗ отклонений  по формуле:

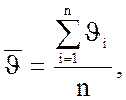
v=0/220=0.

Находим значение СКО

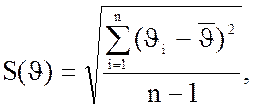
 =0,09

Нормированные отклонения середины каждого интервала гистограммы от САЗ напряжений:

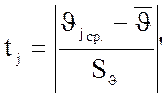
Таблица 8.9 - Нормированные отклонения середины каждого интервала гистограммы от САЗ напряжений 1-ой группы

3,95	3,11	2,27	1,43	0,59	0,25	1,09	1,93	2,77

          Определим по таблице нормированной функции нормального распределения плотность вероятности   для каждого интервала гистограммы:

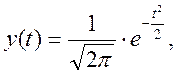
Таблица 8.10 - Плотность вероятности  для каждого интервала гистограммы.

y(3,95)	y(3,11)	y(2,27)	y(1,43)	y(0,59)	y(0,25)	y(1,09)	y(1,93)	y(2,77)
0,0002	0,0032	0,0303	0,1435	0,3352	0,3867	0,2203	0,062	0,0086

          Вычисляем теоретические частоты  (теоретическое число результатов измерения), соответствующие каждому интервалу:

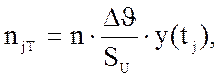
Таблица 8.11 - Теоретическое число результатов измерения.

0,4	0,6	5,5	26,5	62	71,5	40,5	11,5	1,5

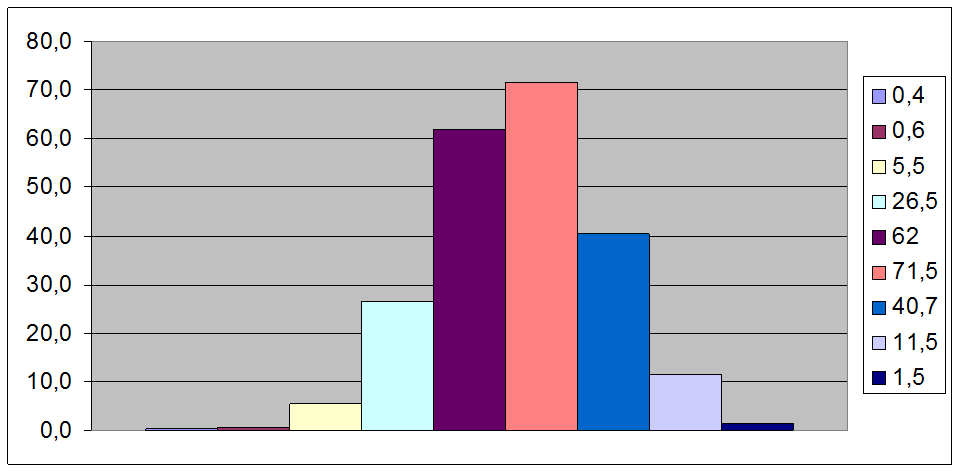
Рис 8.3 – Теоретическая гистограмма распределения отклонений напряжений

          8.8 Проверяем соответствие экспериментальной гистограммы теоретической.

          При большом числе опытов проверка соответствия экспериментальной и теоретической гистограмм выполняется с использованием критерия согласия - Пирсона, обеспечивающего минимальную ошибку принятия гипотезы по сравнению с другими критериями.

          Показатель разности частот экспериментального и теоретического распределений можно вычислить по формуле

,

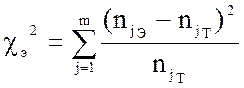где m- число интервалов гистограммы после их укрупнения.

Для 1-ой группы измерений:

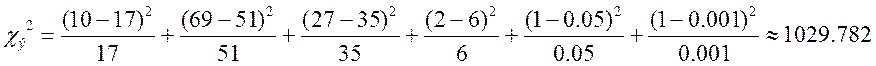  (90 – мое )

          Критерий  зависит от числа степеней свободы k и выбираемого уровня значимости q. Число степеней свободы , где d- число независимых условий (ограничений), принятых при определении значений плотности вероятности. Для нормального распределения существуют три таких условия(d=3):

          Уровень значимости q должен быть достаточно малым, чтобы была малой вероятность отклонения правильной гипотезы. С другой стороны, чрезмерно малый уровень значимости увеличивает вероятность принятия ложной гипотезы. Из опыта практического применения критерия следует ограничить выбор q-интервалом .

          По уровню значимости q и числу степеней свободы k=r-3, по таблице  - распределения находят границу критической области критерия . Если оказывается, что ,то гипотеза о нормальности отвергается, если то экспериментальное распределение относят к нормальному.

          Вместо односторонней критической области  часто применяют двусторонние критические области и , соответствующие и .

          Для нахождения и уровень значимости делится на две части обычно (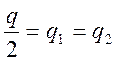). По таблице критерия для выбранного уровня значимости и числа степеней свободы k=r-3 определяют  для  и  для .

          Гипотеза о нормальности проверяемого распределения принимается, если .

Для 1-ой группы измерений:

1) к =m-3,где m-число интервалов гистограммы после их укрупнения, тогда:

k=9-3=6;

интервал:;

пусть

при k=3 и q=0,02 имеем   (15,033 и 16,812)

2) k=6-3=3;

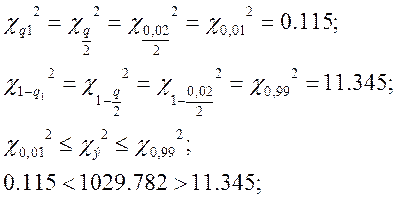
Следовательно, данное распределение является ненормальным.

          Предположим, что данные распределения подчиняются експонециальному закону распределения, а именно двойному  експонециальному закону распределения (Лапласа), который имеет вид:

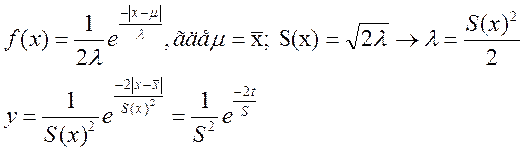
Для 1-ой группы измерений:

(

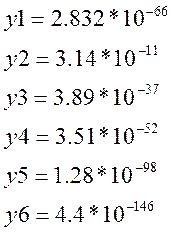          По расчетным значениям нормированных функций двойного экспоненциального распределения (Лапласа)   видно, что данное распределение не является экспоненциальным. Следовательно, нам не нужно проверять соответствие экспериментальной гистограммы теоретической  по критерию согласия - Пирсона для данного закона распределения.