Проектирование железобетонного моста средней длины предназначенного для пропуска однопутной железной дороги колеи 1520мм через водоток, страница 6

Исходя из всего выше сказанного целесообразно сооружение второго варианта, поэтому для дальнейших расчетов примем именно этот вариант.

4    Статический расчет пролетного строения.

Железобетонные пролетные строения представляют собой сложные пространственные конструкции, рассчитываемые в проектных организациях, как правило, на ЭВМ.

В курсовом проекте разрешается применять приближенные расчетные схемы, по которым пролетное строение условно расчленяется на плиту проезжей части и главные балки, рассчитываемые отдельно, но с частичным учетом их совместной работы.

4.1. Расчет плиты балластного корыта.

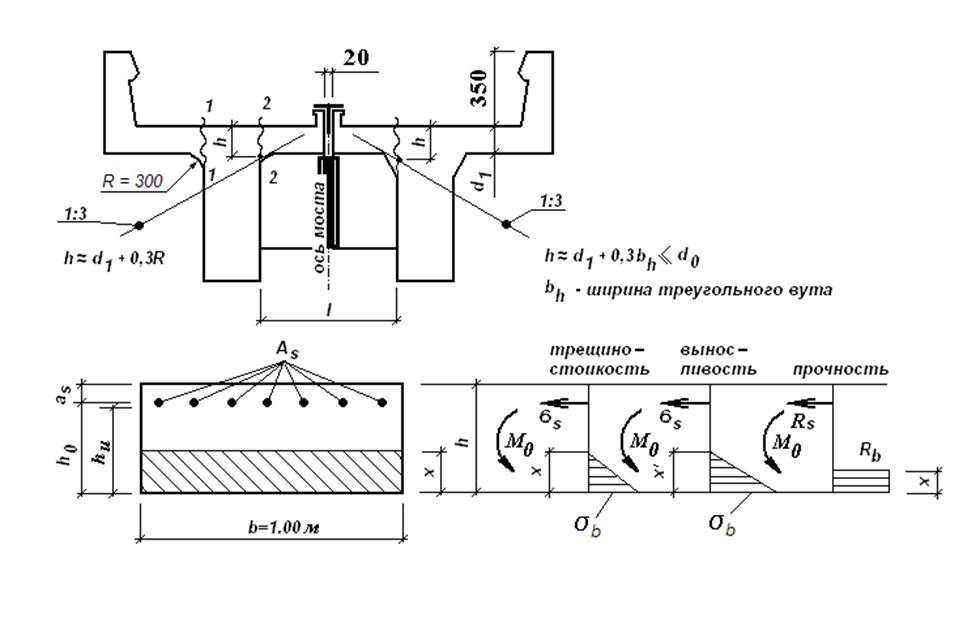
Рисунок 1 -Схемы к расчету плиты балластного корыта.

Исходные данные для расчета:

– L = 23,6м – полная длина пролета;

– В 45 – класс бетона;

– А II – класс арматуры;

– = 0,2м – толщина плиты;

– В = 1,8м - расстояние между осями балок;

– В₁ = 4,18м – ширина балластного корыта.

4.1.1    Нормативные постоянные и временные нагрузки.    

На внешнюю консоль действуют нагрузки, которые можно определить по следующим формулам:

Нагрузка от собственного веса плиты балластного корыта:

                                                    ,                                                      (4.1)

где =24,5 кН/м - удельный вес железобетона, d₁ = 0,2м – толщина плиты.

Нагрузка от веса мостового полотна:

                                                    ,                                                    (4.2)

где =19,6кН/м - удельный вес балласта с частями пути, d₂ = 0,35м – толщина балласта под шпалой.

Нагрузка от тротуаров: .

Нагрузка от перил: .

Нагрузка от подвижного состава, передаваемая на внешнюю консоль:

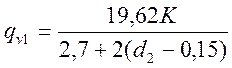                                             ,                                          (4.3)

где К =13 - класс нагрузки (по заданию).

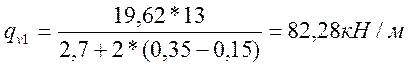
Нагрузка от подвижного состава, передаваемая на правую консоль: 

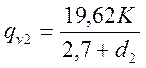                                                     ,                                            (4.4)

где К = 13 - класс нагрузки (по заданию).

.

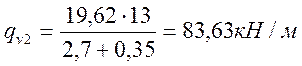Данные нагрузки на расчетной схеме распределяются по следующим длинам:

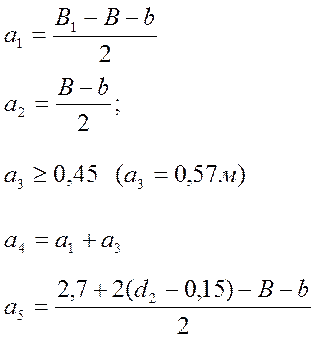                                           ,                                (4.5)

где b = 0,28м – толщина стенки; B₁ = 4,18м - ширина балластного корыта.

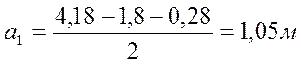
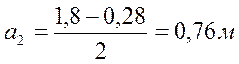
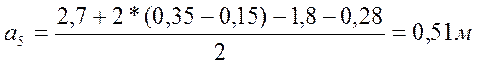
4.1.2    Расчетные усилия.

За расчетные сечения принимаем те сечения плиты, где действуют максимальные изгибающие моменты M₁ (на внешней консоли) и М₂ (на внутренней) (рисунок 1).

Расчет плиты производится по предельным состояниям первой группы (на прочность и выносливость) и второй группы (на трещиностойкость).

	Рисунок 2 - Расчетные эпюры напряжений в плите балластного корыта.

Таким образом, значения моментов определяются:

1)  для расчета на прочность:

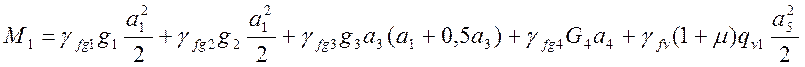   ;  (4.6)

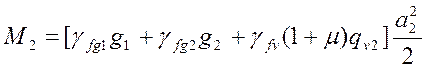                                ,                           (4.7)

                  ;            (4.8)

                                 ;                            (4.9)

2)  для расчета на выносливость:

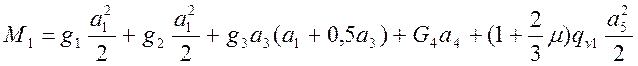                  ;         (4.10)

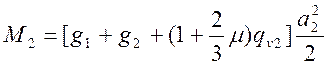                                        ;                               (4.11)

3)  для расчета на трещиностойкость:

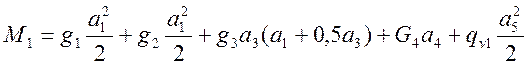                          ;                 (4.12)

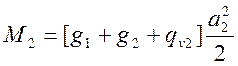                                               ;                                  (4.13)

где - коэффициенты надежности по постоянным нагрузкам, взятые в соответствии с п.2.10 /1/ равными:

- коэффициент надежности по постоянным нагрузкам по п.2.32/1/;

- коэффициент надежности по весу балласта по п.2.32 /1/;

 - коэффициент надежности по временной нагрузке по п.2.32 /1/;

(1+μ) – динамический коэффициент, равный 1,5 по п.2.22/1/.

Для расчетов на прочность:

.

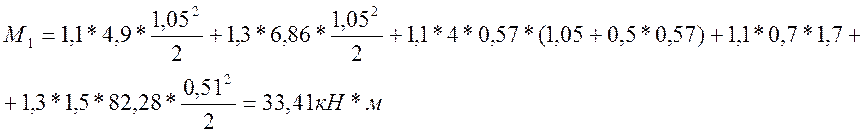
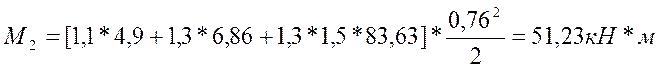
Для расчетов на выносливость:

.

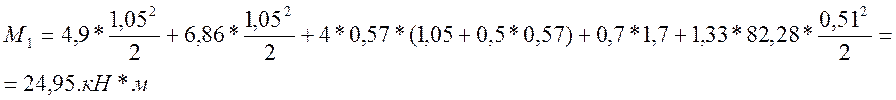
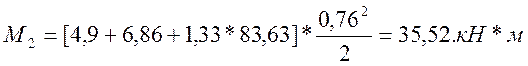Для расчетов на трещиностойкость

.

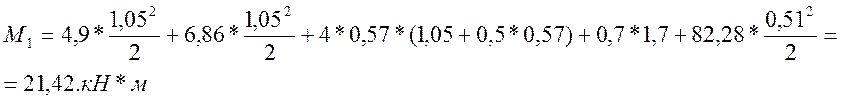
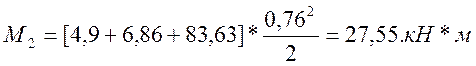В дальнейшем расчеты производим на наибольшие значения изгибающих моментов и поперечных сил. Наибольшие значения получаются на внутренней консоли, поэтому далее рассчитываем внутреннюю консоль.

Расчетные значения изгибающих моментов

– на прочность M₀ = 51,23кН*м;

– на выносливость M₀ = 35,52кН*м;

– на трещиностойкость М₀ = 27,55кН*м.

Расчетное значение поперечной силы Q₀ = 134,81кН.

4.1.3    Определение расчетного сечения плиты и назначение площади арматуры.

Исходя из выше полученных результатов, в данном курсовом проекте будем осуществлять проверку сечения 1-1 консольной плиты (рисунок 2).

                                                 ,                                               (4.14)

где R = 0,3м – радиус вута, d₁ = 0,2м – толщина плиты.

Диаметр рабочей арматуры принимаем равным 12мм по п.3.118 /1/ Расстояние от центра тяжести площади сечения арматуры до растянутой грани плиты определяем по формуле:

                                             ,                                              (4.15)

где d = 0,012м – диаметр арматуры.

Тогда рабочая высота сечения плиты равна

Требуемая площадь арматуры определяется по формуле:

                                                 ,                                            (4.16)

где M₀ = 51,23кН*м – изгибающий момент для расчета по прочности; z =h₀*7/8 – плечо внутренней пары, м;  – расчетное сопротивление арматуры по п.3.37/1/, .

Плечо внутренней пары сил равно:

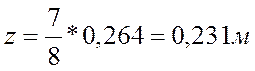
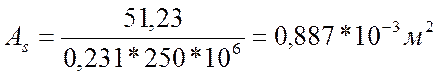
Количество стержней на 1п.м. ширины плиты определим по формуле:

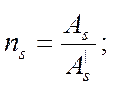                                                                                                              (4.17)

где  =0,1131*10^{-3 м2} - площадь одного стержня арматуры, принимаемая по таблице 4.1 /метода/.

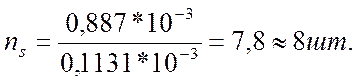
Уточняем площадь арматуры:

4.1.4    Расчет нормального сечения плиты по прочности.

Расчет производится на максимальное значение изгибающего момента из предположения, что напряжения в сжатой зоне бетона достигли величины расчетного сопротивления бетона на сжатие, и на растяжение бетон не работает. Расчет выполняется по прочности нормального сечения на действие изгибающего момента и на действие поперечной силы. Результатом расчета по прочности является проверка выполнения условий по расчетным формулам:

а) на прочность по изгибающему моменту: