Проектирование железобетонного моста под железную дорогу через водоток в Сибири, страница 9

Приведенный момент инерции сечения определен по формуле:

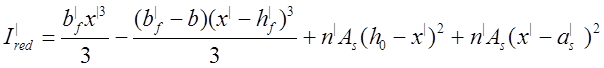,              (3.31)

Из формулы (3.31) определено:

.

Проверке удовлетворяет условие: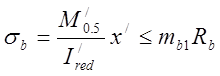

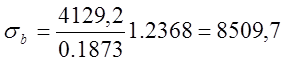 (кПа).

Расчетное сопротивления бетона на выносливость определено по формуле [3, п3.26]:

,                                             (3.32)

где ,  для  равны 1,26 и 1,163 соответственно.

Из формулы (3.32) определено:

кПа.

кПа.

Условие выносливости по бетону выполняется.

Напряжения в арматуре при расчете на выносливость определено по формуле:

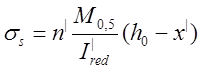,                                         (3.33)

Из формулы (3.33) определено:

МПа.

Расчетное сопротивление арматуры на выносливость рассчитано по формуле:

,                                             (3.34)

где ,  - величины постоянные, определяемые в соответствии [3 п.3.39], равные 0,882 и 1;  - расчетное сопротивление арматуры класса А-II, равное 250 МПа.

.

Условие выносливости по арматуре выполнено.

2) над опорой.

Используем те же формулы, что и в случае с расчётом в середине пролёта. Только подставляем соответствующие значения момента, площадей арматуры рабочей и сжатой.

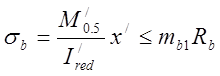, где , .

 

<.

.

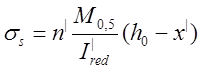Итак, окончательно после расчетов на выносливость принимаем расположение арматуры, как показано на рис.3.9.

3.8. Расчет балки по прочности наклонных сечений

Проверка прочности по сжатому бетону между наклонными трещинами производится по формуле [3, п.3.77]:

,                                      (3.35)

где =1686,8кН - поперечная сила на расстоянии не больше от оси опоры;  - определено по формуле , где =5 – при хомутах, нормальных к продольной оси элемента; =5,72 - отношение модулей упругости арматуры и бетона, определяемое по [3]; 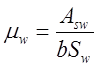, где =1,0053м - площадь сечения ветвей хомутов, расположенных в одной плоскости; =0,15м - расстояние между хомутами по нормали к ним; =0,324м - толщина ребра; =1,662м - рабочая высота сечения; .

1) над первой опорой.

        .

   2) над второй опорой.

=2,0106м; =0,15м; R_b=20МПа.

Назначается поперечное армирование на основании конструктивных требований.

Расчет наклонного сечения элемента с поперечной арматурой на действие поперечной силы производится из условия:

,                               (3.36)

где  - максимальное значение поперечной силы от внешней нагрузки;  и  - суммы проекций усилий всей пересекаемой арматуры по длине проекции сечения ;  - поперечное усилие, передаваемое в расчете на бетон сжатой зоны над концом наклонного сечения и определяемое по формуле:

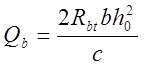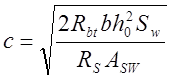,                                (3.37)

Расположение хомутов – как и в предыдущей проверке (3.35).

1)  над первой опорой.

, С=3,106.

2) над второй опорой.

, С=2,58.

.

В обоих случаях проверки наклонного сечения элемента с поперечной арматурой и прочности по сжатому бетону между наклонными трещинами выполняются.

3.9. Расчет балки на трещиностойкость.

Железобетонные балки с ненапрягаемой арматурой должны удовлетворять категории требований по трещиностойкости. Должно выполняться следующее условие:

 см,                                        (3.38)

где  - расчетная ширина трещины под нагрузкой

Ширину раскрытия наклонных трещин определяют по формуле:

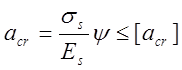,                                          (3.39)

где  - коэффициент раскрытия трещин, который учитывает влияние бетона растянутой зоны, деформации арматуры, ее профиль и условия работы элемента [3, п.3.105].

,

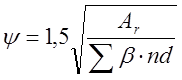где A_r=0,324*0,492=0,1594 м - площадь зоны взаимодействия для нормального сечения; =1 – коэффициент, учитывающий степень сцепления арматуры с бетоном; n – число арматурных элементов; d – диаметр одного стержня; R_r – радиус армирования.

Растягивающие напряжение  в поперечной и продольной арматуре стенок балок определены по формуле:

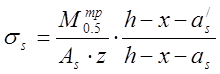,                                       (3.40)

1) проверка середины среднего пролёта.

A_s=0,01628 м;  ; E_s=2,06; =2,495м.

.

2)  проверка условия (3.39) над второй опорой.

A_s=0,02443 м; ; E_s=2,06; =2,789м.

.

Кроме проверки на раскрытие трещин в растянутой зоне, необходим расчёт, по которому не допускается образование продольных трещин, совпадающих с направлением действия нормальных сжимающих напряжений. Для изгибаемых элементов расчёт проводится по формуле

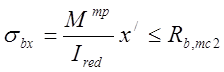,                                          (3.41)

где  - изгибающий момент при расчёте на трещиностойкость;  - приведённый момент инерции; x’ – высота сжатой зоны по формуле (3.28); R_b,mc2 = 19,6МПа – расчётное сопротивление бетона осевому сжатию [3, 3.24].

1)  проверка середины среднего пролёта.

x’=0,386м; =0,1873;

     .

2) проверка над опорой.

x’=0,487м; =0,25747;

     .

В обоих случаях проверки проходят с хорошим запасом.

3.10. Расчёт на вертикальный прогиб.

Прогиб балок пролётных строений вычисляют методами строительной механики. Вертикальные прогибы пролётных строений, вычисленные при действии подвижной временной нагрузки, не должны превышать для железнодорожных мостов величины .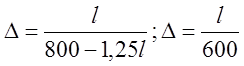

Величину вертикального прогиба допускается вычислить по формуле

        ,

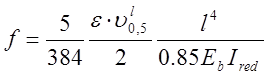где E_b – модуль упругости бетона [3, п.3.32]. Полученный по расчёту прогиб должен быть меньше предельного прогиба. Остальные значения см. п.3.2, 3.31, 3.7.

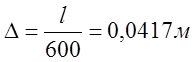           и .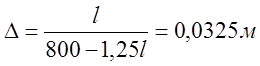

После вычислений <.

Выводы: все выше перечисленные проверки для главной балки проходят, следовательно, запроектированное пролётное строение удовлетворяют всем нормам, а значит можно приступать к окончательному конструированию моста.

4.Расчёт устоя моста.

4.1.Определение расчётных усилий.

Для расчёта принят необсыпной  устой, применённый при разработке первого варианта путепровода.

Расчёт проводится по одной схеме: загружение пролёта с призмой обрушения.[3,прил.5.,п.6, пп.2.1-2.3, прил.2] (рис.4.1), но силы, возникающие от торможения подвижного состава, попеременно направим в сторону пролёта и в сторону устоя.

Схема 1.

Рис.4.1. Расчётная схема для расчёта устоя путепровода.