Проектирование железобетонного моста под железную дорогу через водоток в Сибири, страница 7

Производится проверка на прочность и на выносливость вручную, а затем дополнительно делается проверка на ЭВМ.

3.1. Построение линий влияния внутренних усилий в главной балке

Для расчёта неразрезной балки необходимо построить линии влияния: для первого пролёта – М(0), М(0,5), М(0,75), Q(0); для второго пролёта - М(0), М(0,25), М(0,5), Q(0), Q(0,25) и Q(0,5).

Линии влияния изображены на рис. 3.1, 3.2, 3.3, 3.4. При этом использовался метод перемещений и, частично, метод конечных элементов (для построения и нахождения площадей линий влияния М(0,5), М(0,75) для первого пролёта использовалась программа POLUPROM (INTAB13)).

 При устройстве пути на балласте эквивалентные нагрузки во всех формулах определяются при =0,5 независимо от положения вершин линий влияния.

3.2. Определение нагрузок

Все нагрузки постоянные или временные считаются равномерно распределенными вдоль моста.

Постоянные нагрузки от собственного веса определяются по формуле:

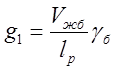,                                              (3.1)

где  = 68 м - объем железобетона пролетного строения, определяемый в зависимости от расчетной длины пролетного строения [1, табл. п.1.1], равный;  = 24,5 kH/м - удельный вес бетона равный;  = 25 м - расчетная длина пролетного строения равная.

Из формулы (3.1) вычислено:

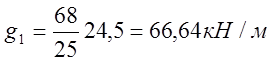
Нагрузка от балласта определяется по формуле:

,                                             (3.2)

где  = 19,6 kH/м - удельный вес балласта.

Из формулы (3.2) определено:

Нагрузка от тротуара  = 4 kH/м и нагрузка от перил  = 0,7kH/м величины постоянные.

Временные нагрузки (С13) определяются от подвижного состава [3, прил.5] при =0,5 с помощью интерполяции:

 kH/м – (=l).

 kH/м – (=0,75 l).

kH/м – (=0,5 l).

3.3. Определение расчетных усилий.

3.3.1. Определение коэффициентов для нагрузок.

Коэффициенты надежности по постоянным нагрузкам и по весу балласта определяются в соответствии с [3 п.2.10] и равны:

(=1,2,3,4)=1,1.

Коэффициент надежности по нагрузке  к временным вертикальным нагрузкам принят в соответствии с [3 п.2.23], определен по интерполяции в зависимости от длины загружения  и равен:

.

Динамические коэффициенты определены в соответствии с [3 п.2.22] в зависимости от

; ; .

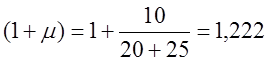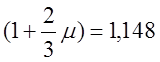 - коэффициент учитывающий наличие в поездах только перспективных локомотивов и вагонов, а также отсутствие тяжелых транспортеров; определен для  в соответствии с [3 п.2.11].

Рис.3.5. Схемы загружения линий влияния неразрезной балки.

3.3.2. Усилия для расчетов на прочность.

Определяем усилия для второго пролёта.

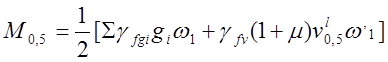,                           (3.3)

где ,  - коэффициенты надежности по постоянным и временным нагрузкам (п.6.3.1);  = 30,9 - площадь линии влияния для  для постоянных нагрузок (п.6.1);  = 37,44 - площадь линии влияния  для переменной нагрузки.

Из формулы (3.3) определено:

.

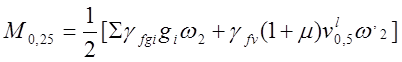,                           (3.4)

где  = 12,42 - площадь линии влияния  для постоянных нагрузок (п.3.1);  - площадь линии влияния  для переменных нагрузок (п.3.1).

.

,

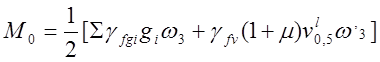где - площадь линии влияния  для постоянных нагрузок (п.3.1);  - площадь линии влияния  для переменных нагрузок (п.3.1).

   = 3808,4 кНм.

Поперечная сила определяется по формуле

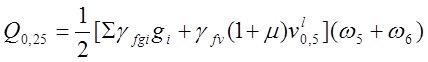,                         (3.5)

где ,  - площади линии влияния для  равные 8,9227 и (-0,604) соответственно.

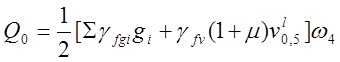,                                (3.6)

где  = 12,5 м- площадь линии влияния для .

Из формулы (3.6) определено:

.

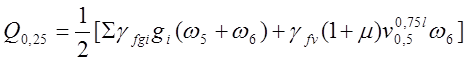,                       (3.7)

где  - коэффициент надежности по временной нагрузке;  - динамический коэффициент;  - нагрузка от подвижного состава для , равная 170,91 kH/м.

Из формулы (3.7) определено:

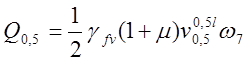,                                      (3.8)

где  - коэффициент надежности по временной нагрузке;  - динамический коэффициент;  = 189,12 kH/м - нагрузка от подвижного состава для ;  = 2,781 м - площадь линии влияния для .

Из формулы (3.8) вычислено:

.

По выше изложенным формулам производим подсчёт усилий для первого пролёта.

 kH/м – (=l).

 kH/м – (=0,75 l).

kH/м – (=0,5 l).

.

.

=0 кНм.

.

кН.

Все выше найденные усилия являются максимальными положительными. Для построения огибающей эпюры неразрезной балки необходимо также определить максимальные отрицательные усилия. Для этих расчётов необходимы наибольшие отрицательные площади. Площади показаны на рис.3,1-3,4.

Max “-“  - для первого пролёта.

Для второго пролёта определяется несколько усилий:

·  max “-“ =8723,6 кНм;

·  max “-“ .

3.3.3. Усилия для расчетов на выносливость.

Значения площадей линий влияния смотри п.3.1, коэффициентов – п.3.3.1, постоянных и временных нагрузок – п.3.2.

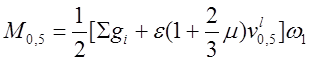,                                 (3.9)

Из формулы (3.9) рассчитано:

.

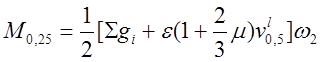,                                (3.10)

Из формулы (3.10) вычислено:

.

,

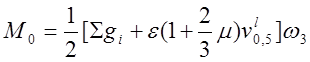откуда

3.3.4. Усилия для расчетов на трещиностойкость.

·  по образованию продольных трещин:

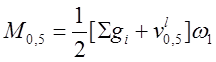,                                        (3.11)

;

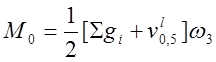
·  по раскрытию нормальных трещин

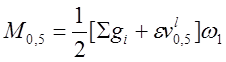,                                      (3.12)

;

;

.

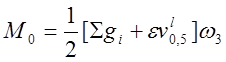·  по ограничению касательных напряжений

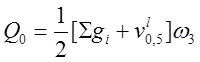,                                         (3.13)

;

·  по раскрытию наклонных трещин

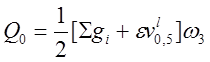,                                        (3.14)

.

3.4. Назначение расчетного сечения балки и подбор рабочей арматуры в середине пролета.

В виду того, что сечение балки сложное, исходное сечение приводится к расчетному, более простому. Борта балластного корыта при этом не учитываются. Полка переменной толщины заменяется полкой постоянной толщины без вутов.

Приведенная толщина плиты:

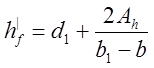,                                           (3.15)

где =0,14 м - исходная толщина плиты;  = 2,08 м - исходная ширина плиты балластного корыта;  = 0,24 м - толщина ребра;  - площадь вутов (радиус одного вута равен 0,3м), равная:

 (м).

По формуле (3.15) вычислено:

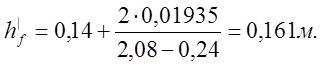
Площадь сечения консолей определена по формуле:

,                                          (3.16)

где , , ,  - смотри 3.15