Строительство и архитектура \ Проектирование мостов

Проектирование железобетонного моста под железную дорогу через водоток в Сибири, страница 6


Рис. 2.3. Расчётное сечение консольной части плиты.

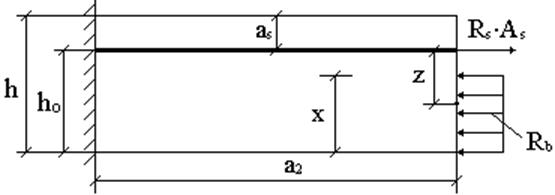
h = 0,3×0,3 + 0,14 = 0,23 м

hо = 0,23 – 0,026 = 0,204 м

z = 7×0,204/8 = 0,1785 м

As ³ М/(Rs×z) = 55,456/(250×178,5) = 12,43 см²

Количество стержней должно находиться в пределах:7 £ n £ 24

n ³ Аs/Ао = 12,43/1,13 = 11,0.

2.5. Расчёт нормального и наклонного сечения плиты.

2.5.1. Расчёт на прочность.

2.5.1.1 Расчёт нормального сечения на прочность.

Проверка на прочность по моменту производится в соответствии с пунктом 3.62 [3].

Расчёт производится из условия:

Мо £ mb7×Rb×b×x×(ho – 0,5×x)                                   (2.18)

где Мо = 55,456 кН×м – внутреннее усилие в сечении; mb7 = 0,9 – коэффициент условий работы, принимаемый по [3] п.3.25; Rb = 20 МПа – расчётное сопротивление бетона сжатию (для В40); b = 1 м – толщина сечения; х – высота сжатой зоны вычисляемая по формуле:

х = (Rs×As)/(mb7×Rb×b)                                        (2.19)

х = (250 × 14,69) / (0,9×20) = 0,0204 м

55,456 кН×м < 20×14,69×(0,204 – 0,5×0,0204) = 60,996 кН×м

Условие выполняется.

2.5.1.2 Расчёт наклонного сечения на прочность.

Расчёт выполняется в соответствии с пунктом.3.81 СНиП 2.05.03-84.

Расчёт производится из условия:

Q £ 1,5×Rbt×b×ho²/c                                          (2.20)

где Rbt = 1,25 МПа – расчётное сопротивление бетона на осевое растяжение; с – проекция наклонного сечения на горизонталь, с=hо=0,204м.

142,196 кН < 1,5×1250×0,204 = 382,5 кН. =>условие выполняется.

2.5.2. Расчёт на выносливость.

Расчёт на выносливость выполняется в соответствии со СНиП п.3.94.

1)Расчёт на выносливость по бетону:

Проверка на выносливость по бетону выполняется из условия

sb¢ = M¢×x¢/Ired £ mb1×Rb                                       (2.21)

где sb¢ – напряжение в бетоне; Ired – момент инерции приведённого сечения относительно его центра тяжести; х¢ – высота сжатой зоны бетона; mb1 – коэффициент условий работы.

х¢ = n¢×As×{Ö[1 + (2×b×ho)/(n¢×As)] – 1}/b                       (2.22)

где  n¢ = 10 – отношение модулей упругости принимаемое по СНиП п.3.48.

Ired = (b×x¢³/3) + [n¢×As×(ho – x¢)²]                           (2.23)

х¢ = 10×14,69×{Ö[1 + (2×2040)/(10×14,69)] – 1}/10000 = 0,0641 м

Ired = 1×0,0641³/3 + [10×14,69(0,204 – 0,0641)²] = 0,3753 × 10‾³ м

mb1 = 0,6 × bb × eb                                           (2.24)

где bb = 1,26 – коэффициент, учитывающий рост прочности бетона во времени (3, п.3.26); eb – коэффициент, зависящий от коэффициента асимметрии цикла rb (3, п.3.26):

rb = Мр/(Мр + Мq)                                            (2.25)

где Мр = 4,024 кН×м – момент на выносливость от постоянных нагрузок;                    (Мр + Мq) = 38,509 кН×м – момент на выносливость от постоянных и временных нагрузок

rb = 4,024/38,509 = 0,1045 Þ eb = 1,005.

mb1×Rb = 0,6×1,26×1,005×20000 = 15195,6 кПа

sb¢ = 38,509×10³×0,0641/0,3753×10‾³ = 6872,3 кПа < 15195,6 кПа

Условие выполняется.

2) Расчёт на выносливость по арматуре:

Проверка на выносливость по арматуре выполняется из условия

ss¢ = n¢×M¢×(h – x¢)/Ired £ mas1×Rs                              (2.26)

где ss¢ – напряжение в арматуре; mas1 – коэффициент условий работы арматуры по СНиП п.3.39

mas1 = brw × ers,                                             (2.27)

где brw = 1 – коэффициент, учитывающий влияние на условия работы арматурных элементов наличия сварных стыков; ers - коэффициент, зависящий от коэффициента асимметрии цикла r;

r = rb = 0,1045 Þ ers = 0,702.

mas1×Rs = 1×0,702×250000 = 175000 кПа

ss¢ = 10×38,509×(0,204–0,0641)/0,3753×10‾³=168187 кПа < 175000 кПа

Условие выполняется.

2.5.3. Расчёт на трещиностойкость.

Расчёт на трещиностойкость выполняется в соответствии со СНиП п.3.105.

Расчёт по раскрытию продольных трещин выполняется из условия:

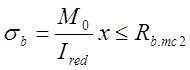     ,                                              (2.28)

где х = 0,047 м; Ired = 1,85 - высота сжатой зоны и момент инерции, рассчитываемые по формулам 2.22 и 2.23 с новым значением n;

n = 5,72 - отношение модулей упругости стали и бетона (3, п. 3.48).

 - расчётное сопротивление осевому сжатию на стадии эксплуатации (3, п.3.24).

.

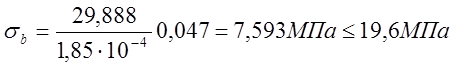Условие (2.28) выполняется.  

Расчёт по раскрытию нормальных трещин выполняется из условия:

аcr = ss×y/Es £ 0,02см                                       (2.29)

где аcr – величина раскрытия трещины; ss – напряжения в арматуре;                            Еs = 206000 МПа – модуль упругости арматуры; y – коэффициент раскрытия трещин; 0,02 см – допустимая величина раскрытия трещин;

ss = n×Mтр×(hо – x)/Ired,                                      (2.30)

где n = 5,72 - отношение модулей упругости стали и бетона (3, п. 3.48).

х = 0,047 м;

Ired = 1,85.

ss = 5,72× 29,888×(0,204 – 0,047)/ 1,85 = 145,08 МПа

y=  - коэффициент раскрытия трещин для стержневой арматуры периодического профиля                                          (2.31)

где Rr – радиус взаимодействия бетона с арматурой;

Rr = Аr/(åb × n × do)

где Аr – площадь зоны взаимодействия для нормального сечения; b = 1 – коэффициент зависящий от расстановки арматуры для одиночных стержней; n = 13 – число арматурных стержней; dо = 12 мм – диаметр арматуры:

Аr = b×(do/2 + 2см + 6×do); (все величины в см)               (2.32)

Аr = 100×(1,2/2 + 2 см + 6×1,2) = 980 см².

Rr = 980/(1×13×1,2) = 62,82 см.

y = .

аcr = 145,08×11,9/206000 = 0,0084 см < 0,02 см

Условие (2.29) выполняется.

После выполнения ручного расчёта производим компьютерную проверку,  результаты которой представлены в приложении 2.

3.Расчёт главной балки пролётного строения.

Для расчета принимается неразрезная балка из обычного железобетона с расчетными пролетами 17,5+25+17,5 м.

Для построение линий влияния и нахождения их площадей данным студентом разработана программа в среде Microsoft Excel.

Скачать файл