ω=0,85-0,008·14,3=0,736;
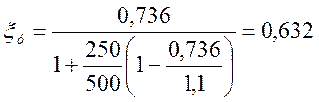
0,449 < 0,632·1,95=1,232
![]() (3.20)
(3.20)
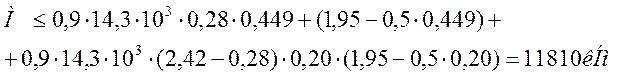
М=11590 кНм<11810кНм
Условие выполняется.
Расчет балки на выносливость в середине пролета.
Должно выполнятся следующее условие:
а) по бетону
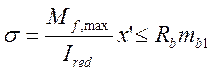 ; (3.25)
; (3.25)
где ![]() -
коэффициент условий работы
-
коэффициент условий работы
βb= 1,34– коэффициент, учитывающий рост прочности бетона во времени
εb– коэффициент, зависящий от асимметрии цикла повторяющихся напряжений.
Rb – расчетное сопротивление бетона
x΄- высота сжатой зоны, находится из условия равенства нулю статического момента всего сечения относительно нейтральной оси
![]() ,
(3.26)
,
(3.26)
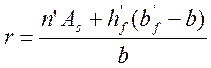 ;
(3.27)
;
(3.27)
где n΄=17 – отношение модулей упругости арматуры и бетона с учетом виброползучести бетона.
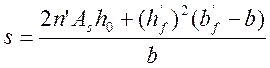 ; (3.28)
; (3.28)
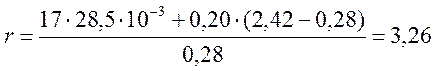 м
м
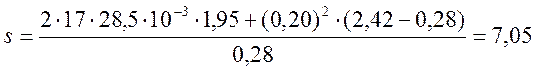 м
м
![]()
Приведенный момент инерции будет равен:
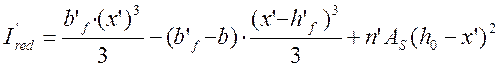 ; (3.29)
; (3.29)
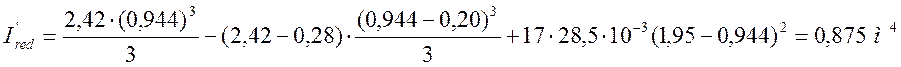
Для определения расчетных сопротивлений бетона и арматуры на выносливость необходимо знать максимальные и минимальные значения напряжений в них для определения характеристик цикла повторяющихся напряжений:
pb=σb,min/σb,max
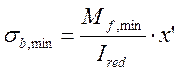
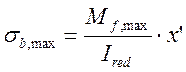
Где Mf,max и Mf,min – изгибающие моменты для расчетов на выносливость, равные 9,461 МПа и 4,051 МПа соответственно.
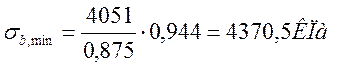
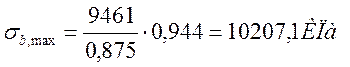
pb=4370,5/10207,1=0,43
εb=1,165
![]()
![]() кПа
кПа
Напряжение в бетоне:
10207,1<13399,1
Условие выполняется.
б) по арматуре
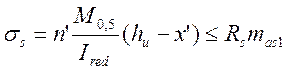 ; (3.30)
; (3.30)
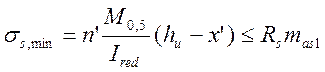
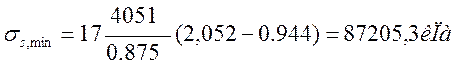
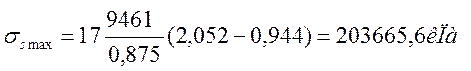
pb=87205,3/203665,6=0,43
где ![]() - коэффициент условий
работы арматуры;
- коэффициент условий
работы арматуры;
βpw=1– при контактной сварке с механической зачисткой стыка по п.3.39 [1];
εps=0,895;
![]() =17 - отношение модулей упругости
арматуры и бетона;
=17 - отношение модулей упругости
арматуры и бетона;
![]() =9461кНм;
=9461кНм;
hu=2,052 м.
![]() = 0,875
= 0,875![]()
![]()
![]()
![]() кПа
кПа
203665,6<223700
Расчет балки на трещиностойкость в середине пролета.
По раскрытию трещин:
Должно выполнятся следующее условие:
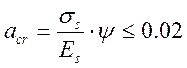 см;
(3.31)
см;
(3.31)
где σs- напряжение в арматуре, равное 185100 кПа;
Еs = 2,06×![]() МПа – модуль упругости арматуры
МПа – модуль упругости арматуры
![]() - коэффициент раскрытия трещин
- коэффициент раскрытия трещин
Rr- радиус армирования равный
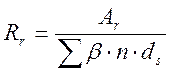 ;
(3.32)
;
(3.32)
где Аr- площадь взаимодействия по п 3,110 [2]
![]() ;
(3.33)
;
(3.33)
где аs – расстояние от оси арматурных стержней до растянутой зоны, равное 0,15;
b =0,85 – коэффициент, учитывающий степень сцепления арматурных элементов с бетоном по п 3.110 [2]
Аr = 56×(15+6×3,6) = 2049,6
![]()
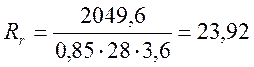 см
см
![]()
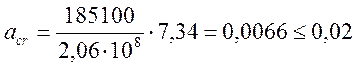
Условие выполняется.
На образование продольных трещин:
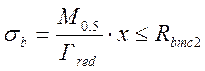 ;
(3.35)
;
(3.35)
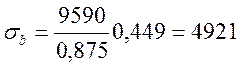 кПа
кПа
![]() кПа
кПа
4921<13200
Условие выполняется.
Построение эпюры материалов с определением мест отгибов рабочей арматуры.
Для определения мест отгибов рабочей арматуры строим огибающую эпюру максимальных моментов в балке.
Начало отгибов продольных растянутых стержней арматуры располагаем за сечением, в котором стержни учитываются с полным расчётным сопротивлением. Длину заводки за сечение для арматуры стали класса АII и бетона класса В27,5 определяем по формуле:
(2.60)
Построение эпюры материалов, а также определение мест отгибов рабочей арматуры ведём в соответствии с требованиями [2]:
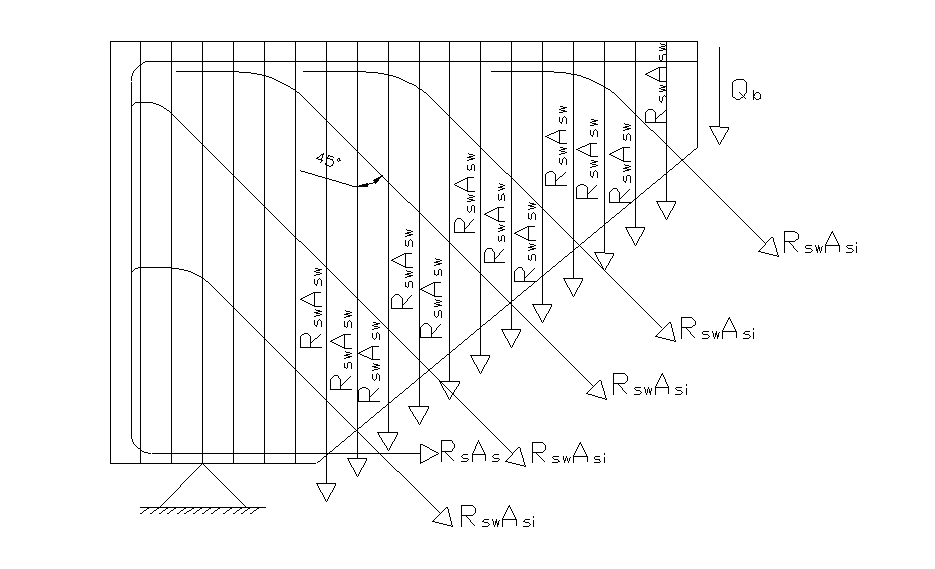
Рис. 3.6 Схема для расстановки наклонных стержней.
Расчёт на прочность наклонных сечений главной балки.
1. Расчёт на прочность по сжатому бетону между наклонными трещинами:
![]() (2.61)
(2.61)
где Q - поперечная сила на расстоянии не ближе h0 от оси опоры, Q=1354кН;
![]() = 1 + ηn1Asw/(bSw), при расположении хомутов нормально к
продольной оси
= 1 + ηn1Asw/(bSw), при расположении хомутов нормально к
продольной оси
![]() ≤1,3;
≤1,3;
η =5 – при хомутах, нормальных к оси элемента;
n1 – отношение модулей упругости арматуры и бетона (п. 3.48 [2]), n1=7,94;
Asw – площадь сечения ветвей хомутов, расположенных в одной плоскости Asw=2·3,14·0,012/4=1.57·10-4 м2;
Sw – расстояние между хомутами по нормали к ним, Sw=0.15м;
![]() - толщина стенки (ребра) главной
балки;
- толщина стенки (ребра) главной
балки;
![]() = 1 – 0,01Rb –
коэффициент. Здесь Rb принимаем в МПа,
= 1 – 0,01Rb –
коэффициент. Здесь Rb принимаем в МПа, ![]() =1-0,01·14,3=0,857;
=1-0,01·14,3=0,857;
![]() - рабочая высота сечения,
- рабочая высота сечения, ![]() =1,95м.
=1,95м.
![]() = 1 +5·7,94·0,000157/(0,28·0,15)=1.15
= 1 +5·7,94·0,000157/(0,28·0,15)=1.15
Условие выполняется.
2. Расчёт наклонного сечения на действие поперечной силы:
![]() (2.62)
(2.62)
где ![]() - максимальное значение
поперечной силы от внешней нагрузки, расположенной по одну сторону от
рассматриваемого наклонного сечения;
- максимальное значение
поперечной силы от внешней нагрузки, расположенной по одну сторону от
рассматриваемого наклонного сечения; ![]() и
и ![]() - суммы проекций усилий всей
пересекаемой арматуры при длине проекции сечения;
- суммы проекций усилий всей
пересекаемой арматуры при длине проекции сечения;![]() -
расчетное сопротивление арматуры с учетом коэффициента ma4:1
-
расчетное сопротивление арматуры с учетом коэффициента ma4:1
![]() ; (2.63)
; (2.63)
![]() МПа;
МПа;
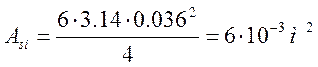
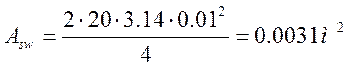
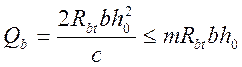 ; (3.37)
; (3.37)
где Rbt= 1,05 МПа – расчетное сопротивление бетона по прочности на сжатие, зависит от класса бетона, по табл. 23 [1]
![]() м
м
m = 2
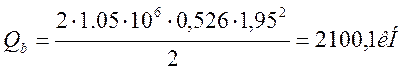
![]()
2100,1 <2154
Принимаем Qb = 2100,1 кН
![]() кН
кН
Q = 1899 (по интерполяции см. лист 2)
1899 < 3289,85
Условие выполняется.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.