где ![]() максимальные напряжения, возникающие
в арматуре при расчёте на трещиностойкость;
максимальные напряжения, возникающие
в арматуре при расчёте на трещиностойкость; ![]() -
коэффициент раскрытия трещин для стержневой арматуры периодического профиля,
определяемый по формуле:
-
коэффициент раскрытия трещин для стержневой арматуры периодического профиля,
определяемый по формуле:
![]() , (2.75)
, (2.75)
где ![]() - радиус
армирования:
- радиус
армирования:
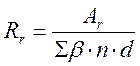 , (2.76)
, (2.76)
где ![]() – площадь зоны взаимодействия для
нормального сечения:
– площадь зоны взаимодействия для
нормального сечения:
![]() , (2.77)
, (2.77)
А –
расстояние от нижнего края балки до центра тяжести верхнего полного ряда
арматуры; ![]() 0,75;
0,75; ![]() 30;
30;
![]() 0,040 м.
0,040 м.
![]() м2;
м2;
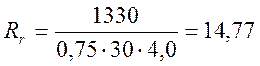 см;
см;
![]() см;
см;
![]() 2,06·105 МПа.
2,06·105 МПа.
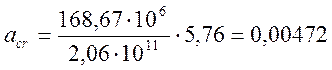 см,
см,
![]() = 0,00472см < 0,02см.
= 0,00472см < 0,02см.
Условие по раскрытию нормальных трещин выполняется.
Т.к. условие выносливости по арматуре не выполняется, то увеличиваем диаметр арматуры до 40мм.
Последующие расчеты производим с этим диаметром. Данные по расчетам представлены в приложении.
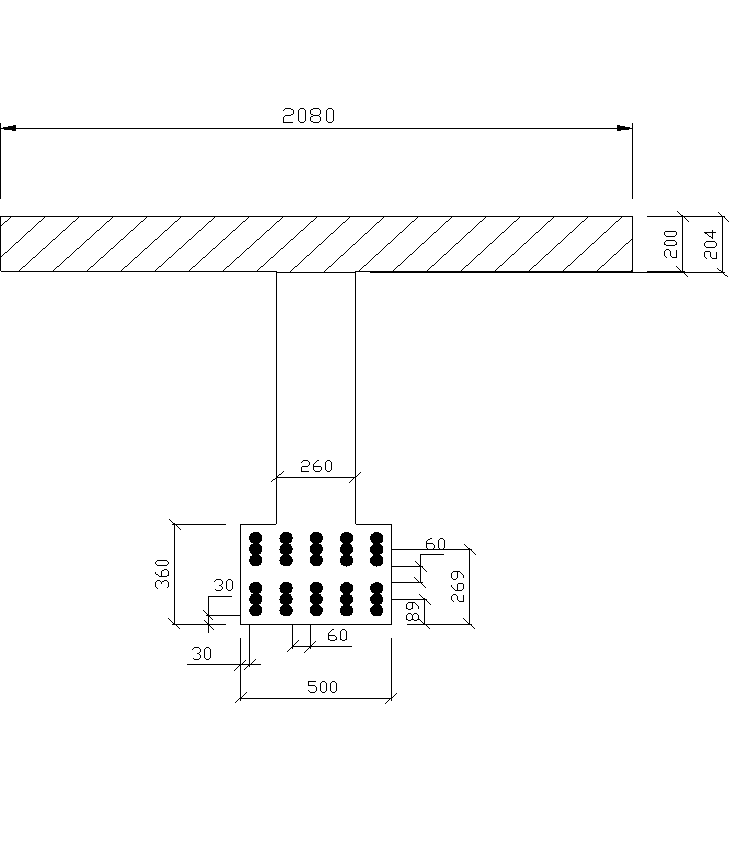
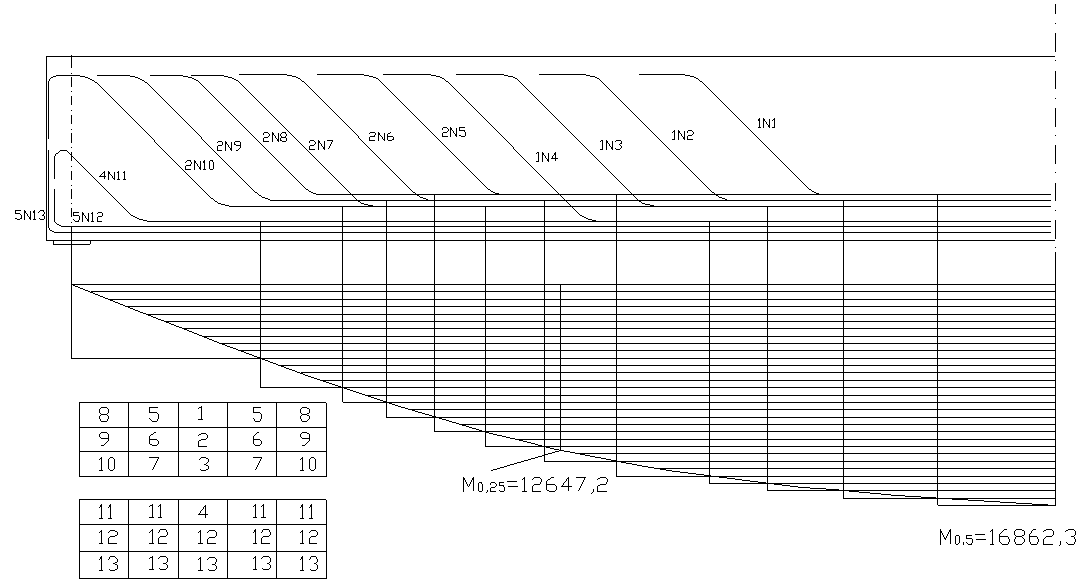
Рисунок 2.6 – Схема расположения арматуры в главной балке
(исправленная)
2.6.8 Построение эпюры материалов с отметкой отгибов рабочей арматуры
Для определения мест отгибов рабочей арматуры строим огибающую эпюру максимальных моментов в балке.
Начало отгибов продольных растянутых стержней арматуры расположено за сечением, в котором стержни учитываются с полным расчетным сопротивлением. Длину заводки за сечение для арматуры стали класса А-II при классе бетона В40 определяем по формуле:
![]() ; (2.78)
; (2.78)
![]() м.
м.
Построение эпюры материалов ведем в соответствии с конструктивными требованиями [1].
 Рисунок
2.7 - Схема для расстановки наклонных
стержней
Рисунок
2.7 - Схема для расстановки наклонных
стержней
2.6.9 Расчет на прочность наклонных сечений главной балки
Образование наклонных трещин при поперечном изгибе происходит в результате совместного действия изгибающего момента и поперечной силы.
1) Расчет прочности сжатого бетона между наклонными трещинами.
Прочность по сжатому бетону между наклонными трещинами обеспечивается исходя из следующего условия:
![]() , (2.79)
, (2.79)
где ![]() - поперечная сила на расстоянии не
больше
- поперечная сила на расстоянии не
больше ![]() от оси опоры,
от оси опоры, ![]() кН;
кН;
![]() - определено по формуле:
- определено по формуле:
![]() , (2.80)
, (2.80)
где ![]() = 5 – при хомутах, нормальных к
продольной оси элемента;
= 5 – при хомутах, нормальных к
продольной оси элемента;
![]() - отношение модулей упругости
арматуры и бетона, определяемое по [1 ,п.3.48];
- отношение модулей упругости
арматуры и бетона, определяемое по [1 ,п.3.48];
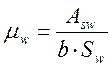 , (2.81)
, (2.81)
где ![]() - площадь сечения ветвей хомутов
(диаметр арматуры в хомутах принимаем - 0,010м=10мм), расположенных в одной
плоскости,
- площадь сечения ветвей хомутов
(диаметр арматуры в хомутах принимаем - 0,010м=10мм), расположенных в одной
плоскости,
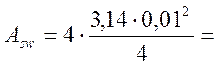 3,14·10-4 м2 ;
3,14·10-4 м2 ;
![]() м - расстояние между хомутами по
нормали к ним;
м - расстояние между хомутами по
нормали к ним;
![]() м - толщина ребра;
м - толщина ребра;
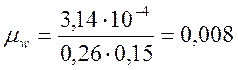 ;
;
![]() ;
;
![]() 2,33 м - рабочая высота
сечения;
2,33 м - рабочая высота
сечения;
![]() ; (2.82)
; (2.82)
![]() ;
;
![]() ;
;
1874,53 кН < 4071 кН - Условие выполняется.
2) Расчет наклонного сечения на действие поперечной силы.
Расчет производим исходя из условия:
![]() , (2.83)
, (2.83)
где ![]() - максимальное значение поперечной
силы от внешней нагрузки, расположенной по одну сторону от рассматриваемого
наклонного сечения;
- максимальное значение поперечной
силы от внешней нагрузки, расположенной по одну сторону от рассматриваемого
наклонного сечения;
![]() и
и ![]() -
суммы проекций усилий всей пересекаемой арматуры при длине проекции сечения
-
суммы проекций усилий всей пересекаемой арматуры при длине проекции сечения ![]() м;
м;
![]() - расчетное сопротивление арматуры с
учетом коэффициента ma4:
- расчетное сопротивление арматуры с
учетом коэффициента ma4:
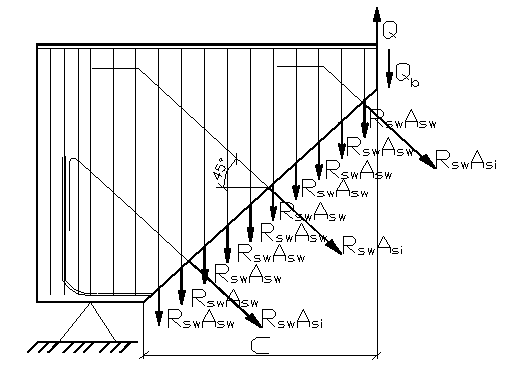
Рисунок 2.8 – Схема для расчета прочности наклонного сечения на действие поперечной силы
![]() ; (2.84)
; (2.84)
![]() МПа;
МПа;
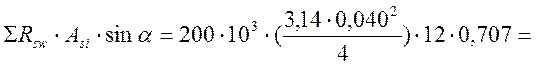 2308,78 кН;
2308,78 кН;
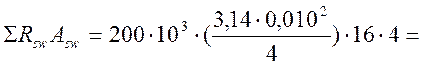 942 кН;
942 кН;
![]() - поперечное усилие, передаваемое в
расчете на бетон сжатой зоны над концом наклонного сечения и определяемое по
формуле:
- поперечное усилие, передаваемое в
расчете на бетон сжатой зоны над концом наклонного сечения и определяемое по
формуле:
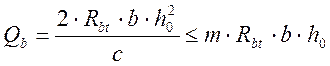 ; (2.85)
; (2.85)
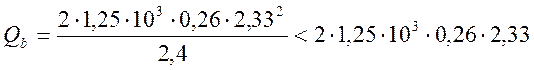 кН;
кН;
1470,33 < 1514,5;
Принимаем ![]() кН;
кН;
2507,44 кН < 2308,78 + 942 + 1470,5 кН
2507,44 кН < 4721,28 кН - Условие выполняется.
2.6.10 Расчет наклонного сечения по раскрытию трещин
Железобетонные
балки с ненапрягаемой арматурой должны удовлетворять категории требований по
трещиностойкости. Максимальные растягивающие напряжения ![]() в
поперечной и продольной арматуре определяем по формуле:
в
поперечной и продольной арматуре определяем по формуле:
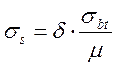 , (2.86)
, (2.86)
где ![]() - напряжение в балке, равное
касательному напряжению
- напряжение в балке, равное
касательному напряжению ![]() на уровне центра
тяжести сечения:
на уровне центра
тяжести сечения:
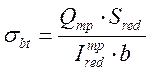 , (2.87)
, (2.87)
где ![]() - поперечная сила, определяемая по
интерполяции на расстоянии (2ho + 0,35);
- поперечная сила, определяемая по
интерполяции на расстоянии (2ho + 0,35);
![]() - статический момент отсеченной
части сечения;
- статический момент отсеченной
части сечения;
![]() - приведенный момент инерции
сечения;
- приведенный момент инерции
сечения;
![]() - коэффициент армирования стенки на
участке наклонной трещины по направлению главных растягивающих напряжений:
- коэффициент армирования стенки на
участке наклонной трещины по направлению главных растягивающих напряжений:
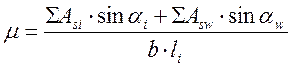 , (2.88)
, (2.88)
![]() -
коэффициент, учитывающий перераспределение напряжений в зоне образования наклонных
трещин, определяемый по формуле:
-
коэффициент, учитывающий перераспределение напряжений в зоне образования наклонных
трещин, определяемый по формуле:
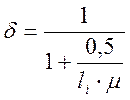 , (2.89)
, (2.89)
где ![]() - длина, см, предполагаемой
наклонной трещины по направлению, перпендикулярному главным растягивающим
напряжениям на участке между вутами поясов.
- длина, см, предполагаемой
наклонной трещины по направлению, перпендикулярному главным растягивающим
напряжениям на участке между вутами поясов.
Произведем вычисления:
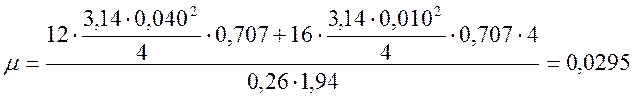 ;
;
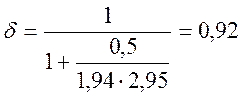 ;
;
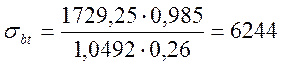 кПа;
кПа;
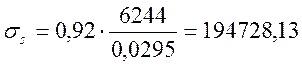 кПа;
кПа;
По условию (2.73) определяем радиус армирования по формуле:
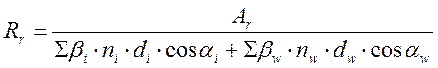 , (2.90)
, (2.90)
где площадь зоны взаимодействия вычисляем по формуле:
![]() , (2.91)
, (2.91)
![]() см2;
см2;
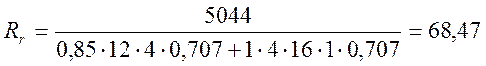 см;
см;
![]() см;
см;
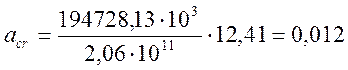 см;
см;
0,012 см < 0,02 см.
Условие по раскрытию трещин наклонного сечения выполняется.
Контроль вычислений производим на ЭВМ, результаты отображаем в приложении.
2.7 Расчет необсыпного устоя
В данном курсовом проекте принимаем к расчету обсыпной массивный бетонный устой, запроектированный по второму варианту. Ширина по высоте устоя остается постоянной (3,8 м), тротуары вынесены на консоли.
2.7.1 Определение нагрузок
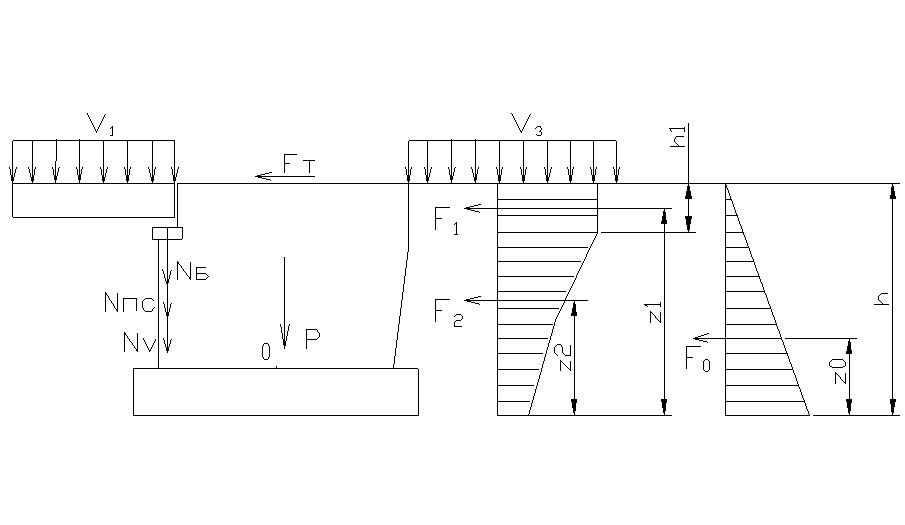
Рисунок 2.9 – Схема загружения устоя.
Постоянные нагрузки:
- Нагрузку от собственного веса устоя определяем при помощи ЭВМ с применением программного пакета «AutoCad-2005» по формуле:
![]() , (2.92)
, (2.92)
где V – объем всего устоя, V = 170,5 м3; ![]() =
24 кН/м3 – удельный вес бетона.
=
24 кН/м3 – удельный вес бетона.
![]() кН.
кН.
Положение центра тяжести устоя и точка приложения силы Р вычисляем при помощи ЭВМ.
- Нагрузка от веса пролетного строения. На устой опирается пролетное строение длиной 13,5 м, весом блока 373 кН с тротуарами и перилами общим весом 132,3 кН:
![]() (2.93)
(2.93)
![]() кН.
кН.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.