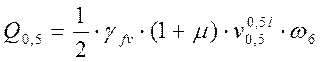 , (2.41)
, (2.41)
где ![]() - коэффициент надежности по
временной нагрузке для
- коэффициент надежности по
временной нагрузке для ![]() ,
, ![]() =
1,26;
=
1,26;
![]() - динамический коэффициент для
- динамический коэффициент для ![]() ,
, ![]() =
1,3;
=
1,3;
![]() - нагрузка от подвижного состава для
- нагрузка от подвижного состава для
![]() ,
,
![]() = 186,11 кH/м;
= 186,11 кH/м;
![]() - площадь линии влияния для
- площадь линии влияния для ![]() ,
, ![]() =
3,36 м
=
3,36 м![]() .
.
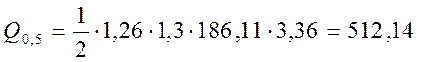 кН.
кН.
2) Усилия для расчетов на выносливость:
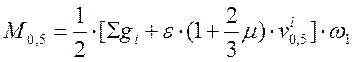 , (2.42)
, (2.42)
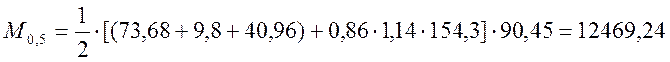 кНм;
кНм;
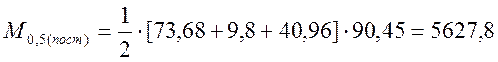 кНм.
кНм.
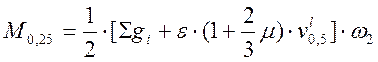 , (2.43)
, (2.43)
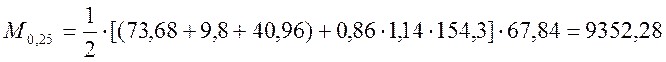 кНм.
кНм.
3) Усилия для расчетов на трещиностойкость:
- по образованию продольных трещин:
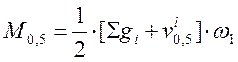 , (2.44)
, (2.44)
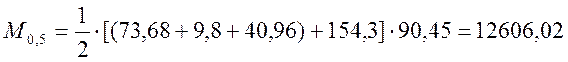 кНм.
кНм.
- по раскрытию нормальных трещин:
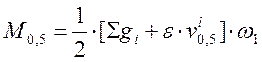 , (2.45)
, (2.45)
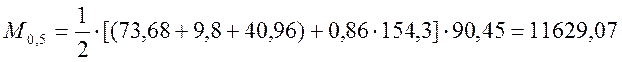 кНм.
кНм.
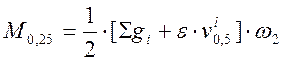 ; (2.46)
; (2.46)
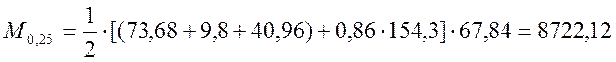 кНм.
кНм.
- по ограничению касательных напряжений:
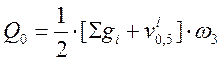 , (2.47)
, (2.47)
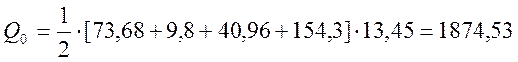 кН
кН
- по раскрытию наклонных трещин:
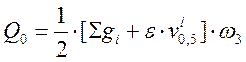 , (2.48)
, (2.48)
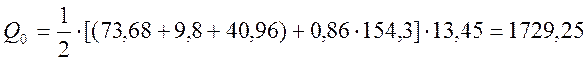 кН.
кН.
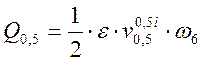 ; (2.49)
; (2.49)
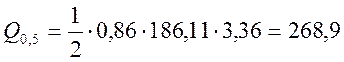 кН.
кН.
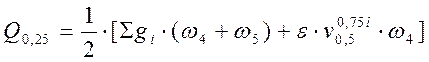 ; (2.50)
; (2.50)
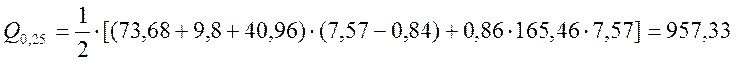 кН.
кН.
Проверку усилий производим на ЭВМ, отчет которой представлен в приложении.
2.6.4 Назначение расчетного сечения главной балки и подбор рабочей арматуры в середине пролета
Исходное сечение главной балки приводим к расчетному. Борта балластного корыта при этом не учитываем, а полку переменной толщины заменяем полкой постоянной толщины без вутов.
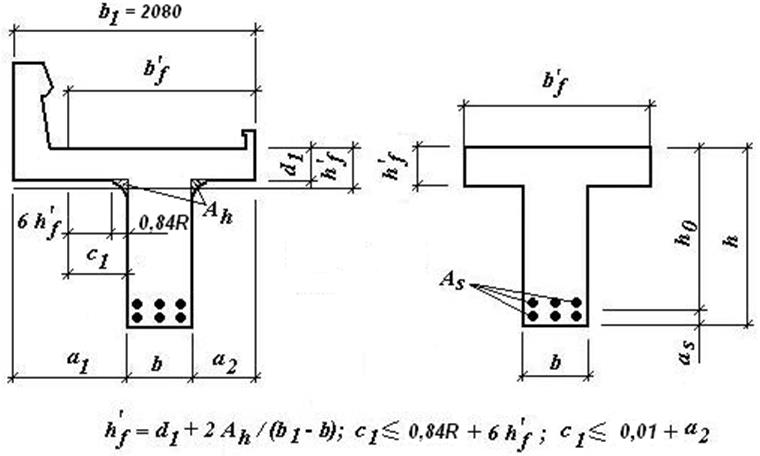
Рисунок 2.4 – Расчетные размеры плиты балластного корыта.
Приведенную толщину плиты вычисляем по формуле:
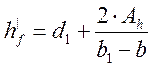 , (2.51)
, (2.51)
где ![]() - исходная толщина плиты, равная 0,18 м;
- исходная толщина плиты, равная 0,18 м;
![]() - исходная ширина плиты балластного
корыта равная 2,08 м;
- исходная ширина плиты балластного
корыта равная 2,08 м;
![]() - толщина ребра равная 0,5 м;
- толщина ребра равная 0,5 м;
![]() - площадь вута, определена по формуле
и равна:
- площадь вута, определена по формуле
и равна:
![]() м2.
м2.
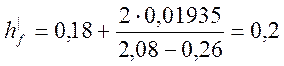 м.
м.
Длину свесов определяем из условия:
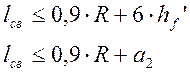 ; (2.52)
; (2.52)
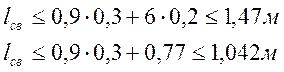
Принимаем ![]() м.
м.
Требуемую
площадь всей арматуры в растянутой зоне приближенно определяем по изгибающему
моменту на прочность ![]() по следующей формуле:
по следующей формуле:
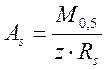 , (2.53)
, (2.53)
где Rs – расчетное сопротивление арматуры класса АII, равное 250 МПа;
z – ориентировочная величина плеча внутренней пары сил, вычисляемая по формуле:
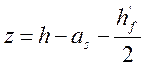 ; (2.54)
; (2.54)
где as=0,15м, [?];
h - высота балки, h=2,5м.
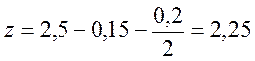 м;
м;
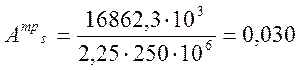 м2.
м2.
Количество стержней арматуры определяем по формуле:
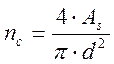 , (2.55)
, (2.55)
где d – диаметр арматуры принимаем равным 36 мм.
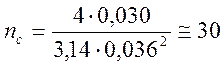 .
.
Фактическое значение площади всей арматуры в растянутой зоне будет равно:
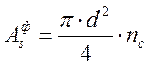 , (2.56)
, (2.56)
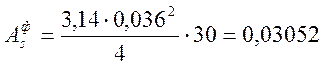 м2.
м2.
Схему расположения арматуры составляем с учетом требований п.3.122 [1]. Данная схема приведена на рисунке 2.5.
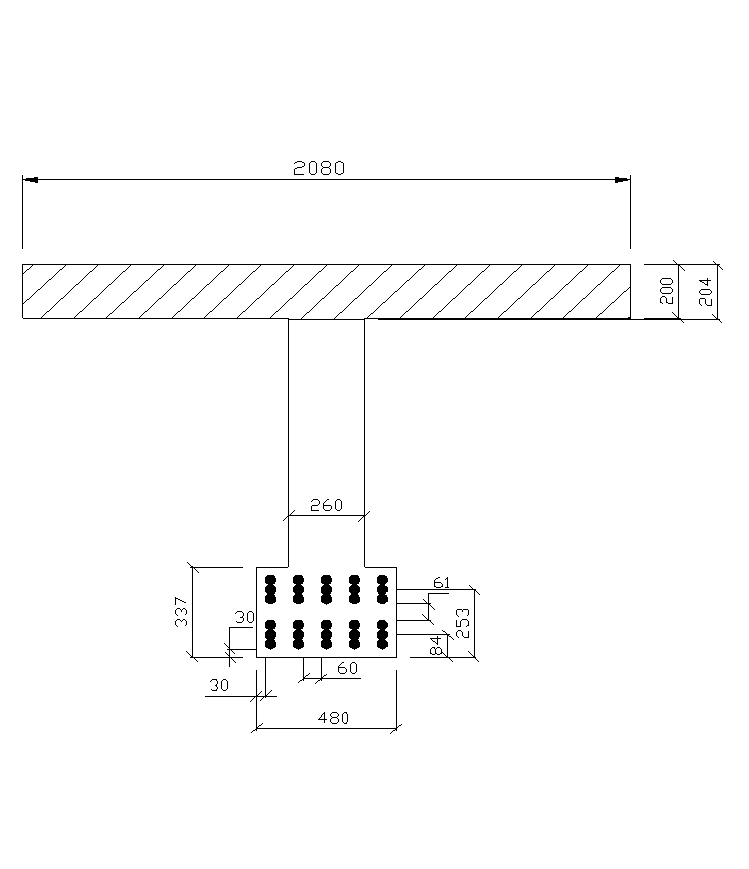
Рисунок 2.5 – Схема расположения арматуры в главной балке
2.6.5 Расчет балки на прочность в середине пролета
Высоту сжатой зоны бетона определяем исходя из следующего условия:
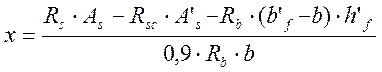 ; (2.57)
; (2.57)
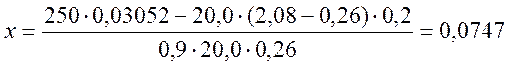 м;
м;
так как ![]() то b=bf’,
пересчитаем высоту сжатой зоны:
то b=bf’,
пересчитаем высоту сжатой зоны:
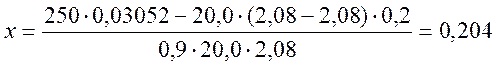 м;
м;
Далее определяем относительную высоту сжатой зоны:
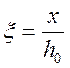 ,
(2.58)
,
(2.58)
где hо – полезная высота сечения, вычисляемая:
![]() , (2.59)
, (2.59)
где ![]() - расстояние от нижней грани до
центра тяжести рабочей арматуры, определяемая:
- расстояние от нижней грани до
центра тяжести рабочей арматуры, определяемая:
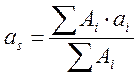 , (2.60)
, (2.60)
где ![]() - площадь i-го стержня;
- площадь i-го стержня; ![]() - расстояние до i-го стержня.
- расстояние до i-го стержня.
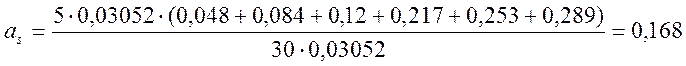 м;
м;
![]() м;
м;
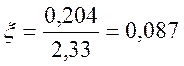 .
.
Относительная высота сжатой зоны должна находиться в следующих пределах:
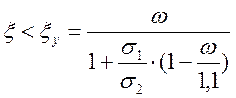 , (2.61)
, (2.61)
где ![]() - характеристика бетона,
определяемая по формуле:
- характеристика бетона,
определяемая по формуле:
![]() , (2.62)
, (2.62)
![]() ,
,
![]() - напряжение в арматуре, 250 МПа;
- напряжение в арматуре, 250 МПа;![]() - предельное напряжение в арматуре
сжатой зоны, 500 МПа.
- предельное напряжение в арматуре
сжатой зоны, 500 МПа.
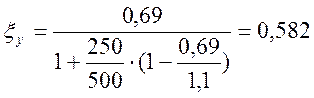 ;
;
0,087 < 0,582 - Условие выполняется.
Далее определяем несущую способность сечения по следующей формуле:
![]() , (2.63)
, (2.63)
![]()
16862,3кН < 18907,7 кН - Условие прочности выполняется.
2.6.6 Расчет на выносливость нормального сечения в середине пролета
Расчет балки на выносливость сводим к ограничению напряжений в бетоне и арматуре соответствующими расчетными сопротивлениями. Условие выносливости нормального сечения имеет вид:
![]() и
и ![]() . (2.64)
. (2.64)
а) проверка бетона на выносливость:
Определяем асимметрию цикла повторяющихся напряжений по следующей формуле:
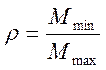 , (2.65)
, (2.65)
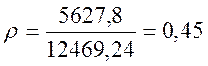 .
.
Определяем высоту сжатой зоны бетона:
![]() , (2.66)
, (2.66)
где r и s вычислим по следующим формулам:
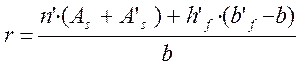 , (2.67)
, (2.67)
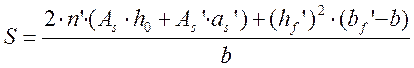 , (2.68)
, (2.68)
Вычисляем:
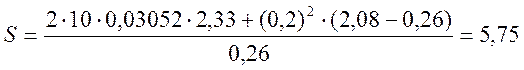 м2;
м2;
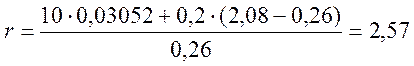 м;
м;
![]() м.
м.
Приведенный момент инерции сечения вычислим по формуле:
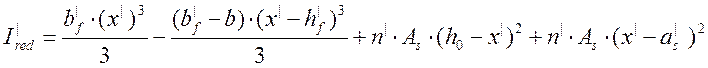 , (2.69)
, (2.69)
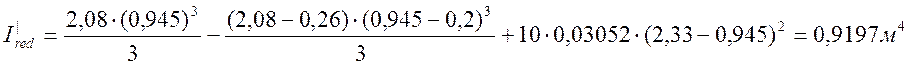
Определяем наибольшие напряжения в бетоне по следующей формуле:
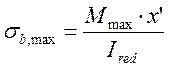 , (2.70)
, (2.70)
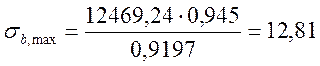 МПа.
МПа.
Расчетное сопротивление бетона на выносливость вычисляем по следующей формуле:
![]() , (2.71)
, (2.71)
где ![]() ,
, ![]() определяем
для
определяем
для ![]() [1, п.3.26, ].
[1, п.3.26, ].
![]() =1,26;
=1,26;
![]() =1,175.
=1,175.
![]() мПа.
мПа.
Исходя из условия 2.63, получаем:
12,81 мПа < 17,76 мПа - Условие выносливости по бетону выполняется.
б) проверка арматуры на выносливость:
Напряжения в арматуре вычисляем по формуле:
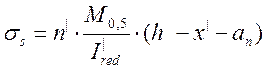 , (2.72)
, (2.72)
где ![]() расстояние от нижней грани балки до
центра тяжести нижнего ряда арматуры,
расстояние от нижней грани балки до
центра тяжести нижнего ряда арматуры, ![]() 0,084м.
0,084м.
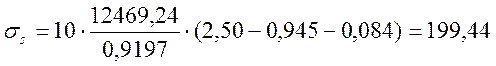 МПа.
МПа.
Расчетное сопротивление арматуры на выносливость определяем по формуле:
![]() , (2.73)
, (2.73)
где ![]() ,
, ![]() -
величины постоянные, определяемые в соответствии [1 ,п.3.39], равные 0,905 и
0,82 соответственно;
-
величины постоянные, определяемые в соответствии [1 ,п.3.39], равные 0,905 и
0,82 соответственно;
![]() - расчетное сопротивление арматуры
класса А-II, равное 250 МПа.
- расчетное сопротивление арматуры
класса А-II, равное 250 МПа.
![]() МПа.
МПа.
199,44 > 185,52 - Условие выносливости по арматуре не выполняется.
2.6.7 Расчет нормального сечения балки на трещиностойкость
Расчет по раскрытию трещин сводим к проверке выполнения условия, ограничивающего ширину раскрытия трещины:
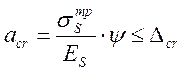 , (2.74)
, (2.74)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.