ss¢ = n¢·M·(hо – x¢)/Ired £ mas1·Rs; (2.26)
где ss¢ – напряжение в арматуре;
mas1 – коэффициент условий работы арматуры по п.3.39 [1]:
mas1 = brw × ers, (2.27)
где brw = 1 – коэффициент, учитывающий влияние на условия работы арматурных элементов наличия сварных стыков;
ers - коэффициент, зависящий от коэффициента асимметрии цикла r:
r = rb = 0,11;
ers = 0,855;
mas1 = 1·0,855 = 0,855;
mas1·Rs = 0,855·200·106 = 171·106 Па;
ss¢ = 10·37,18·103·(0,244 – 0,0664)/4,8996·10-4 = 136,3·106 Па;
136,3 < 171 - Условие выполняется.
2.5.3 Расчет на трещиностойкость
Расчёт на трещиностойкость выполняем в соответствии с п.3.105 [1].
а) Расчёт по раскрытию продольных трещин выполняем из условия:
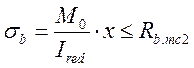 , (2.28)
, (2.28)
где х – высота сжатой зоны бетона, рассчитываемая по формуле 2.22;
Ired - приведенный момент инерции, рассчитываемый по формуле 2.23,
M0 = 29,00 МПа.
Rb,mc2 = 19,6 МПа - расчётное сопротивление бетона осевому сжатию на стадии эксплуатации [1, п.3.24];
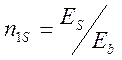 ;
(2.29)
;
(2.29)
где Eb=36·103 МПа – модуль упругости бетона принимаемый по таблице 28 [1];
Es = 2,06·105 МПа - модуль упругости арматуры определяемый по 3.47 [1];
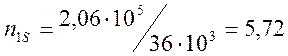
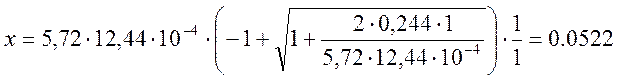 м
м
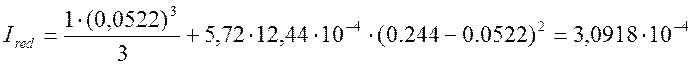 м4.
м4.
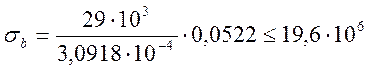 ,
,
4,9 МПа < 19,6 МПа - Условие выполняется.
б) Расчёт по раскрытию нормальных трещин выполняем из условия:
аcr = ss·y/Es £ 0,02 см; (2.30)
где аcr – величина раскрытия трещины;
ss – напряжения в арматуре;
ss = n·Mтр·(hо – x)/Ired; (2.31)
y – коэффициент раскрытия трещин для стержневой арматуры периодического профиля;
0,02 см – допустимая величина раскрытия трещин;
y= ![]() ;
(2.32)
;
(2.32)
Rr – радиус взаимодействия бетона с арматурой:
Rr = Аr/(åb·n·do); (2.33)
Аr – площадь зоны взаимодействия для нормального сечения;
Аr = b·(do /2 + 2см + 6·do); (2.34)
b = 1 - коэффициент зависящий от расстановки арматуры для одиночных стержней;
n = 11 – число арматурных стержней;
dо = 12 мм – диаметр арматуры.
ss = 5,72·29·103·(0,244 – 0,0522)/3,0918·10-4 = 103 МПа;
Аr = 100·(1,2/2 + 2см + 6·1,2) = 980 см2;
Rr = 980/(1·11·1,2) = 74,24 см;
y = ![]() ;
;
аcr = 103·12,92/206000 £ 0,02 см;
0,013 < 0,02 см - Условие выполняется.
В результате проведённых проверок принимаем 11 стержней арматуры класса AI и диаметром 12 мм.
После выполнения ручного расчёта производим компьютерную проверку, результаты которой представлены в приложении 1.
2.6 Расчет главной балки пролетного строения
Для расчета принимаем разрезную балку из обычного железобетона с расчетным пролетом lp = 26,9 м. Расчет главной балки производим на прочность, выносливость и трещиностойкость.
2.6.1 Построение линий влияния внутренних усилий в главной балке
Необходимые для расчетов
линии влияния усилий в главной балке изображены на рисунке 2.3. Необходимо
помнить, что при устройстве пути на балласте эквивалентные нагрузки во всех
формулах определяем при ![]() , независимо от
положения вершин линий влияния и при выполнении ограничения
, независимо от
положения вершин линий влияния и при выполнении ограничения ![]() , кН/м.
, кН/м.
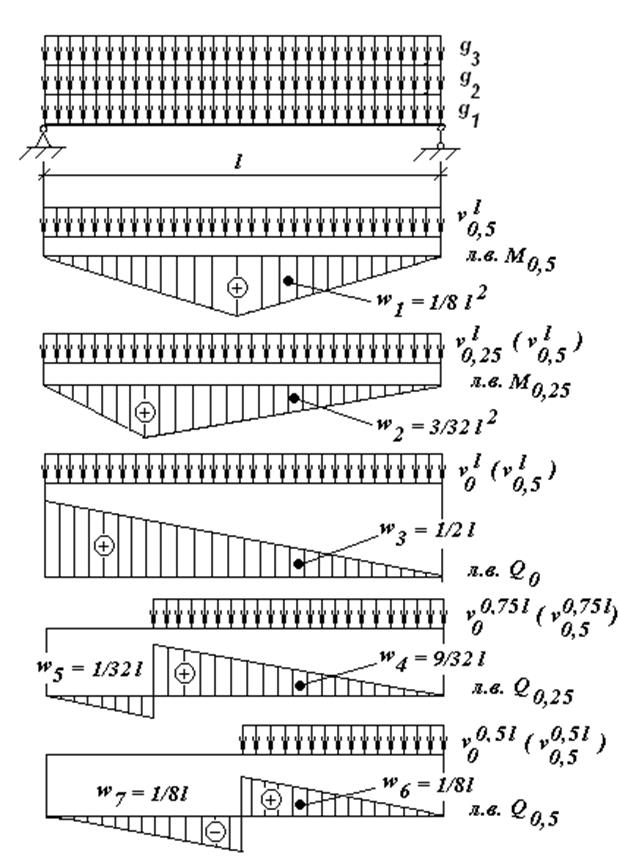
Рисунок 2.3 - Линии влияния внутренних усилий в главной балке
Вычислим необходимые для дальнейших расчетов площади линий влияния:
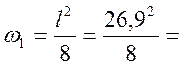 90,45 м2;
90,45 м2;
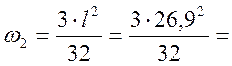 67,84 м2;
67,84 м2;
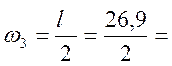 13,45 м2;
13,45 м2;
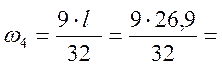 7,57 м2;
7,57 м2;
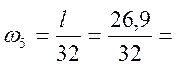 0,84 м2;
0,84 м2;
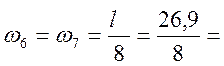 3,36 м2.
3,36 м2.
2.6.2 Определение нагрузок
Все нагрузки: постоянные и временные считаем равномерно распределенными по всей длине моста.
Постоянные нагрузки:
- нагрузку от собственного веса определяем по формуле:
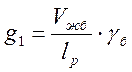 ,
,![]() (2.35)
(2.35)
где ![]() - объем железобетона пролетного
строения, который определяем в зависимости от расчетной длины пролетного
строения [2, П.1.1],
- объем железобетона пролетного
строения, который определяем в зависимости от расчетной длины пролетного
строения [2, П.1.1], ![]() = 83 м
= 83 м![]() ;
; ![]() -
удельный вес бетона,
-
удельный вес бетона, ![]() =24,5 кH/м
=24,5 кH/м![]() ;
; ![]() -
расчетная длина пролетного строения
-
расчетная длина пролетного строения ![]() = 26,9 м.
= 26,9 м.
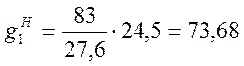 кН/м;
кН/м;
![]() кН/м.
кН/м.
- нагрузка от балласта с частями пути:
![]() кН/м;
кН/м;
![]() кН/м
кН/м
-
нагрузка от тротуаров с перилами: ![]() = 9,8 кН/м;
= 9,8 кН/м;
![]() кН/м.
кН/м.
![]() кН/м;
кН/м; ![]() кН/м.
кН/м.
Временные
нагрузки: определяем от подвижного состава при ![]() с
помощью интерполяции:
с
помощью интерполяции:
![]() кН/м;
кН/м;
![]() кН/м;
кН/м;
![]() кН/м;
кН/м;
2.6.3 Определение расчетных усилий
Определение коэффициентов для нагрузок:
-
коэффициенты надежности по постоянным нагрузкам определяем в соответствии с
п.2.10 [1]: ![]()
![]()
![]() 1,1 и
1,1 и ![]() =1,3;
=1,3;
-
коэффициенты надежности по временным нагрузкам определяем в соответствии с
п.2.23 [1] по интерполяции в зависимости от величины загружения ![]() :
:
![]() ;
; ![]() ;
; ![]() .
.
-
динамические коэффициенты определяем в соответствии с п.2.22 [1] в зависимости
от длины загружения ![]() :
:
![]() 26,9;
26,9; 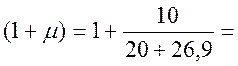 1,21;
1,21;
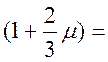 1,14;
1,14;
![]() 0,86 – коэффициент, учитывающий
наличие в поездах только перспективных локомотивов и вагонов, а также
отсутствие тяжелых транспортеров; определен для
0,86 – коэффициент, учитывающий
наличие в поездах только перспективных локомотивов и вагонов, а также
отсутствие тяжелых транспортеров; определен для ![]() 26,9
в соответствии с п.2.11 [1].
26,9
в соответствии с п.2.11 [1].
1) Усилия для расчетов на прочность:
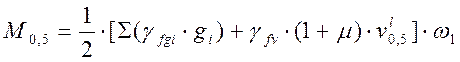 , (2.36)
, (2.36)
где ![]() ,
, ![]() -
коэффициенты надежности по постоянным и временным нагрузкам;
-
коэффициенты надежности по постоянным и временным нагрузкам;
![]() - площадь линии влияния для
- площадь линии влияния для ![]() ,
, ![]() =
90,45 м
=
90,45 м![]() .
.
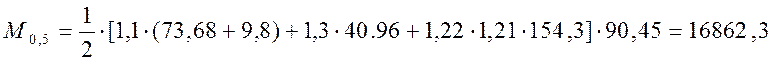 кНм.
кНм.
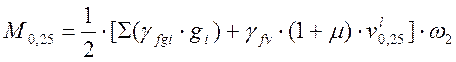 , (2.37)
, (2.37)
где ![]() - площадь линии влияния для
- площадь линии влияния для ![]() ,
, ![]() =
67,84 м2.
=
67,84 м2.
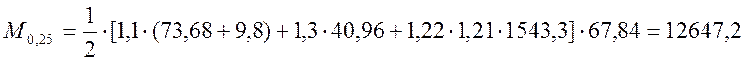 кН/м.
кН/м.
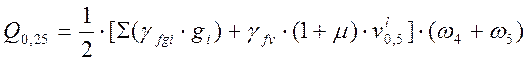 , (2.38)
, (2.38)
где ![]() ,
, ![]() -
площади линии влияния для
-
площади линии влияния для ![]() , равные 7,57 м
, равные 7,57 м![]() и (-0,84 м
и (-0,84 м![]() ) соответственно.
) соответственно.
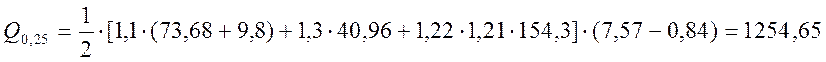 кН.
кН.
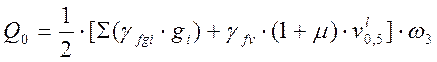 , (2.39)
, (2.39)
где ![]() - площадь линии влияния для
- площадь линии влияния для ![]() ,
, ![]() =
13,45 м
=
13,45 м![]() .
.
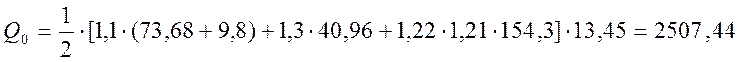 кН.
кН.
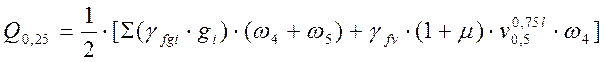 , (2.40)
, (2.40)
где ![]() - коэффициент надежности по
временной нагрузке для
- коэффициент надежности по
временной нагрузке для ![]() ,
, ![]() =
1,24;
=
1,24;
![]() - динамический коэффициент для
- динамический коэффициент для ![]() ,
, ![]() =
1,25;
=
1,25;
![]() - нагрузка от подвижного состава для
- нагрузка от подвижного состава для
![]() ,
,
![]() = 165,46 кH/м.
= 165,46 кH/м.
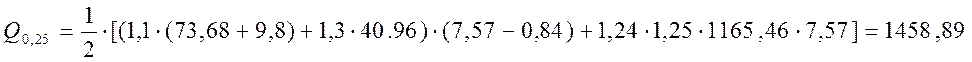 кН
кН
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.