Определение размеров выборки в результате проведенных наблюдений за шарнирными элементами тормозной рычажной передачи пассажирского вагона (Глава дипломного проекта), страница 6

К	Границы интервалов	Абсолютная частота hm	Нормированные середины интервалов	Ф(zm)	Вероятность
1	0,01-0,07	3	- 0,725	0,3079	0,044
2	0,07-0,13	8	- 0,112	0,3965	0,0886
3	0,13-0,19	4	0,5	0,3521	0,1366
4	0,19-0,25	1	1,11	0,2155	0,3079
Σ	-	16	-	-	-

Наблюдаемое значение критерия x²_набл определяем по таблице

 

Расчет теоретических частот и критерия x²                                        Таблица

К	Абсолютная частота hm	Вероятность
1	3	0,044	4,926	1,926	3,711
2	8	0,0886	1,417	6,58	37,32
3	4	0,1366	0,704	3,296	10,86
4	1	0,3079	2,18	1,185	1,406
Σ	16	-	-	-	-

Рис 4.15. Теоретическая кривая распределения величины износа

 

Определение теоретической вероятности распределения                 Таблица

К	Середина интервала xm	Абсолютная частота hm	Нормированные середины интервалов	Плотность вероятности	Вероятность
1	0,0275	1	- 1, 92	0,0632	0,034
2	0,0625	7	- 0,69	0,3144	0,16
3	0,0975	6	0, 542	0,3448	0,175
4	0,1325	2	1,77	0,0833	0,06
Σ	-	16	-	-	-

Вероятность Р собой разность соответствующих значений интегралов вероятности:

;

где Ф(z) – интеграл вероятности выбираем по

Определение теоретической вероятности распределения                            Таблица

К	Границы интервалов	Абсолютная частота hm	Нормированные середины интервалов	Ф(zm)	Вероятность
1	0,01-0,045	1	- 1, 72	0,0909	0,0909
2	0,045-0,08	7	- 0,49	0,3538	0,2227
3	0.08-0,115	6	0, 342	0,3765	0,2602
4	0,115-0,15	2	1,57	0,1163	0,2629
Σ	-	16	-	-	-

Наблюдаемое значение критерия x²_набл определяем по таблице

 

Расчет теоретических частот и критерия x²                                        Таблица

К	Абсолютная частота hm	Вероятность
1	1	0,0909	1,454	0,454	0,206
2	7	0,2227	4,2	2,79	7,8
3	6	0,2602	0,3632	5,63	30,77
4	2	0,2629	4,02	2,02	4,08
Σ	16	-	-	-	-

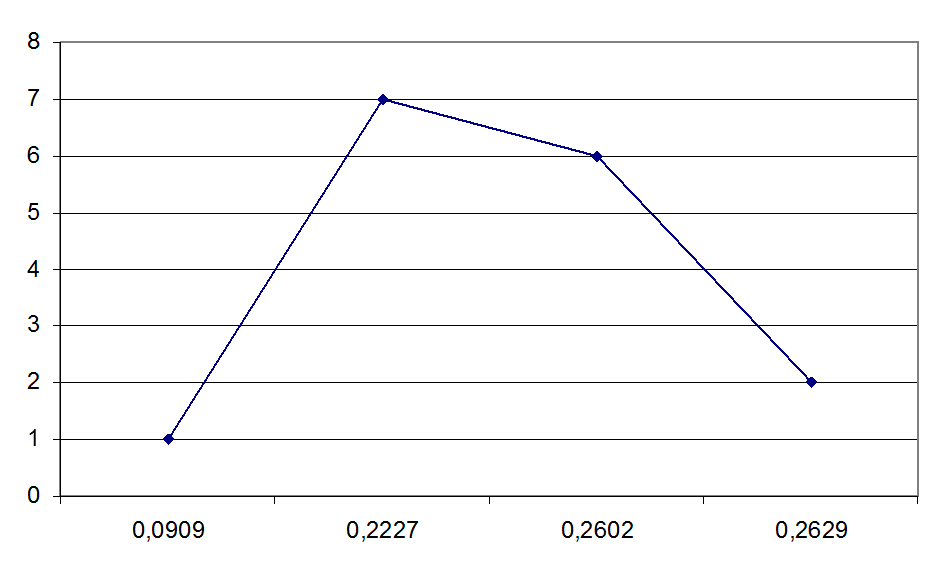Рис 4.16. Теоретическая кривая распределения величины износа

 

4.8.  Статистическая оценка надежности элементов тормозной рычажной передачи в процессе эксплуатации

          Для оценки надежности вагонов и их элементов используют количественные характеристики надежности, которые можно определить по представленным статистическим данным об отказах, полученным в процессе эксплуатации или в результате специальных опытов, поставленных с учетом особенностей работы изделия и наличия или отсутствия ремонта.

Исходные данные                                                                        Таблица

№ п/п	Наименование узла ТРП	Количество втулок, N	Количество отказов, n	Среднегодовой пробег, Lтыс.км.	Удельный износ, мм/105км
					втулки	валики
1	Тормозной башмак	32	4	250	0,1328	0,1179
2	Нижняя подвеска	32	3	250	0,1102	0,0677

          4.9. Определение вероятности безотказной работы при постепенных отказах

1.  Согласно руководству по деповскому ремонту пассажирских вагонов зазор e в шарнире тормозной рычажной передачи не должен превышать 3 мм.

2.  Срок службы (средний пробег) безотказной работы (по износу) предлагаемых пар трения:

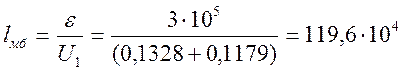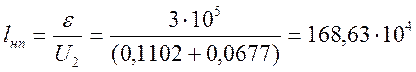 км;

 км.

3.  Величина средней выборочной продолжительности безотказной работы (по износу):

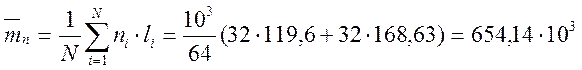км

4.  Среднее квадратичное отклонение:

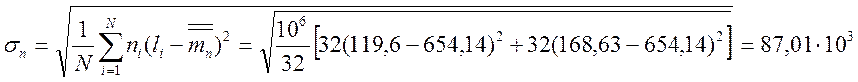 км

5.  Нижняя доверительная граница средней статистической продолжительности безотказной работы по предельному износу при принятой величине достоверности

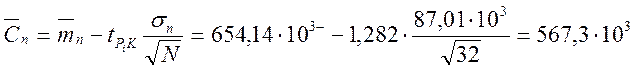 км

6.  Задаваясь значением пробегов 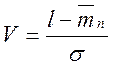, находим величину Р_n(l), выраженную нормальной функцией распределения.

4.10. Определение вероятности безотказной работы при внезапных отказах

1.  Средняя выборочная продолжительность безотказной работы

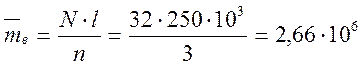 км

2.  Интенсивность отказов

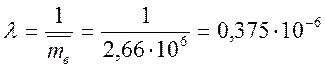 1/км

3.  Нижняя доверительная граница средней статистической продолжительности безотказной работы  при принятой величине доверительности Р=0,90:

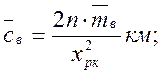
где К = 2n + 2 = 2 × 10 + 2  = 22;

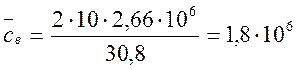 км

4.  Вероятность безотказной работы при внезапных отказах