Определение размеров выборки в результате проведенных наблюдений за шарнирными элементами тормозной рычажной передачи пассажирского вагона (Глава дипломного проекта), страница 5

К	Середина интервала x_m	Абсолютная частота h_m	Нормированные середины интервалов	Плотность вероятности	Вероятность
1	0,10875	3	- 1,437	0,1415	0,0707
2	0,12625	6	- 0,391	0,3697	0,185
3	0,14375	5	0,654	0,323	0,161
4	0,16125	2	1,7	0,094	0,452
Σ	-	16	-	-	-

Вероятность Р собой разность соответствующих значений интегралов вероятности:

;

где Ф(z) – интеграл вероятности выбираем по

Определение теоретической вероятности распределения Таблица

К	Границы интервалов	Абсолютная частота h_m	Нормированные середины интервалов	Ф(z_m)	Вероятность
1	0,1-0,1175	3	- 1,437	0,1435	0,1435
2	0,1175-0,135	6	- 0,391	0,3697	0,22
3	0,135-0,1525	5	0,654	0,3230	0,2262
4	0,1527-0,17	2	1,7	0,094	0,229
Σ	-	16	-	-	-

Наблюдаемое значение критерия x²_набл определяем по таблице

Расчет теоретических частот и критерия x² Таблица

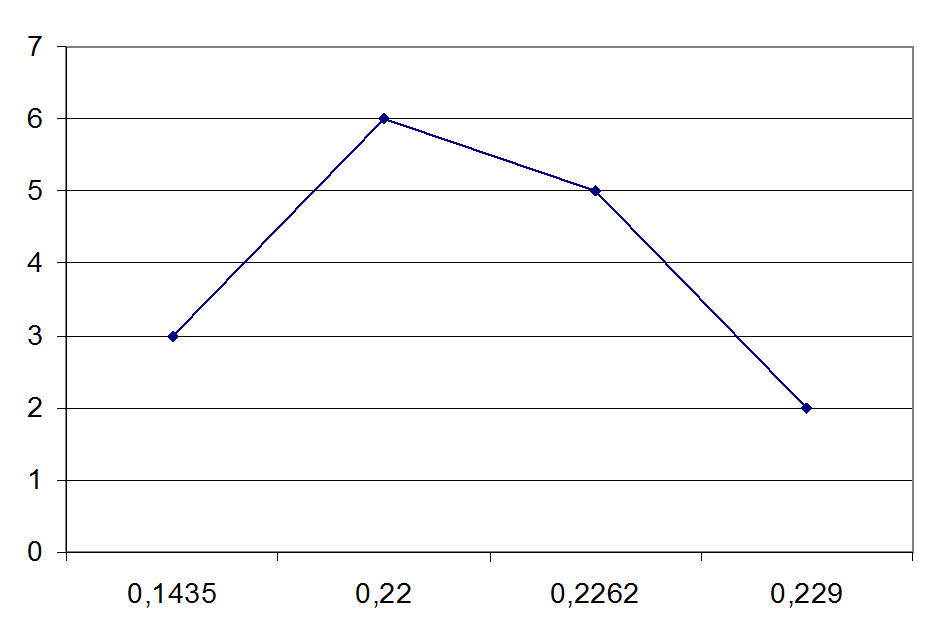
Рис 4.13. Теоретическая кривая распределения величины износа

Определение теоретической вероятности распределения Таблица

К	Середина интервала x_m	Абсолютная частота h_m	Нормированные середины интервалов	Плотность вероятности	Вероятность
1	0,06875	4	- 1,133	0,2107	0,1053
2	0,10625	5	- 0,2836	0,3836	0,192
3	0,14375	5	0,705	0,3123	0,156
4	0,18125	2	1,695	0,0957	0,05
Σ	-	16	-	-	-

Вероятность Р собой разность соответствующих значений интегралов вероятности:

;

где Ф(z) – интеграл вероятности выбираем по

Определение теоретической вероятности распределения Таблица

К	Границы интервалов	Абсолютная частота h_m	Нормированные середины интервалов	Ф(z_m)	Вероятность
1	0,05-0,0875	4	- 1,133	0,2107	0,0713
2	0,0875-0,125	5	- 0,2836	0,3836	0,1729
3	0,125-0,1625	5	0,705	0,3123	0,2107
4	0,1625-0,2	2	1,695	0,0957	0,2166
Σ	-	16	-	-	-

Наблюдаемое значение критерия x²_набл определяем по таблице

Расчет теоретических частот и критерия x² Таблица

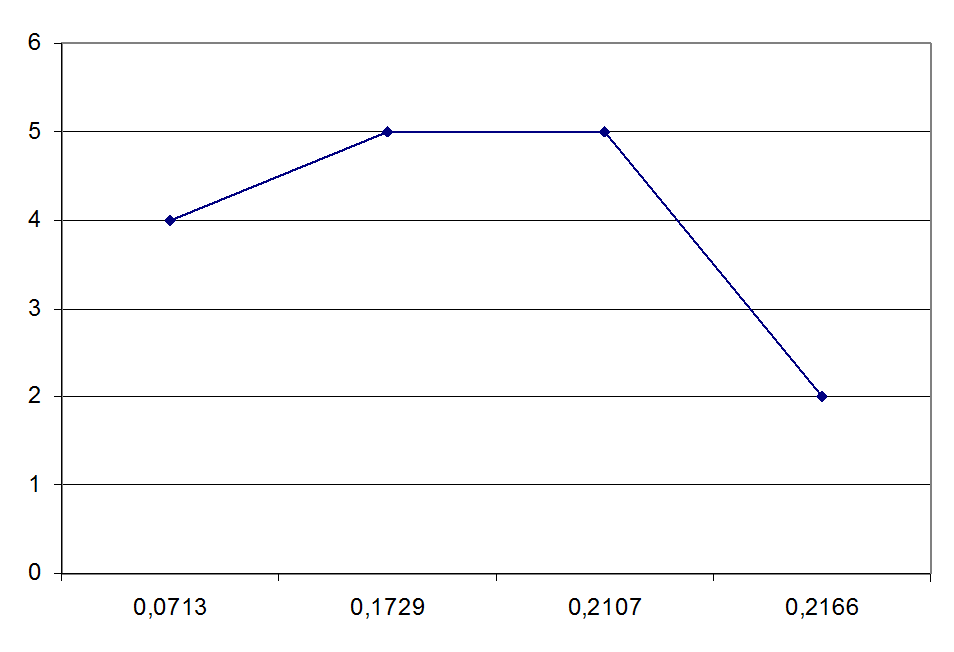
Рис 4.14. Теоретическая кривая распределения величины износа

Определение теоретической вероятности распределения Таблица

К	Середина интервала x_m	Абсолютная частота h_m	Нормированные середины интервалов	Плотность вероятности	Вероятность
1	0,04	3	- 0,725	0,3079	0,155
2	0,1	8	- 0,112	0,3965	0,12
3	0,16	4	0,5	0,3521	0,176
4	0,22	1	1,11	0,2155	0,107
Σ	-	16	-	-	-

Вероятность Р собой разность соответствующих значений интегралов вероятности:

;

где Ф(z) – интеграл вероятности выбираем по

Определение теоретической вероятности распределения Таблица

1 2 3 4 5 6

К