В качестве числовых характеристик одного измеряемого параметра случайной величины принимаем среднеарифметическое; среднее квадратичное отклонение – S; дисперсию S и коэффициент вариации V.
Вычисление среднего арифметического производим по формуле:
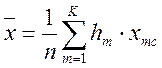 ;
;
где hm – абсолютная частота m – го интервала;
xmc – соответствующая середина интервала;
К – число интервалов;
n – число измерений.
В практике статистических исследований в качестве меры рассеивания используется среднее квадратичное отклонение S, а его квадрат называется дисперсией.
Эмпирическая дисперсия определяем по следующей формуле:
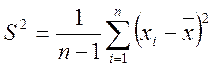
Как и в предыдущем разделе сначала определим числовые характеристики величины износа втулки верхней подвески башмака, используя данные из табл. Для удобства вычисления составим следующую таблицу:
Определение числовых характеристик Таблица
К |
Границы интервалов |
Середина интервалов xm |
Абсолютная частота hm |
xm× hm |
|
|
|
|
1 |
0,1 – 0,1175 |
0,10875 |
3 |
0,32625 |
- 0,02405 |
0,000578 |
0,00173 |
|
2 |
0,1175 – 0,135 |
0,12625 |
6 |
0,7575 |
- 0,00655 |
0,000043 |
0,000258 |
|
3 |
0,135 – 0,1525 |
0,14375 |
5 |
0,71875 |
0,01095 |
0,00012 |
0,0006 |
|
4 |
0,1525 – 0,17 |
0,16125 |
2 |
0,3225 |
0,02845 |
0,000809 |
0,00162 |
|
S |
- |
- |
16 |
2,125 |
- |
- |
0,0042 |
Определяем среднее арифметическое значение величины износа:
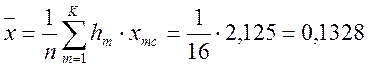 мм
мм
Определяем дисперсию и среднее квадратичное отклонение величины износа:
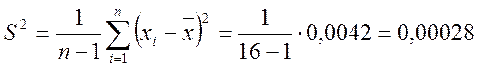 мм
мм
![]() мм
мм
Проверку ![]() и S выполним
упрощенным способом – способом введения вспомогательного
и S выполним
упрощенным способом – способом введения вспомогательного ![]() :
:
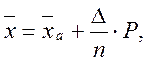 мм
мм
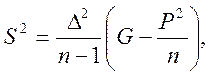 мм
мм
Среднее значение ряда определяем по следующей формуле:
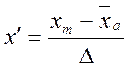 ,
,
где Δ = 0,0175 - величины интервала группирования
Последовательность расчета сводим в таблицу
Расчет среднего
арифметического ![]() и S2 по таблице частот Таблица
и S2 по таблице частот Таблица
К |
Границы интервалов |
Середина интервалов xm |
Абсолютная частота hm |
Середина условного интервала x́m |
x́m× hm |
|
|
1 |
0,1 – 0,1175 |
0,10875 |
3 |
- 1,5 |
- 4,5 |
6,75 |
|
2 |
0,1175 – 0,135 |
0,12625 |
6 |
- 0,5 |
- 3 |
1,5 |
|
3 |
0,135 – 0,1525 |
0,14375 |
5 |
0,5 |
2,5 |
1,25 |
|
4 |
0,1525 – 0,17 |
0,16125 |
2 |
1,5 |
3 |
4,5 |
|
Σ |
- |
- |
16 |
- |
Р = - 2 |
G = 14 |
Значение ![]() выбираем по наибольшей частоте,
выбираем по наибольшей частоте, ![]() = 0,135 мм:
= 0,135 мм:
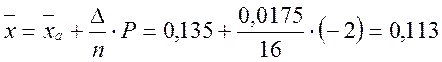 мм;
мм;
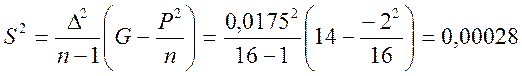 мм;
мм;
![]()
Два способа дали одинаковые
результаты, значит значения ![]() и S
найдены верно.
и S
найдены верно.
Определим коэффициент вариации:
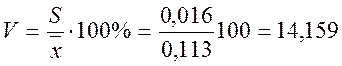 %
%
Аналогичным способом определим числовые характеристики для величины износа остальных элементов подвески тормозного башмака.
Составим таблицы для определения числовых характеристик, используя данные из таблиц
Определение числовых характеристик Таблица
К |
Границы интервалов |
Середина интервалов xm |
Абсолютная частота hm |
xm× hm |
|
|
|
|
1 |
0,05 – 0,0875 |
0,06875 |
4 |
0,275 |
- 0,04915 |
0,002415 |
0,00966 |
|
2 |
0,0875 – 0,125 |
0,10625 |
5 |
0,53125 |
- 0,01165 |
0,0001357 |
0,000678 |
|
3 |
0,125 – 0,1625 |
0,14375 |
5 |
0,71875 |
0,02585 |
0,00066 |
0,0033 |
|
4 |
0,1625 – 0,2 |
0,18125 |
2 |
0,3625 |
0,06335 |
0,004013 |
0,00802 |
|
S |
- |
- |
16 |
1,8875 |
- |
- |
0,02165 |
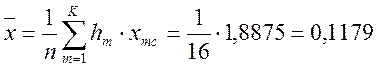 мм
мм
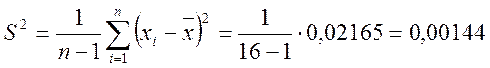 мм
мм
![]() мм
мм
Проверку ![]() и S выполним
упрощенным способом – способом введения вспомогательного
и S выполним
упрощенным способом – способом введения вспомогательного ![]() :
:
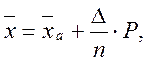 мм
мм
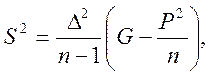 мм
мм
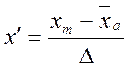 ,
,
Δ = 0,0375 - величины интервала группирования
Расчет среднего
арифметического ![]() и S2 по таблице частот Таблица
и S2 по таблице частот Таблица
К |
Границы интервалов |
Середина интервалов xm |
Абсолютная частота hm |
Середина условного интервала x́m |
x́m× hm |
|
|
1 |
0,05 – 0,0875 |
0,06875 |
4 |
- 1,5 |
- 6 |
9 |
|
2 |
0,0875 – 0,125 |
0,10625 |
5 |
- 0,5 |
- 2,5 |
1,25 |
|
3 |
0,125 – 0,1625 |
0,14375 |
5 |
0,5 |
2,5 |
1,25 |
|
4 |
0,1625 – 0,2 |
0,18125 |
2 |
1,5 |
3 |
4,5 |
|
Σ |
- |
- |
16 |
- |
Р = - 3 |
G = 16 |
Значение ![]() выбираем по наибольшей частоте,
выбираем по наибольшей частоте, ![]() = 0,125 мм:
= 0,125 мм:
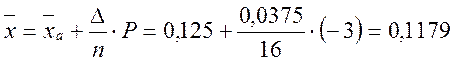 мм;
мм;
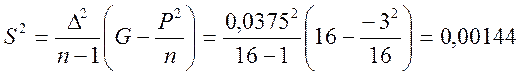 мм;
мм;
![]()
Два способа дали одинаковые
результаты, значит значения ![]() и S
найдены верно.
и S
найдены верно.
Определим коэффициент вариации:
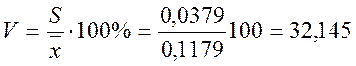 %
%
Определение числовых характеристик Таблица
К |
Границы интервалов |
Середина интервалов xm |
Абсолютная частота hm |
xm× hm |
|
|
|
|
1 |
0,01 – 0,07 |
0,04 |
3 |
0,12 |
- 0,0712 |
0,00507 |
0,0152 |
|
2 |
0,07 – 0,13 |
0,1 |
8 |
0,8 |
- 0,0112 |
0,000125 |
0,001 |
|
3 |
0,13 – 0,19 |
0,16 |
4 |
0,64 |
0,0488 |
0,00238 |
0,00952 |
|
4 |
0,19 – 0,25 |
0,22 |
1 |
0,22 |
0,1088 |
0,1183 |
0,1183 |
|
S |
- |
- |
16 |
1,78 |
- |
- |
0,144 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.