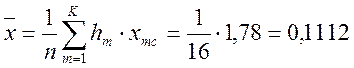 мм
мм
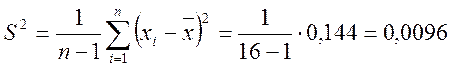 мм
мм
![]() мм
мм
Проверку ![]() и S выполним
упрощенным способом – способом введения вспомогательного
и S выполним
упрощенным способом – способом введения вспомогательного ![]() :
:
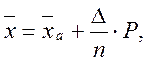 мм
мм
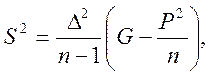 мм
мм
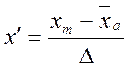 ,
,
Δ = 0,06 - величины интервала группирования
Расчет среднего
арифметического ![]() и S2 по таблице частот Таблица
и S2 по таблице частот Таблица
К |
Границы интервалов |
Середина интервалов xm |
Абсолютная частота hm |
Середина условного интервала x́m |
x́m× hm |
|
|
1 |
0,01 – 0,07 |
0,04 |
3 |
- 1,5 |
- 4,5 |
6,75 |
|
2 |
0,07 – 0,13 |
0,1 |
8 |
- 0,5 |
-4 |
2 |
|
3 |
0,13 – 0,19 |
0,16 |
4 |
0,5 |
2 |
1 |
|
4 |
0,19 – 0,25 |
0,22 |
1 |
1,5 |
1,5 |
2,25 |
|
Σ |
- |
- |
16 |
- |
Р = - 5 |
G = 12 |
Значение ![]() выбираем по наибольшей частоте,
выбираем по наибольшей частоте, ![]() = 0,13 мм:
= 0,13 мм:
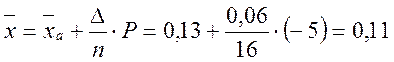 мм;
мм;
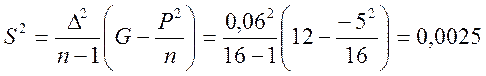 мм;
мм;
![]()
Два способа дали одинаковые
результаты, значит значения ![]() и S
найдены верно.
и S
найдены верно.
Определим коэффициент вариации:
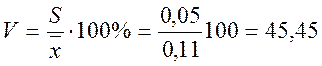 %
%
Определение числовых характеристик Таблица
К |
Границы интервалов |
Середина интервалов xm |
Абсолютная частота hm |
xm× hm |
|
|
|
|
1 |
0,01 – 0,045 |
0,0275 |
1 |
0,0275 |
- 0,0546 |
0,00298 |
0,00298 |
|
2 |
0,045 – 0,08 |
0,0625 |
7 |
0,4375 |
- 0,0196 |
0,000384 |
0,00268 |
|
3 |
0,08 – 0,115 |
0,0975 |
6 |
0,585 |
0,0154 |
0,000237 |
0,00142 |
|
4 |
0,115 – 0,15 |
0,1325 |
2 |
0,265 |
0,0504 |
0,00254 |
0,00508 |
|
S |
- |
- |
16 |
1,315 |
- |
- |
0,01216 |
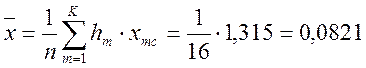 мм
мм
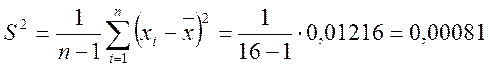 мм
мм
![]() мм
мм
Проверку ![]() и S выполним
упрощенным способом – способом введения вспомогательного
и S выполним
упрощенным способом – способом введения вспомогательного ![]() :
:
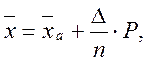 мм
мм
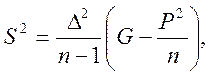 мм
мм
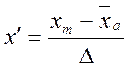 ,
,
Δ = 0,035 - величины интервала группирования
Расчет среднего
арифметического ![]() и S2 по таблице частот Таблица
и S2 по таблице частот Таблица
К |
Границы интервалов |
Середина интервалов xm |
Абсолютная частота hm |
Середина условного интервала x́m |
x́m× hm |
|
|
1 |
0,01 – 0,045 |
0,0275 |
1 |
- 1,5 |
- 1,5 |
2,25 |
|
2 |
0,045 – 0,08 |
0,0625 |
7 |
- 0,5 |
- 3,5 |
1,75 |
|
3 |
0,08 – 0,115 |
0,0975 |
6 |
0,5 |
3 |
1,5 |
|
4 |
0,115 – 0,15 |
0,1325 |
2 |
1,5 |
3 |
5 |
|
Σ |
- |
- |
16 |
- |
Р = 1 |
G = 10,5 |
Значение ![]() выбираем по наибольшей частоте,
выбираем по наибольшей частоте, ![]() = 0,08 мм:
= 0,08 мм:
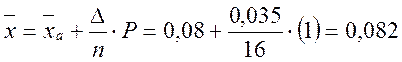 мм;
мм;
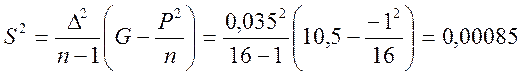 мм;
мм;
![]()
Два способа дали одинаковые
результаты, значит значения ![]() и S
найдены верно.
и S
найдены верно.
Определим коэффициент вариации:
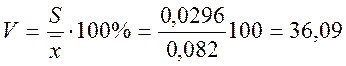 %
%
4.7. Проверка гипотез о соответствии распределения величины износа теоретическому закону распределения.
Статистическая проверка гипотез применяется для того, чтобы использовать полученную по выборке информацию для суждения о законе распределения генеральной совокупности. При этом имеется определенное представление о неизвестном вероятном законе F(x) и его параметрах, которые формируются в виде статистической основной Hили нулевой H0 гипотез.
Принимаем для генеральной
совокупности: m(x)
x= ![]() и σ = S,
и σ = S,
где m(x), σ - соответственно математическое ожидание и среднее квадратичное отклонение для генеральной совокупности.
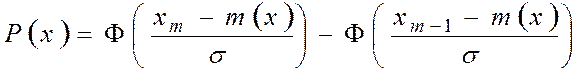
где Р(x) - вероятность попадания случайной величины в интервалах (xm-1,xm);
Ф(t) - интеграл вероятностей (табулированная функция).
Р(x) - можно определить также исходя из плотности распределения по средним значениям интервалов:
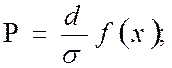
где f(x) - плотность распределения (табулированная функция).
Чтобы оценить вероятность гипотезы о соответствии данного распределения случайной величины теоретическому закону распределения, вводим так называемый уровень значимости, т.е. вероятность α настолько малую, что появление события с этой вероятностью следует считать практически невозможным.
Согласованность теоретического и эмпирического распределения можно проверить по критерию Пирсона:
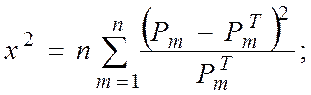
где Pm - наблюдаемое значение относительных частот;
PmT - теоретическая вероятность;
n - количество опытов.
По числу степеней свободы m и уровню значимости α, по таблице критических точек распределения c2 находим соответствующее ее значение и выполняем сравнение x2набл < x2набл
Проверяем гипотезу о соответствии распределения величин износа втулки верхней подвески тормозного башмака, используя данные из табл. Данные и последовательности расчета сводим в табл.
Определение теоретической вероятности распределения Таблица
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.