Определение размеров выборки в результате проведенных наблюдений за шарнирными элементами тормозной рычажной передачи пассажирского вагона (Глава дипломного проекта), страница 2

4.1. Группирование значений измеряемого параметра и его эмпирическое распределение

Проведем группирование опытных данных для данных из табл.    Затем определим наибольшее и наименьшее значение случайной величины и другие параметры:

X_max = 0,17

X_min = 0,1

Определим размах варьирования:

0,17-0,1 = 0,07

Определим величины интервала группирования:

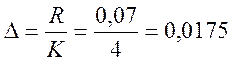
Составим вторичную таблицу или таблицу частот, где относительная частота равна:

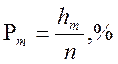
Таблица частот                                                                                       Таблица

К	Границы интервалов	Середина интервалов xm	Абсолютная частота hm	Относительная частота Рm, %	Накопленная частота Wн, %
1	0,1 – 0,1175	0,10875	3	0,1875	0,1875
2	0,1175 – 0,135	0,12625	6	0,375	0,5625
3	0,135 – 0,1525	0,14375	5	0,3125	0,8875
4	0,1525 – 0,17	0,16125	2	0,125	1
S	-	-	16	1	-

Для графического представления распределения частот строим гистограмму выборки. Для этого по оси абсцисс откладываем значения интервалов группирования случайной величины, а по оси ординат частоту для каждого интервала:

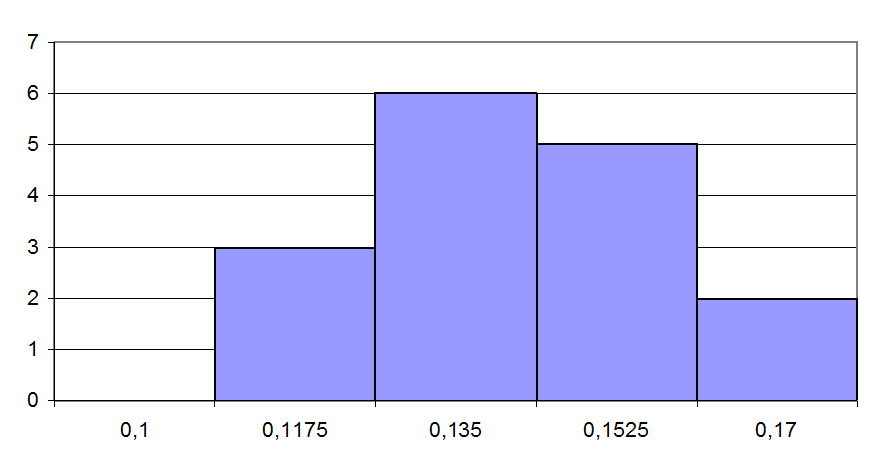
Рис 4.1 Гистограмма выборки

Соединив точки середин интервалов, получим полигон распределения значений случайной величины, соответствующей эмпирической кривой распределения:

 

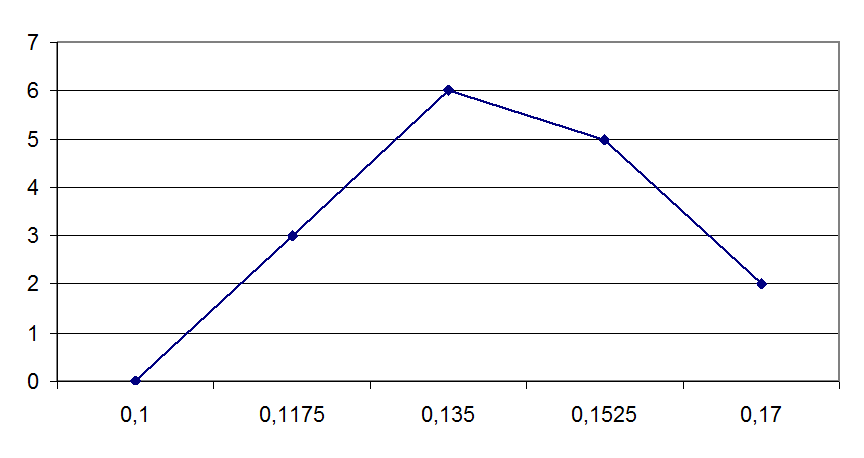Рис 4.2. Полигон частот

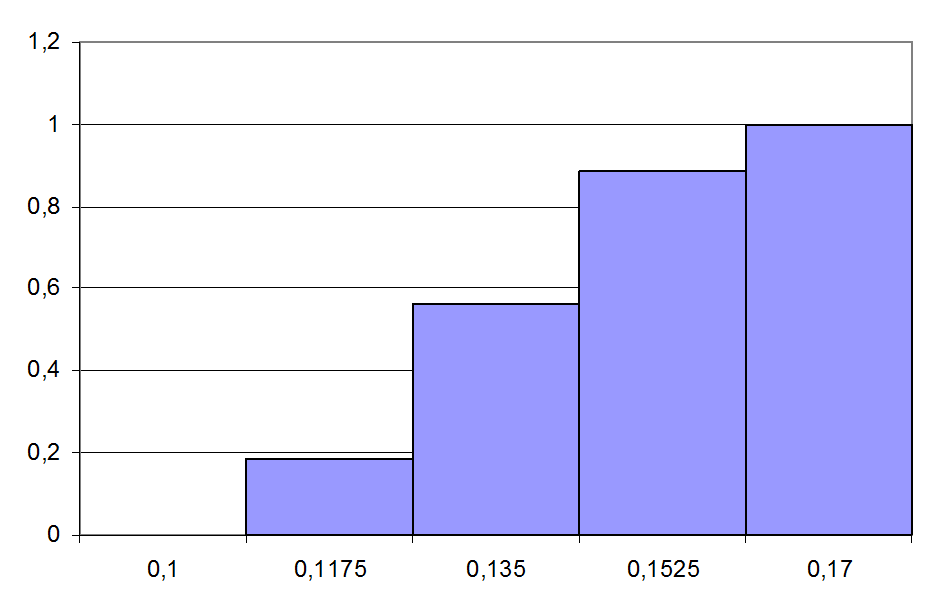
Рис 4.3.Ступенчатая кривая

Проведем группирование опытных данных для данных из табл.    Затем определим наибольшее и наименьшее значение случайной величины и другие параметры:

X_max = 0,2

X_min = 0,05

Определим размах варьирования:

0,2 - 0,05 = 0,15

Определим величины интервала группирования:

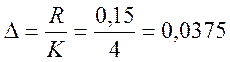
Составим вторичную таблицу или таблицу частот

Таблица частот                                                                                       Таблица

К	Границы интервалов	Середина интервалов xm	Абсолютная частота hm	Относительная частота Рm, %	Накопленная частота Wн, %
1	0,05 – 0,0875	0,06875	4	0,25	0,25
2	0,0875 – 0,125	0,10625	5	0,3125	0,5625
3	0,125 – 0,1625	0,14375	5	0,3125	0,8875
4	0,1625 – 0,2	0,18125	2	0,125	1
S	-	-	16	1	-

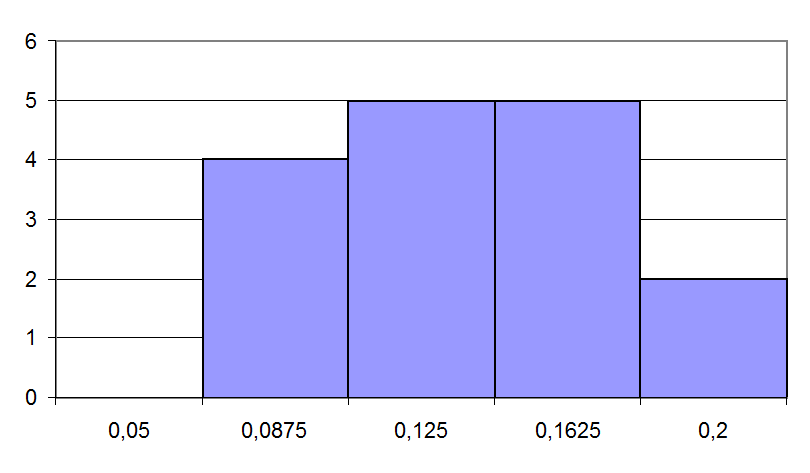
Рис 4.4. Гистограмма выборки

Соединив точки середин интервалов, получим полигон распределения значений случайной величины, соответствующей эмпирической кривой распределения:

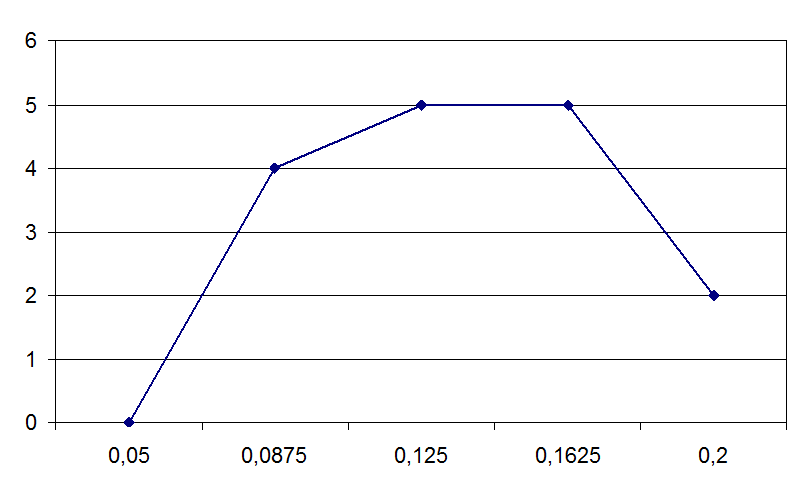
Рис 4.5. Полигон частот

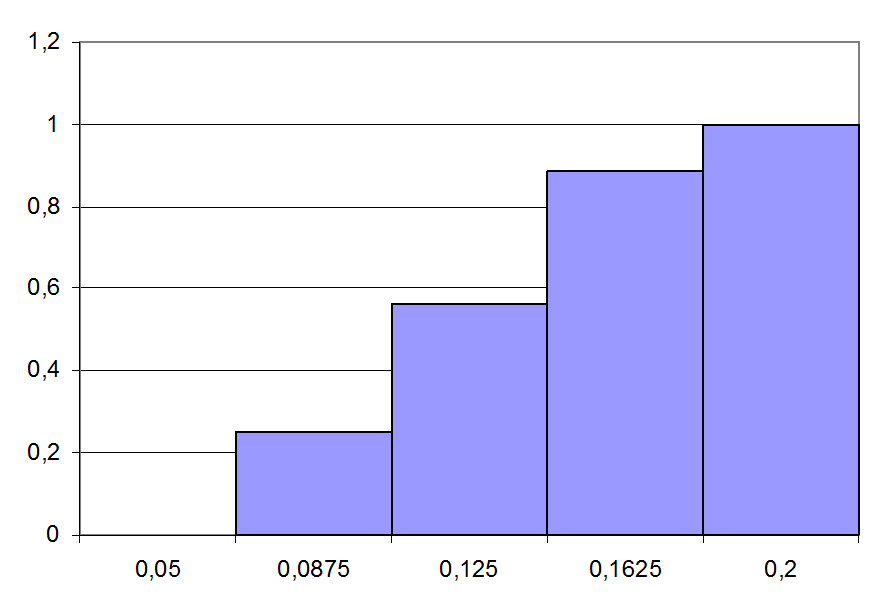
Рис 4.6.Ступенчатая кривая

Проведем группирование опытных данных для данных из табл.    Затем определим наибольшее и наименьшее значение случайной величины и другие параметры:

X_max = 0,25

X_min = 0,01

Определим размах варьирования:

0,25 - 0,01 = 0,24

Определим величины интервала группирования:

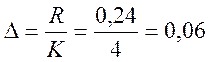
Составим вторичную таблицу или таблицу частот

Таблица частот                                                                                       Таблица

К	Границы интервалов	Середина интервалов xm	Абсолютная частота hm	Относительная частота Рm, %	Накопленная частота Wн, %
1	0,01 – 0,07	0,04	3	0,1875	0,1875
2	0,07 – 0,13	0,1	8	0,5	0,6875
3	0,13 – 0,19	0,16	4	0,25	0,9375
4	0,19 – 0,25	0,22	1	0,0625	1
S	-	-	16	1	-

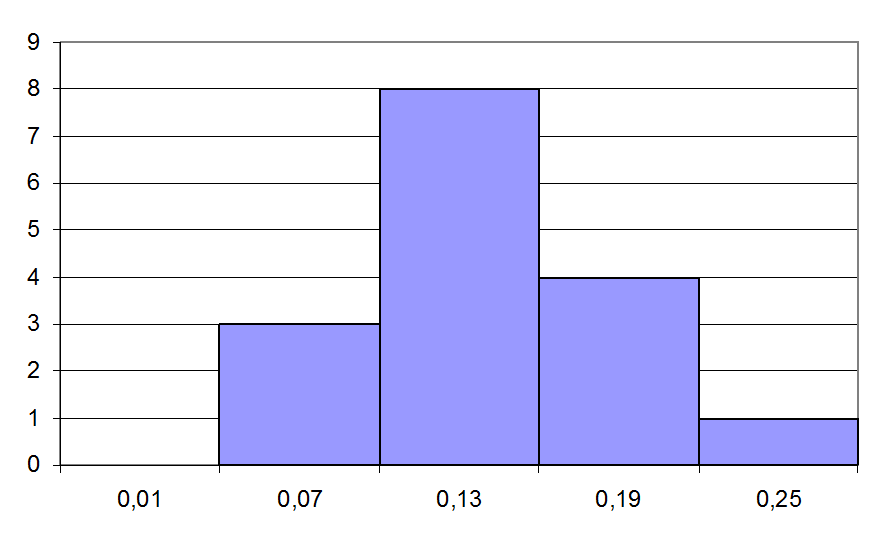
Рис 4.7  Гистограмма выборки

Соединив точки середин интервалов, получим полигон распределения значений случайной величины, соответствующей эмпирической кривой распределения:

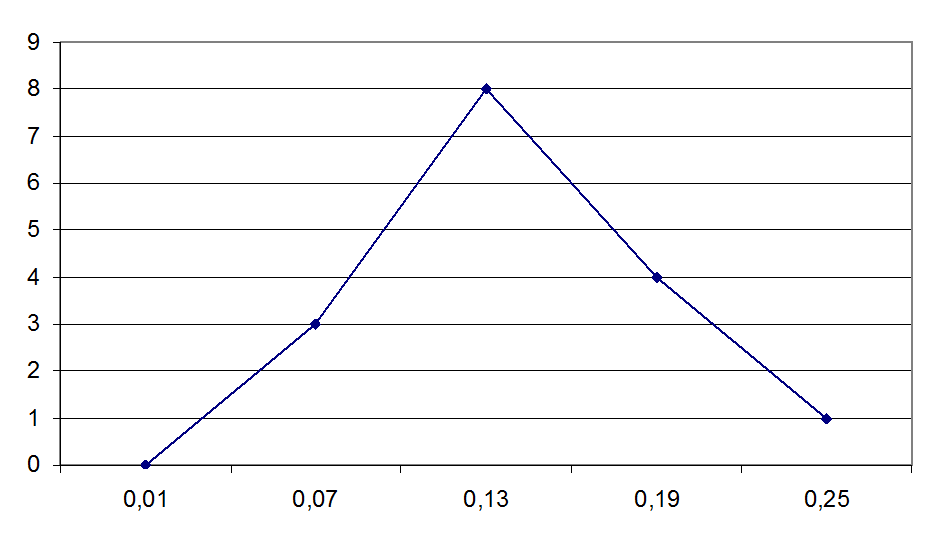
Рис 4.8. Полигон частот

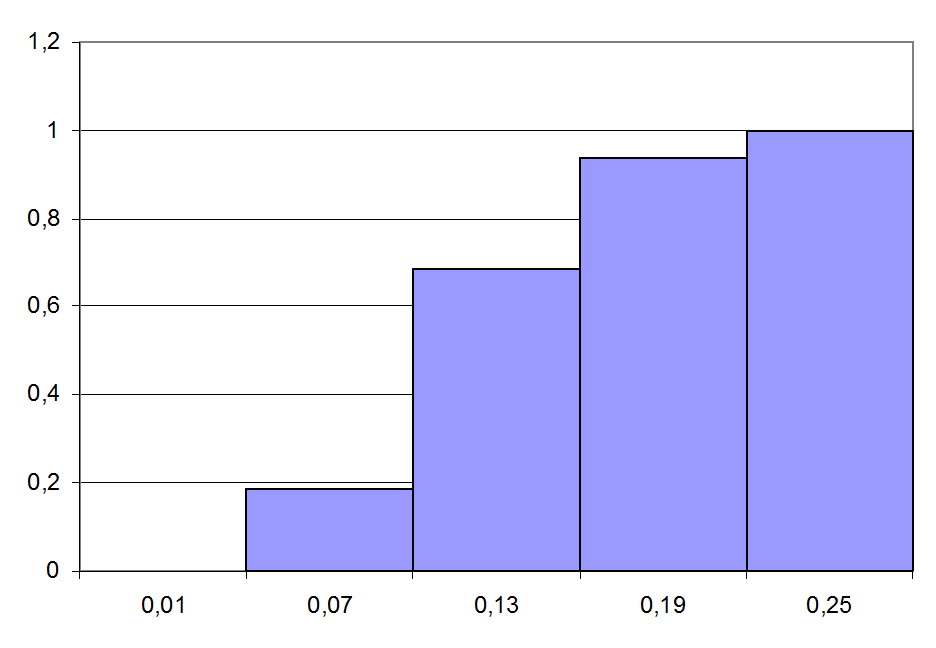
Рис 4.9. Ступенчатая кривая

Проведем группирование опытных данных для данных из табл.    Затем определим наибольшее и наименьшее значение случайной величины и другие параметры:

X_max = 0,15

X_min = 0,01

Определим размах варьирования:

0,15 - 0,01 = 0,14

Определим величины интервала группирования:

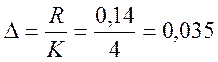
Составим вторичную таблицу или таблицу частот

Таблица частот                                                                                       Таблица

К	Границы интервалов	Середина интервалов xm	Абсолютная частота hm	Относительная частота Рm, %	Накопленная частота Wн, %
1	0,01 – 0,045	0,0275	1	0,0625	0,0625
2	0,045 – 0,08	0,0625	7	0,4375	0,5
3	0,08 – 0,115	0,0975	6	0,375	0,875
4	0,115 – 0,15	0,1325	2	0,3125	1
S	-	-	16	1	-

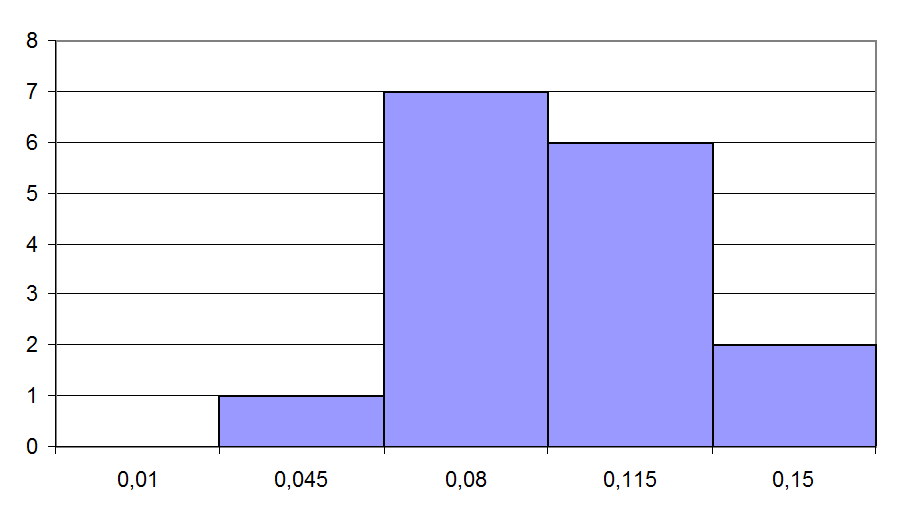
Рис 4.10.  Гистограмма выборки

Соединив точки середин интервалов, получим полигон распределения значений случайной величины, соответствующей эмпирической кривой распределения:

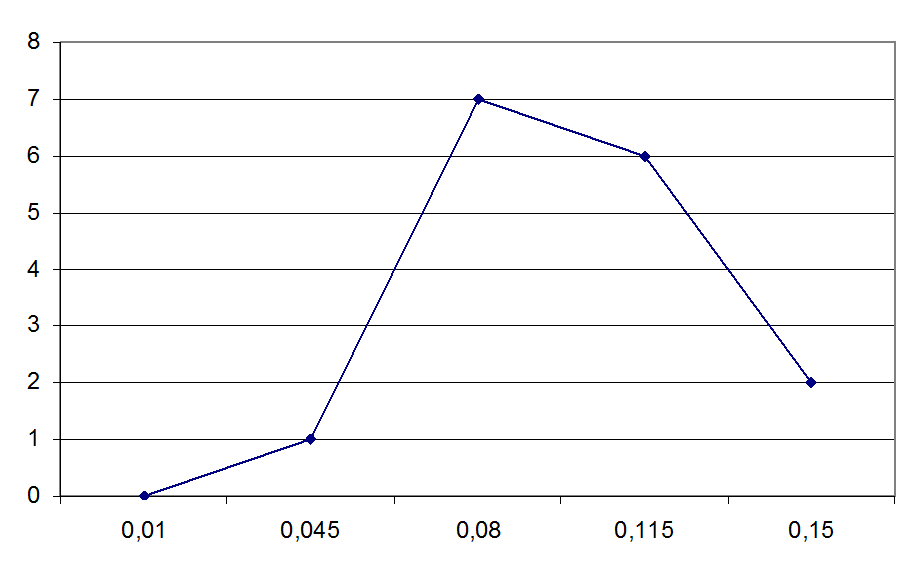
Рис 4.11. Полигон частот

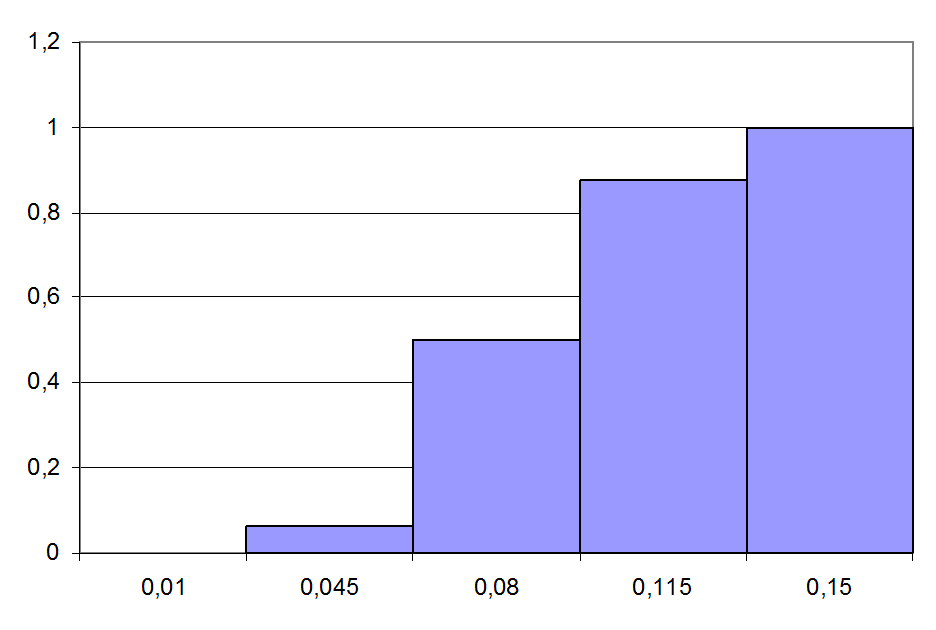
Рис 4.12. Ступенчатая кривая

 

4.6. Определение числовых характеристик измеряемого параметра