Эффективность автоматизации производственных процессов, страница 2

Задача оптимизации заключается в нахождении такого мно­жества А_rпри котором заданное количество всех видов продукции будет изготовлено наилучшим образом. Ее решение позволяет найти оптимальный уровень автоматизации производства, состав и параметры оборудования.

Оценку вариантов А_r(выбор оптимального варианта) произво­дят по критерию — удельные приведенные затраты на единицу продукции. В качестве условий и ограничений принимают: обеспе­чение выпуска заданного объема продукции; необходимость раз­мещения оборудования на производственной площади ограничен­ных размеров; обеспечение заданных показателей: число рабочих на участке, съем продукции с 1 м² производственной площади, удельный расход электроэнергии и др. В качестве ограничений могут выступать различные ресурсы (финансы, трудовые, энергия, сырье и материалы и др.), а также срок окупаемости и другие по­казатели.

Математическая модель оптимизации производства имеет вид:

где — капитальные затраты на r-вариант; Q— программа предприятия; — затраты на выпуск единицы продукции; ТЕ — срок окупаемости капитальных затрат; — годовой фонд рабо­чего времени; ,,,,— показатели по r-му варианту: производительность, производственная площадь, съем продукции с единицы производственной площади, энергоемкость, число лю­дей соответственно; ,,,— нормативные значения (или реальные характеристики производства): производственная пло­щадь, съем с единицы производственной площади, расход энергии, численность рабочих соответственно; — срок окупаемости капитальных затрат по r-му варианту;  — нормативный отрас­левой срок окупаемости.

В качестве ограничения могут быть и другие показатели и ха­рактеристики конкретных производств.

Анализируемое число вариантов может быть чрезвычайно ве­лико, что сделает расчет на ЭВМ не выполнимым. Поэтому задача решается по этапам. Производственный процесс разбивают на участки. Проводят оптимизацию в пределах участка. Находят подмножества     и, упорядочивая их (вводя вектор М), находят подмножества .  Из них выделяют ряд множеств , , расположенных  в  окрестностях  оптимальных  значений. При оптимизации всего производства находят множества

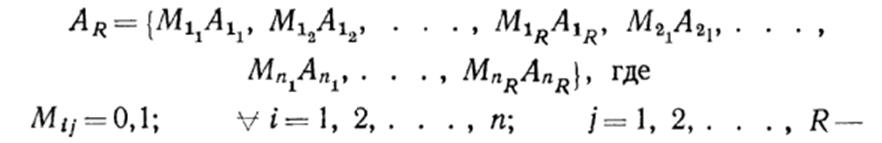
вектор, определяющий возможность получения заданного количе­ства и ассортимента продукции.

Для деревообрабатывающих производств, которые не являются фондоемкими, как показывает опыт, изменения удельных приве­денных затрат и затрат на изготовление единицы продукции имеют одинаковые закономерности [22]. Тогда оптимизационную модель можно записать в виде:

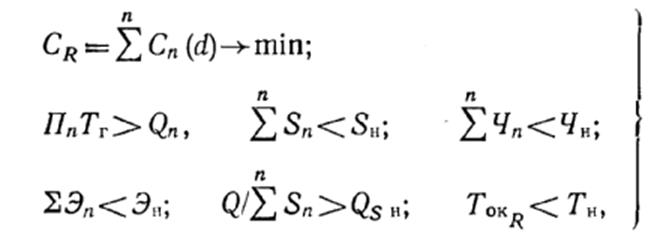
где C_n (d) — затраты на п-м участке на изготовление единицы продукции; d— функция, с помощью которой задается значение векторов  для нахождения множества ; S_n, П_п, Ч_п, Э_п — показатели R-гoварианта по n-му участку; площадь, производи­тельность, число рабочих, энергозатраты на единицу продукции;— срок окупаемости капитальных вложений по R-му ва­рианту.

Рассмотрим порядок оптимизации состава оборудования и его характеристик на n-м участке. Операторы, из которых может со­стоять участок, образуют множество

.Операторы a_nl,

i= 1, 2, . . . , l различаются или функциональным назначением, или параметрами. Множество, определяющее состав оборудования на участке, будет

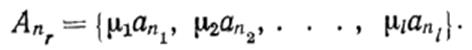
Вектор  , где — вектор, осуществляющий выбор по функциональным возможностям (Mi = 0 — оператор отсутствует; M_i = 1 — оператор используется), _mi = 1, 2, 3 ... — вектор, определяющий число i-xоператоров, необходимых для обеспечения выпуска заданного числа изделий (объема продукции). Пусть реальная фактическая производитель­ность операторов равна  .Рассмотрим случай, когда функциональное назначение всех операторов одинаково и участок имеет одинаковое оборудование. Тогда возможно получить r =lупорядоченных множеств:

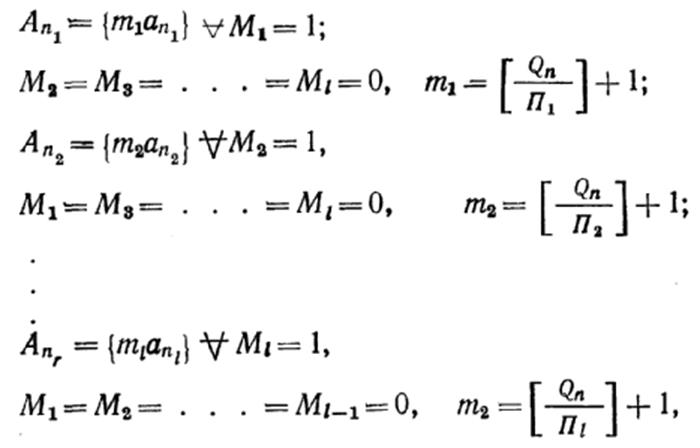
где Q_n— объем продукции на n-м участке при программе пред­приятия Q;

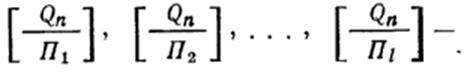
целая часть соответствующей дроби.

При условии, что на участке может использоваться оборудова­ние с различной производительностью, векторы m_iнаходят из сле­дующего:

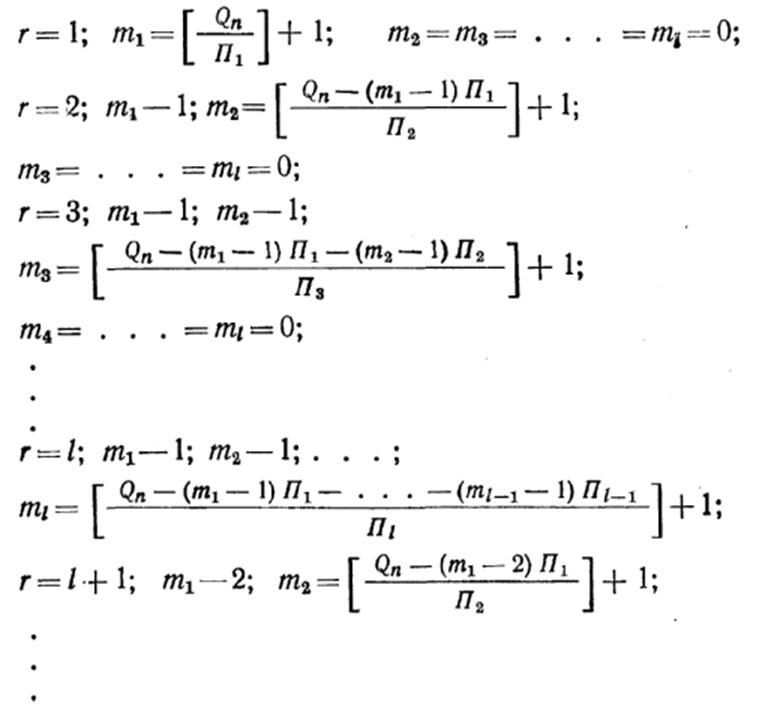
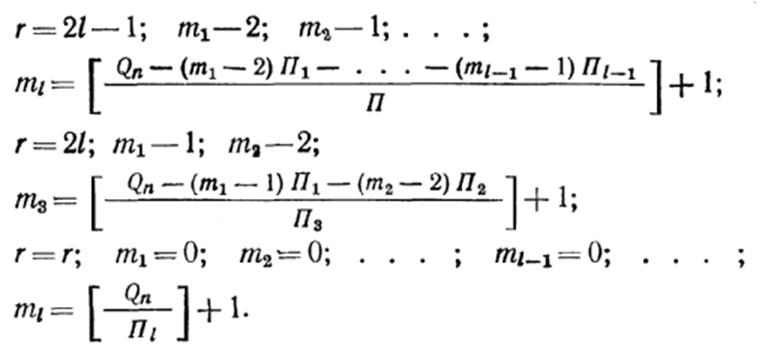
Переход от станков с индивидуальным обслуживанием к авто­матическим линиям можно представить как замену групп членов множества A_пи создание s упорядоченных множеств A_S, состоя­щих из членов — функция, опреде­ляющая порядок группирования  = 1, 2, ...,l, причем возможно . Определение характеристик, в том числе производительности, является самостоятельной задачей. Затем используя векторы M_sjи  m_sj, которые находят по условиям (28) или (29), находят множества

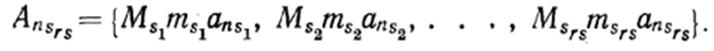
Совместный анализ множеств и позволяет решить вопрос оптимизации уровня автоматизации и состава оборудова­ния (автоматических линий) на n-м участке производства и целе­сообразности их использования. Однако оптимальный вариант на одном из участков может оказаться неудовлетворительным при оптимизации всего производства, так как объективно функцией dс оптимальным вариантом по одному участку могут сопрягаться худшие варианты по смежным участкам. Поэтому при оптимизации участка необходимо знать данные не только для лучшего, но и для других вариантов, представляющих интерес с точки зрения оптимизации производства. Обычно это варианты, однозначно опреде­ляющие выбор вариантов по смежным участкам. Например, в ме­бельном производстве облицовывание плит пластиком исключает необходимость их шлифования и отделки.

Определим, из чего складываются затраты на n-м участке на изготовление продукции по r-му и r_s-му  вариантам. Для упроще­ния индексы п, г и r_sопустим. Тогда затраты на выпуск единицы продукции

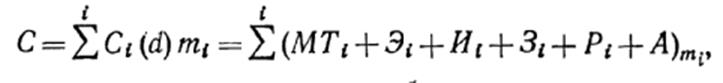
где C_i— затраты, связанные с преобразованием материала в про­дукцию i-м оператором; затраты: d— функция, определяющая выбор значений i(из каких операторов состоит участок); MT_i— на материал на единицу продукции; Э_i— на энергию на единицу продукции; И_i— на инструмент и приспособления; P_i— на ремонт и техническое обслуживание; З_i— заработная плата рабочих; A_i— амортизационные отчисления на полное восстановление обо­рудования и производственных помещений.