Анализ автоматической системы регулирования и расчет настроек регулятора

2.2 Анализ АСР и расчет настроек регулятора

Увеличение требований к качеству ведения технологического процесса обуславливает широкое внедрение микропроцессорных систем автоматического регулирования различной степени сложности. Значительное место среди них занимают контроллеры, которые обеспечивают выполнение задач автоматического регулирования.

В рассматриваемом технологическом процессе осуществляется регулирование уровня в дополнительном баке (лист АПП.000001.052.А2).

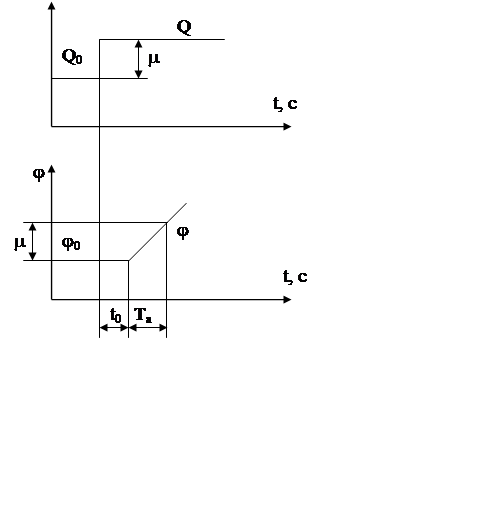
Рассмотрим работу дополнительного бака более подробно. На рисунке 2.1  показан бак, в котором регулирование уровня осуществляется воздействием на отток рабочей среды. [   ].

 

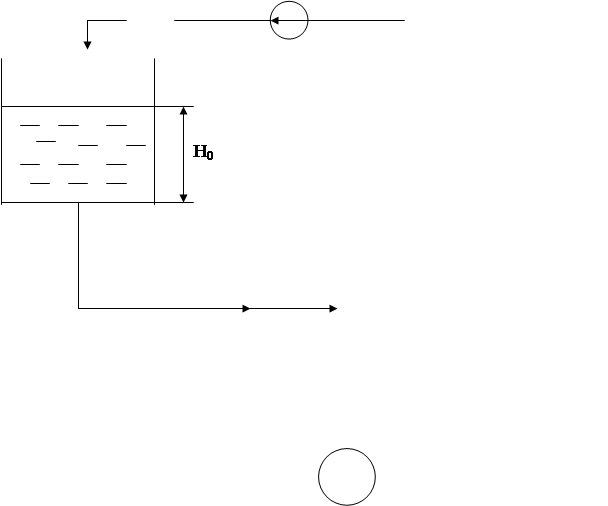Рисунок  2.1 - Одноемкостный объект без самовыравнивания

На притоке и на расходе установлены насосы, ввиду чего данный объект не обладает самовыравниванием.

Рассматриваемый объект является астатическим, математически он описывается уравнением (2.1), которому отвечает разгонная характеристика на рисунке 2.2

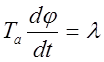,                                                 (2.1)

где     Т_а – условная постоянная времени разгона объекта, с;

           l - относительная величина возмущающего воздействия;

           j - относительная величина регулируемого параметра;

Q

            t – время.

 

Рисунок  2.2 - Разгонная характеристика объекта без самовыравнивания

Условная постоянная времени определяется по формуле

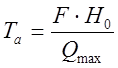 ,                                             (2.2)

где      F     – поперечное сечение бака, м²;

           Q_max – максимальное значение расхода, м³/с;

           H₀ – номинальное значение уровня жидкости в баке, м.

Подставляем параметры технологического процесса в формулу (2.2), получаем:

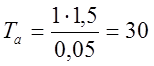 с

Время транспортного запаздывания находим по формуле:

t₀=0,05*Т_а ,                                                   (2.3)

t₀=0,05*30=1,5 с

Передаточную функцию объекта без самовыравнивания берем из [  ] , которая имеет вид:

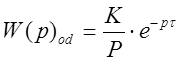 ,                                              (2.4)

где      К – коэффициент усиления;

           t - транспортное запаздывание, с.

Коэффициент усиления находим по формуле:

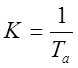,                                                        (2.5)

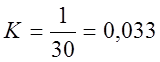 с^-1

В качестве закона регулирования используем пропорционально-интегральный закон, так как у систем с ПИ – регулятором отсутствует статическая ошибка и хорошие динамические свойства.

Передаточную функцию ПИ – регулятора берем из [ ], которая описывается выражением:

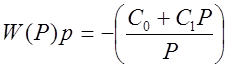,                                           (2.6)

где      С₀,С₁ – параметры настройки регулятора.

2.3.1 Расчет оптимальных параметров настройки регулятора    

методом расширенной АФХ

Существует большое количество различных методов расчета параметров настройки регуляторов (ПНР), которые отличаются друг от друга точностью и объемом вычисления. Для расчета настроек нашего регулятора будем использовать метод расширенной амплитудно – фазной характеристики (АФХ), так как этот метод получил наибольшее распространение в инженерной практике наладки промышленных систем регулирования.

Путем замены P=(i-m)w определяем расширенную амплитудно – фазовую характеристику объекта W(m;iw)_об. Модуль колебательности m берем из [ ]: m=0,221. Данному значению модуля соответствует степень затухания y=0,75, которую также берем из [  ].

После замены Р на (i-m)w расширенная АФХ объекта примет вид:

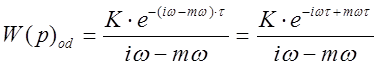,                                 (2.7)

Разлагаем расширенную АФХ на действительную и мнимую части:

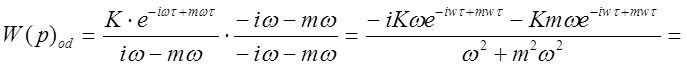
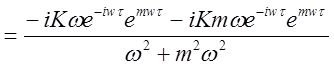                                   (2.8)

Так как е^-iwt = coswt-sinwt, то выражение (2.8) примет вид:

.

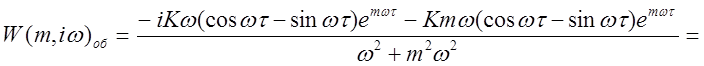
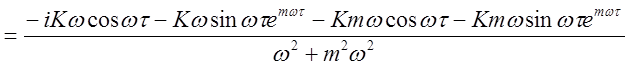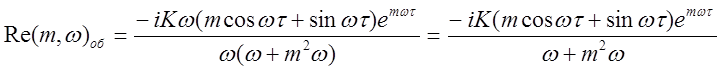,        (2.9)

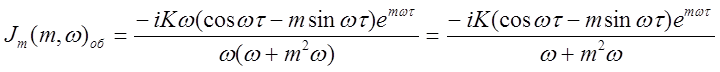,      (2.10)

Проводим замену Р на (i-m)w для определения АФХ регулятора W(m,iw)p.

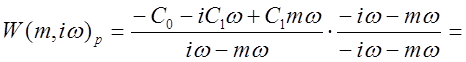
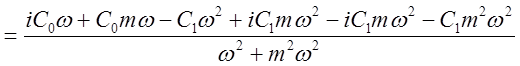,                    (2.11)

Из выражения (2.11) выделяем вещественную и мнимую части:

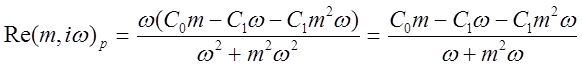,               (2.12)

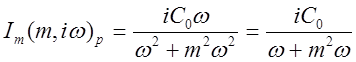.                             (2.13)

Вещественная и мнимая части регулятора в зависимости от m,w,С₀,С₁ имеют соответственно вид:

,                           (2.14)

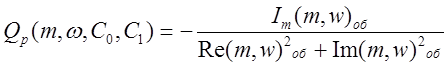.                          (2.15)

Приравниваем выражения (2.14) и (2.15) к выражениям (2.9) и (2.10) соответственно, получаем:

.

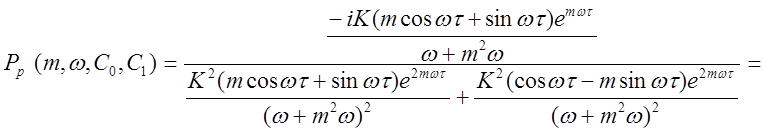
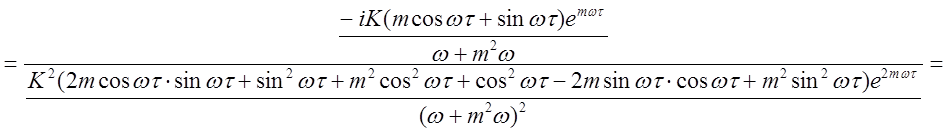
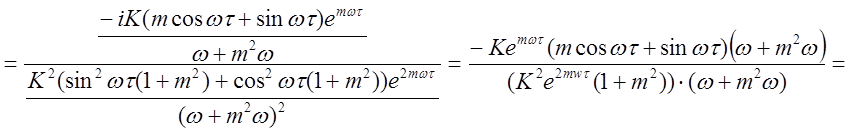
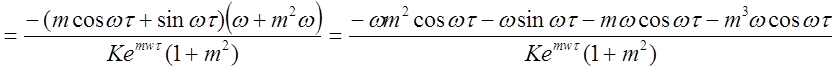Таким образом вещественная часть регулятора описывается выражением:

.               (2.16)

Находим мнимую часть регулятора:

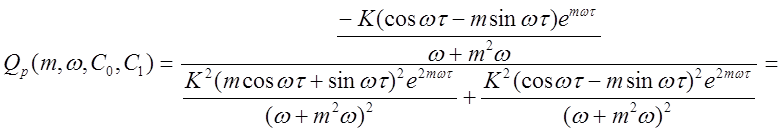
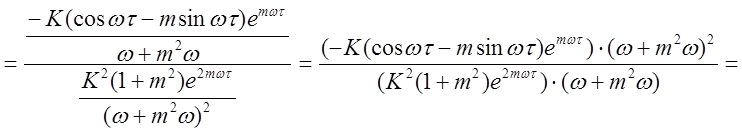
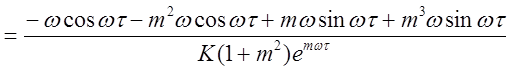.                         (2.17)

Приравняем выражения (2.13) и (2.17), получаем:

,

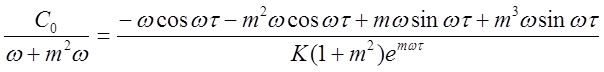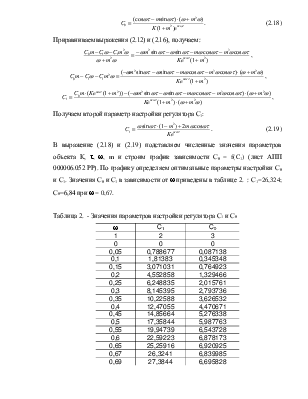
Из уравнения (2.18) выделяем параметр настройки регулятора С₀:

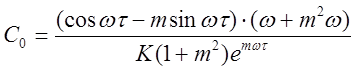.                                    (2.18)

Приравниваем выражения (2.12) и (2.16), получаем:

,

,

,

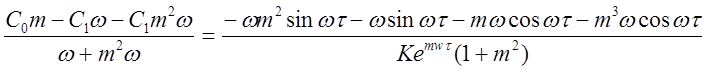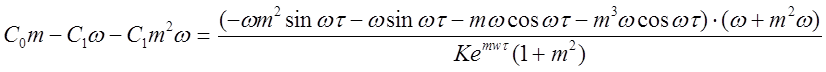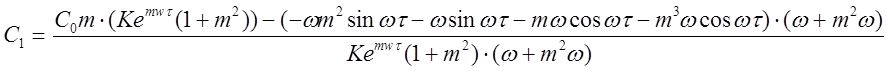Получаем второй параметр настройки регулятора С₁:

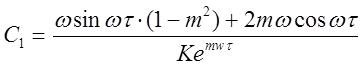.                                (2.19)

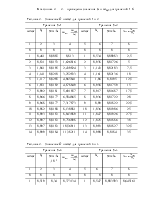
В выражение (2.18) и (2.19) подставляем численные значения параметров объекта К, t, w, m и строим график зависимости С₀ = f(C₁) (лист АПП 000006.052 РР). По графику определяем оптимальные параметры настройки С₀ и С₁. Значения С₀ и С₁ в зависимости от w приведены в таблице 2.  : С₁=26,324; С₀=6,84 при w = 0,67. 

Таблица 2.  - Значения параметров настройки регулятора С₁ и С₀

	w	C1	C0
	1	2	3
	0	0	0
	0,05	0,788677	0,087138
	0,1	1,81383	0,345348
	0,15	3,071031	0,764923
	0,2	4,552858	1,329466
	0,25	6,248835	2,015761
	0,3	8,145395	2,793736
	0,35	10,22588	3,626532
	0,4	12,47055	4,470671
	0,45	14,85664	5,276338
	0,5	17,35844	5,987763
	0,55	19,94739	6,543728
	0,6	22,59223	6,878173
	0,65	25,25916	6,920925
	0,67	26,3241	6,839985
	0,69	27,3844	6,695828
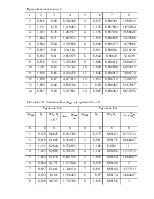
Продолжение таблицы 2.
	1	2	3
	0,7	27,91204	6,598522
	0,75	30,51262	5,835159
	0,8	33,02079	4,553715
	0,85	35,39486	2,676893
	0,9	37,5919	0,128429
	0,91	38,00622	-0,46842