Задание на проектирование
1. Преобразование структурной схемы и определение передаточных функций разомкнутой и замкнутой системы.
2. Исследование системы на устойчивость.
3. Выбор системы и параметров корректирующих устройств с учетом заданных показателей качества переходного процесса.
Реферат
В данной курсовой работе произведен расчёт линейной АСР на устойчивость.
Для проверки АСР на устойчивость были применены критерии: Рауса, Гурвица, Михайлова, Найквиста и логарифмический метод.
Расчет выполнен с учетом заданных показателей качества переходного процесса. По результатам расчета был произведен выбор системы и параметров корректирующего устройства.
Пояснительная записка выполнена в текстовом редакторе Word, которое является приложением Microsoft Office XP, также был использован пакет MathCAD.
Курсовая работа содержит пояснительную записку из 19 страниц текста, 6 таблиц, 5 графиков, 2 рисунков и из 4 литературных источников.
Введение. . . . . . . . . . . 5
1. Анализ исходных данных и составление передаточной
функции разомкнутой системы. . . . . . . 6
2. Исследование системы на устойчивость. . . . . 7
2.1 Исследование АСР на устойчивость по
критерию Гурвица. . . . . . . 7
2.2 Исследование АСР на устойчивость по
критерию Рауса. . . . . . . . 8
2.3 Исследование АСР на устойчивость по
годографу Михайлова. . . . . . . 9
2.4 Исследование АСР по критерию Найквиста. . . 10
2.5 Исследование АСР по логарифмическим
частотным характеристикам. . . . . . 12
3.Выбор схемы и параметров корректирующих
устройств с учетом заданных показателей
переходного процесса методом логарифмических
частотных характеристик. . . . . . . . 14
4.Проверка скорректированной системы по
критерию Рауса. . . . . . . . 16
Заключение. . . . . . . . . . 17
Список использованной источников. . . . . . 18
Введение
Синтез Автоматической системы регулирования осуществляется в два этапа: частотный метод синтеза корректирующего устройства; расчёт переходного процесса.
При синтезе системы непрерывного регулирования по отклонению основы её структуры уже заданы. В таком случае характерны два варианта постановки задачи синтеза.
1). Выбор некоторых параметров (вероятнее всего передаточного коэффициента разомкнутой системы и постоянных времени корректирующих устройств).
2). Выбор части параметров и уточнение структуры: выбор местных обратных связей, выбор корректирующих устройств.
Чаще всего задача сводится к выбору структуры и параметров корректирующего устройства, т.е. к синтезу корректирующего устройства. Основная задача корректирующего устройства – улучшение точности системы и качества переходных процессов и наряду с этим решить и более общую задачу – сделать систему устойчивой, если она была без корректирующего устройства неустойчивой, а затем добиться и желаемого качества процесса регулирования. Наиболее распространен частотный метод синтеза корректирующих устройств с помощью ЛЧХ. Существует методика расчёта последовательного и параллельного корректирующих устройств.
Метод определения переходных процессов можно разбить на две основные группы:
1). Способы решения дифференциальных уравнений (аналитические, графические, графо – аналитические), из которых наибольшее распостронение получил операторный метод, основанный на использовании преобразования Лапласа.
2). Способы, основные на использовании частотных характеристик АСР. Наиболее известным является метод построения кривой переходного процесса с помощью трапециидальных вещественных частотных характеристик и метод аппроксимации вещественной частотной характеристики отрезками прямых.
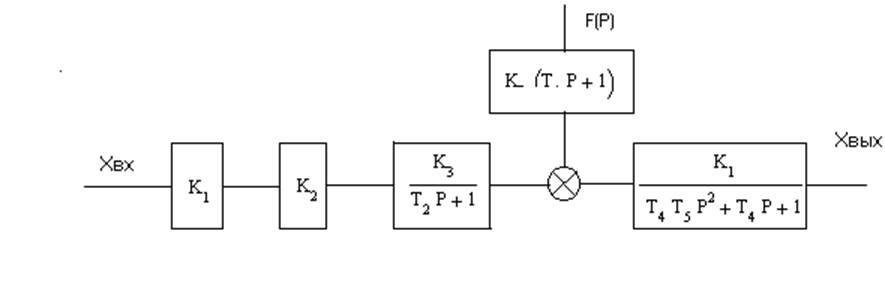
Рисунок 1
К=0,09
К=415
К=1,58
К=5,6
Т=0,065 сек.
Т=0,081 сек.
Показатели качества: 1) время регулирования: 1,4
2) перерегулирование: 30%
Корректирующее устройство: параллельное
Передаточная функция замкнутой АСР
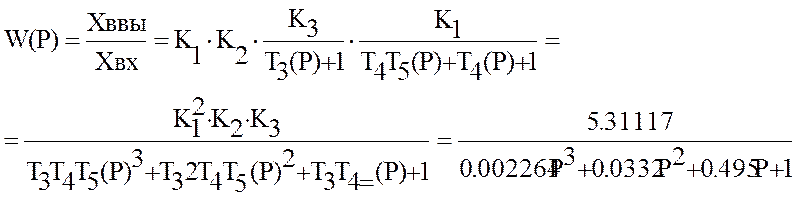
![]()
Критерий Гурвица относится к алгебраическим корням, проверка устойчивости сводится к выполнению по коэффициентам характеристического уравнения, так называемым определителям Гурвица, для получения которых составляют квадратичную матрицу из коэффициентов характеристического уравнения.
Записываем передаточную функцию разомкнутой АСР.

![]()
Выделить характеристическое уравнение замкнутой АСР.
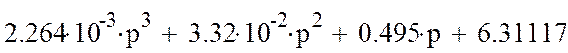
Составить квадратичную матрицу из коэффициентов характеристического уравнения. Вычислить определители матрицы.
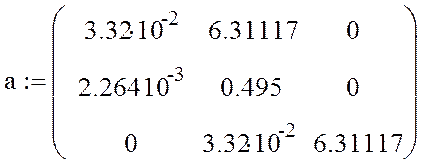
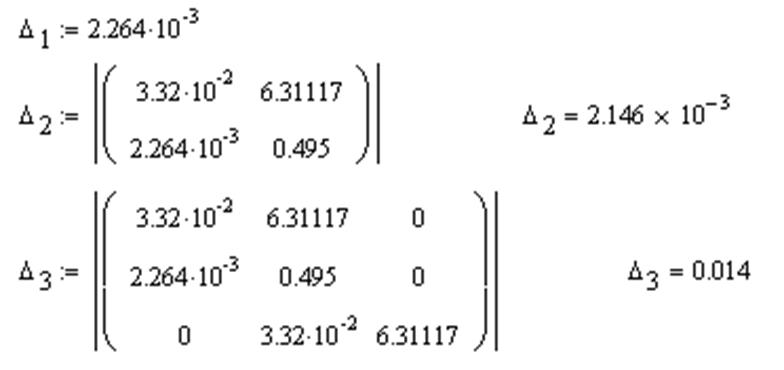
Система устойчива, т. к. у системы все определители положительные.
2.2 Исследование АСР на устойчивость по критерию Рауса.
Практически критерием Гурвица выгодно пользоваться при исследовании устойчивости система автоматического управления не выше пятого порядка. Для системы более высоких порядков удобнее принять критерий Рауса. Для определения устойчивости по коэффициентам характеристического уравнения замкнутой системы Рауса предложил правило, оформленное в виде таблицы.
Записываем передаточную функцию разомкнутой АСР.
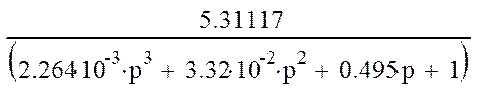
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.