Выделить характеристическое уравнение замкнутой АСР.
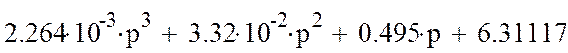
Составляем таблицу Рауса.1
|
a0 |
a 2 |
|
a1 |
a 3 |
|
|
|
|
|
|
|
0,002264 |
0,495 |
|
0,0332 |
6,31117 |
|
0,065 |
0 |
|
11,454 |
0 |
Система устойчива т. к. все коэффициенты первого столбца положительны.
2.3 Исследование АСР на устойчивость по годографу Михайлова.
Согласно критерию Михайлова, для устойчивости системы автоматического регулирования n-го порядка необходимо и достаточно, чтобы годограф Михайлова, начав движение от вещественной положительной оси комплексной плоскости, обошёл в положительном направление последовательно n-квадратов, нигде не обращаясь в 0.
Записываем передаточную функцию разомкнутой АСР

Выделить характеристическое уравнение замкнутой АСР.
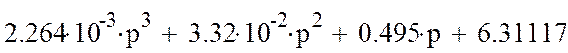
Выделим действительную и мнимую часть.
![]()
![]()
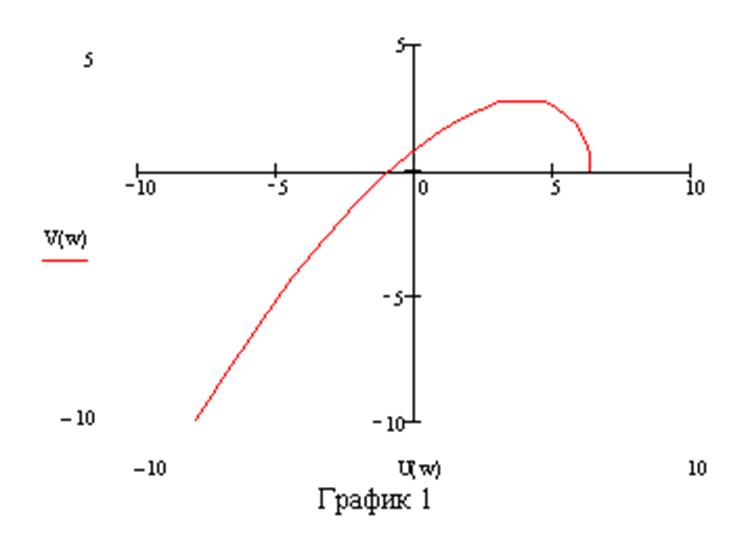
Система устойчива т. к. годограф последовательно обходит 3 квадранта не обращаясь в 0.
2.4 Исследование АСР на устойчивость по критерию Найквиста.
Критерий Найквиста базируется на частотные характеристиках разомкнутой цепи система автоматического регулирования и даёт правила, согласно которым по виду АФХ разомкнутой системы можно судить об устойчивости системы.
Различают три случая применения критерия Найквиста.
1. Разомкнутая система устойчивая. В этом случае корни характеристическое полинома разомкнутой АСР отрицательны.
2. И для устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой системы не охватывала точку с координатами (-1, 0).
3. Разомкнутая система на границе устойчивости. Характеристический полином такой системы имеет нулевые или чисто мнимые корни, а у остальных корней отрицательные вещественные части.
4. Разомкнутая система неустойчивая. Характеристический полином такой системы имеет корни с положительной вещественной частью, остальные корни имеют отрицательные вещественные части.
Записываем передаточную функцию разомкнутой АСР.

Выделить характеристическое уравнение замкнутой АСР.
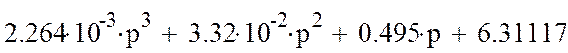
Определим частотную передаточную фцнкцию системы регулирования. Выделим мнимую и вещественную части, для чего числитель и знаменатель передаточной функции, записанной в частотной форме, умножим на сопряженное число. Подставим числовые значения получим:
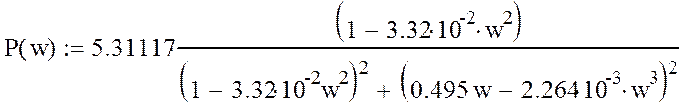
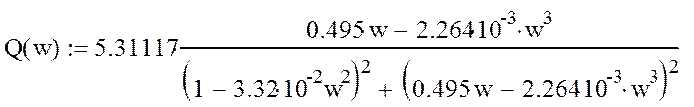
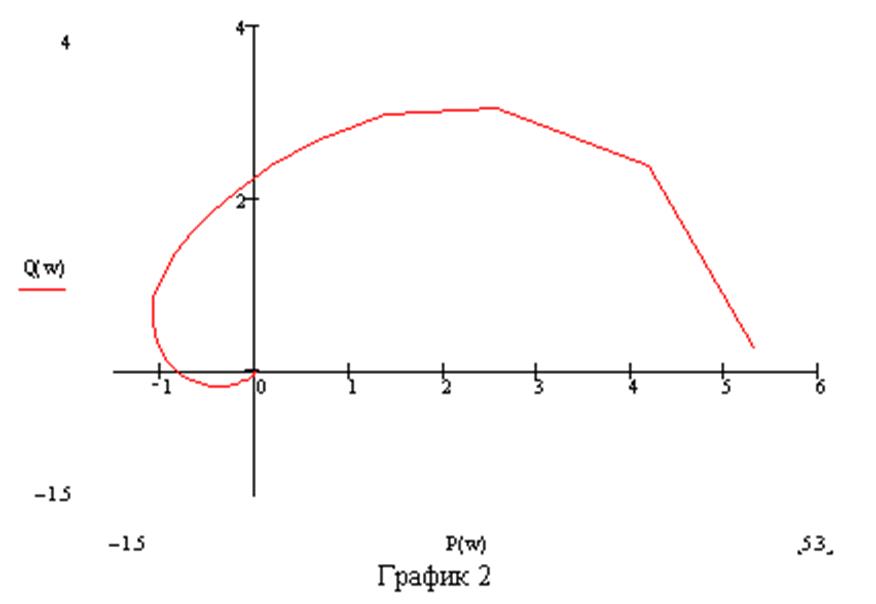
Система устойчива т. к. дуга не охватывает точку с координатами –1,j0
Для определения устойчивости замкнутой АСР по логарифмическим частотным характеристикам разомкнутой системы необходимо выполнить следующие операции:
1. Выделить структурную схему разомкнутой системы разомкнутой АСР.
2. Записать передаточную функцию разомкнутой системы.
3. Построить ЛАЧХ и ЛФЧХ в соответствии с алгоритмами для построения этих характеристик.
4. По ЛАЧХ и ЛФЧХ выяснить устойчивость замкнутой АСР. Для устойчивости системы в замкнутом состоянии необходимо и достаточно, чтобы число переходов ЛФЧХ через линию –1800 при положительных значениях ЛАЧХ было чётным.
Алгоритм построения ЛАЧХ разомкнутой статической системы методом асимптот.
Передаточная функция разомкнутой системы регулирования равна:

Выделим мнимую и вещественную части:
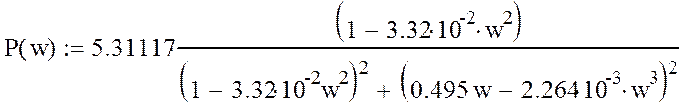
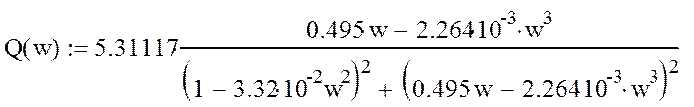
Строим ЛАЧХ и ЛФЧХ:
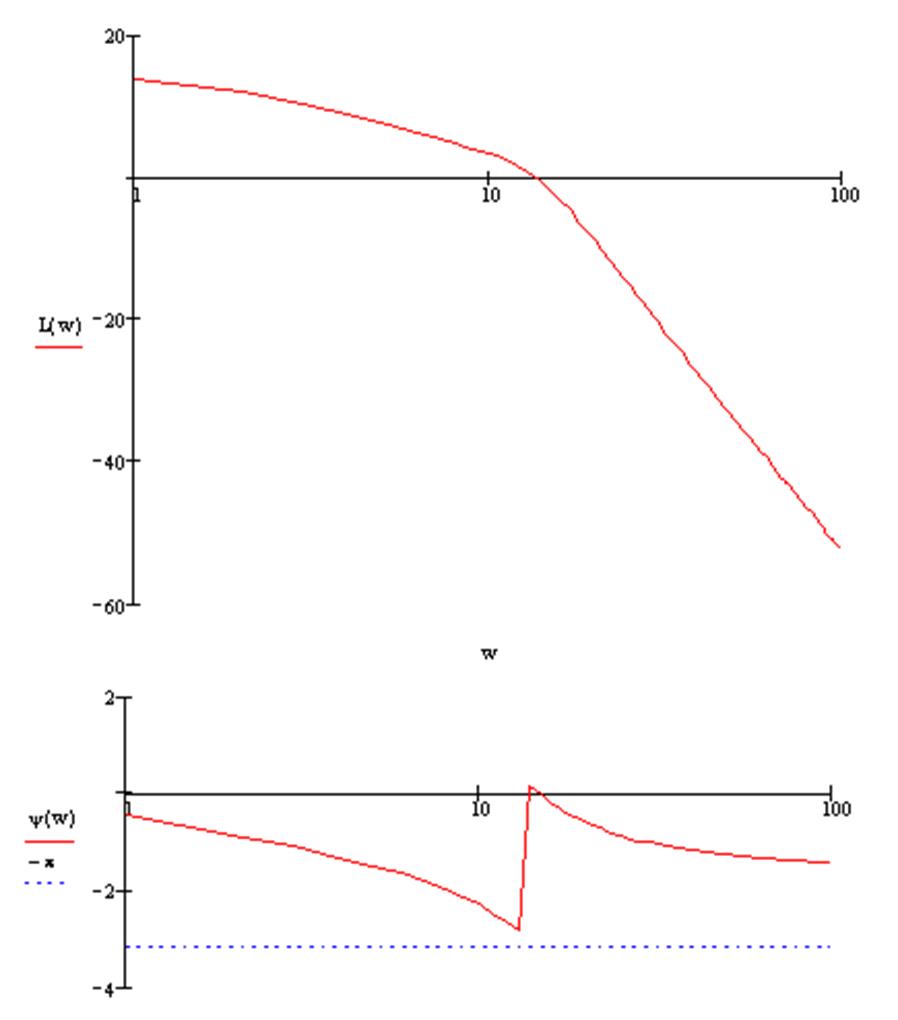
ЛФЧХ при положительных значениях ЛАЧХ не пересекает линию -1800С, следовательно, система устойчива.
3. Выбор схемы и параметров корректирующих устройств с учетом заданных показателей переходного процесса методом логарифмических частотных характеристик
Строим ЛАЧХ исходной некорректируемой системы Lн (w). В той же координатной системе строим желаемую ЛАЧХ Lж(w), то есть характеристику скорректированной системы. Путем вычитания ординат исходной ЛАЧХ из ординат желаемой ЛАЧХ получаем ЛАЧХ корректирующего звена
Lк(w)=Lж(w)-Lн(w)
![]()
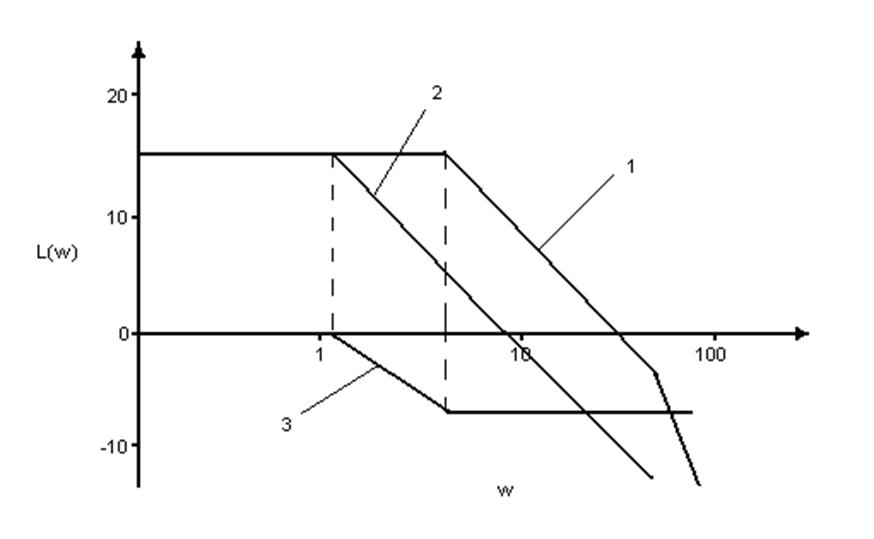
График 5
1.Полученная ЛАЧХ
2.Желаемая ЛАЧХ
3.ЛАЧХ корректирующего устройства.
По виду ЛАЧХ выбираем корректирующее устройство.
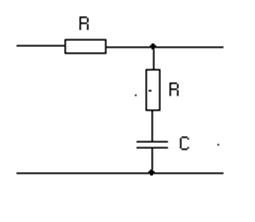 |
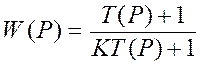
![]() =0,0435
=0,0435
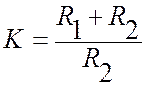 =10
=10
![]() Рисунок 2
Рисунок 2
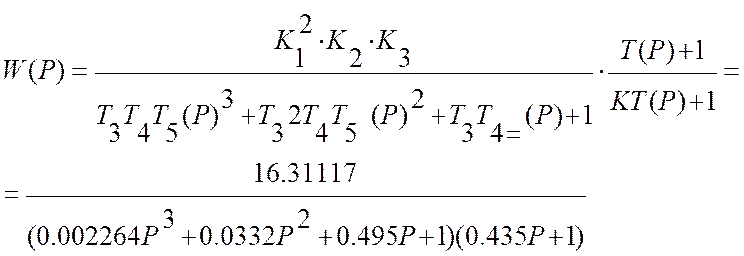
Записать передаточную функцию замкнутой АСР.
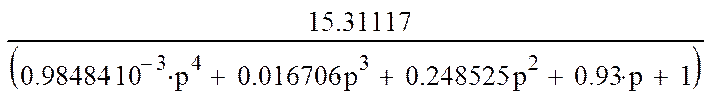
Выделить характеристическое уравнение замкнутой АСР.
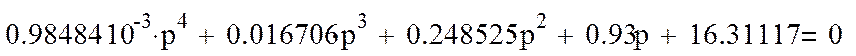
Составим таблицу 6
|
0,000985 |
0,249 |
16.31117 |
|
0,0167 |
0,93 |
0 |
|
0,194 |
9,216 |
0 |
|
16,31117 |
0 |
0 |
|
9,216 |
0 |
0 |
Система устойчива т. к. все коэффициенты первого столбца положительны.
Заключение
В результате выполнения курсовой работы мы исследовали исходную систему на устойчивость по различным критериям: Гурвица, Рауса, Михайлова, Найквиста и ЛАЧХ. Произвели выбор схемы и параметров корректирующего устройства. Построили вещественную частотную характеристику системы.
Список использованных источников
1. Теория автоматического управления: Учеб. Для вузов по спец. «Автоматика и телемеханика». В 2-х ч. / А. А. Воронов, Д. П. Ким, В. М. Лохин и др.; Под редакцией А. А.Воронова.-2-е изд., перераб. и доп. –М.: Высш. Шк.,1986.-504с.,ил.
2. «Теория автоматического управления»/ В. Н. Брюханов, М. Г. Косов, Ю. М. Соломенцев и др.: . –М.: Высш. Шк.,2000.-265с.,ил.
3. Методические указания к выполнению курсовой работы «Анализ и синтез линейных систем автоматического регулирования».-Министерство высшего и среднего специального образования.-Сиб.ТИ.-Красноярск.-1986.
4. Стандарт предприятия. Система вузовской учебной документации «Требования к оформлению текстовых документов».-К.: 2001.-45с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.