Другие предметы \ Теория автоматического управления

Анализ автоматической системы регулирования и расчет настроек регулятора, страница 2

Из [ ] С₀ и С₁ определяются по выражению (2.20) и (2.21) соответственно.

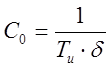, (2.20)

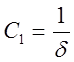. (2.21)

Из выражения (2.21) находим d:

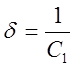, (2.22)

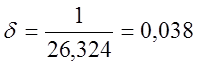Из выражения (2.20) находим Т_и:

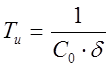, (2.23)

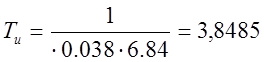Таким образом, время изодрома Т_и и установленный коэффициент пропорциональности d соответственно равны Т_и = 3,8485, d = 0,038.

2.3.2 Построение переходного процесса системы регулирования

Довольно часто после определения значений настроечных параметров автоматического регулятора желательно получить непосредственно картину переходного процесса. Существуют различные способы построения кривых переходного процесса в системах автоматического регулирования.

В нашем случае построение кривых переходного процесса будем осуществлять наиболее распространенным методом трапецеидальных характеристик. Для этого проведём ряд преобразований.

Определяем АФХ замкнутой системы по возмущающему воздействию.

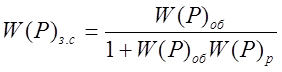, (2.24)

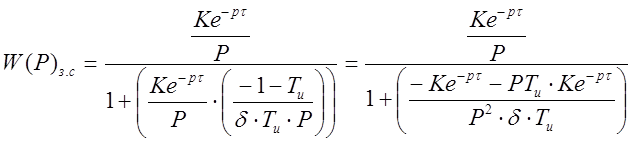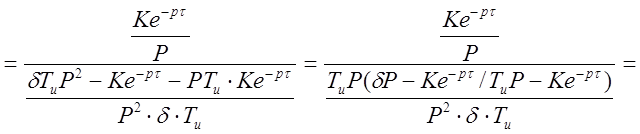
Таким образом передаточная функция замкнутой системы регулирования описывается выражением :

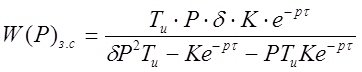, (2.25)

Проведем замену Р на iw, получим:

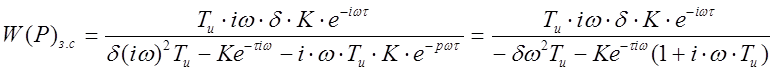, (2.26)

Так как е^-i^w^t= coswt-sinwt, то выражение (2.3.26) примет вид:

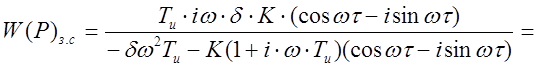
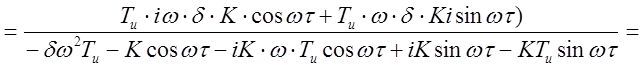
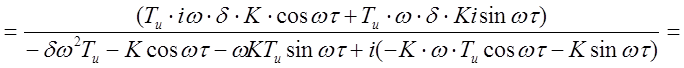
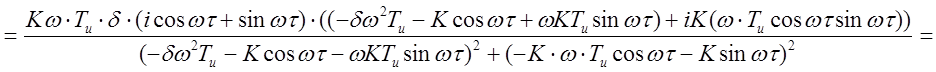
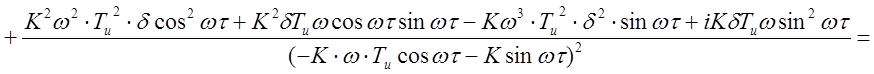
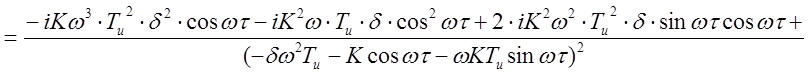
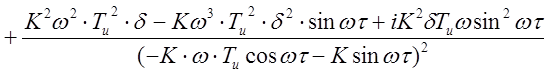, (2.27)

Из (2.27) выделяем вещественную и мнимую части:

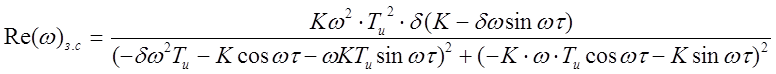, (2.28)

Подставим в выражение (2.28) вместо К, d, Т_и, t их численные значения, получим:

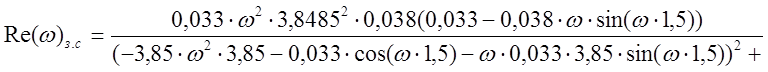
Значения Re(w)_з.с в зависимости от частоты (w) приведены в таблице

Таблица 2. - Значения действительной части (Re(w)_з.с ) в зависимости от w

w	R_e(w)	w	R_e(w)
0	0	0,7	0,016646
0,1	0,0025	0,8	0,011857
0,2	0,008	0,9	0,0105
0,3	0,015315	1	0,0054
0,4	0,017483	1,6	-0,00623
0,5	0,018401	3	0,0015
0,6	0,018266	5	0,0003

По данным таблицы 2. строим график вещественной частотной характеристики (ВЧХ) (лист АПП.000006.052 РР).

Заменяем график ВЧХ мало отличающейся ломанной кривой (лист АПП.000006.052 РР), т.е. кривую разбиваем на трапеции. Обязательным условием разбивки является то, что все трапеции одной стороной должны прилегать к оси ординат. Для этого ко всем точкам перегиба ВЧХ строим касательные, затем строим касательные к наклонным участкам ВЧХ, а полученные точки пересечения касательных будут являться вершинами трапеций.

При разбивке количество трапеций должно быть минимальным, но при этом площадь, ограниченная трапециями должна максимально соответствовать площади под кривой ВЧХ.

В результате замены кривой ломанной линией получаем пять трапеций (лист АПП.000006.052 РР). В местах где значение амплитуды ВЧХ не превышает одной десятой от максимальной, разбивку не делаем, так как площадь этих трапеций будет незначительна.

Параметры трапеций сведены в таблицу 2. .

Таблица 2. - Параметры трапеций

№ тра-пеции	r₀	w₁	w₀
1	00184	1,23	0,63	0,51
2	-0,0184	0,4	0,4	1
3	-0,0066	2,68	1,87	0,7
4	0,0066	1,55	1,23	0,79
5	0,0018	5,2	3,75	0,72
6	-0,0018	3	2,68	0,89

Для каждой трапеции выбираем интервал Dt_табл и определяем по таблицам [ ] значения h_x. Умножаем r₀ наh_x и получаем значения ординат G=r_0*h_x, соответствующих истинным интервалам времени Dt_ист = Dt_табл/w₁.

В таблицах 2. – 2. приведены значения G и Dt_ист для трапеций 1-6.

Таблица 2. - Значение G и Dt_ист для трапеций 1 и 2

Трапеция №1				Трапеция №2
Dt_табл	h_x	d=r_0*h_x		Dt_табл	h_x	d=r_0*h_x
1	2	3	4	5	6	7	8
0	0	0	0	0	0	0	0
1	0,461	0,0085	0,813	1	0,534	-0,00983	2,5
2	0,831	0,0153	1,626016	2	0,938	-0,01726	5
3	1,061	0,0195	2,439024	3	1,143	-0,02103	7,5
4	1,141	0,0210	3,252033	4	1,161	-0,02136	10
5	1,117	0,0205	4,065041	5	1,06	-0,0195	12,5
6	1,051	0,0192	4,878049	6	0,956	-0,01759	15
7	0,992	0,0181	5,691057	7	0,917	-0,01687	17,5
8	0,966	0,0177	6,504065	8	0,936	-0,01722	20
9	0,968	0,0177	7,317073	9	0,99	-0,01822	22,5
10	0,982	0,0180	8,130081	10	1,036	-0,01906	25
11	0,993	0,0183	8,943089	11	1,047	-0,01926	27,5
12	0,997	0,0183	9,756098	12	1,025	-0,01886	30
13	0,997	0,0183	10,56911	13	0,993	-0,01827	32,5
14	0,999	0,0184	11,38211	14	0,990	-0,0184	35

1 2 3

Скачать файл