Оптимальные системы автоматического управления

ОПТИМАЛЬНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

Постановка задачи оптимизации управления

В общем случае автоматическая система состоит из объекта управления и совокупности устройств, которые обеспечивают управление этим объектом. Как правило, эта совокупность устройств включает в себя измерительные устройства, усилительные и преобразовательные устройства,  а также исполнительные устройства. Если объединить эти устройство в одно звено (управляющее устройство), то структурная схема системы выглядит следующим образом:

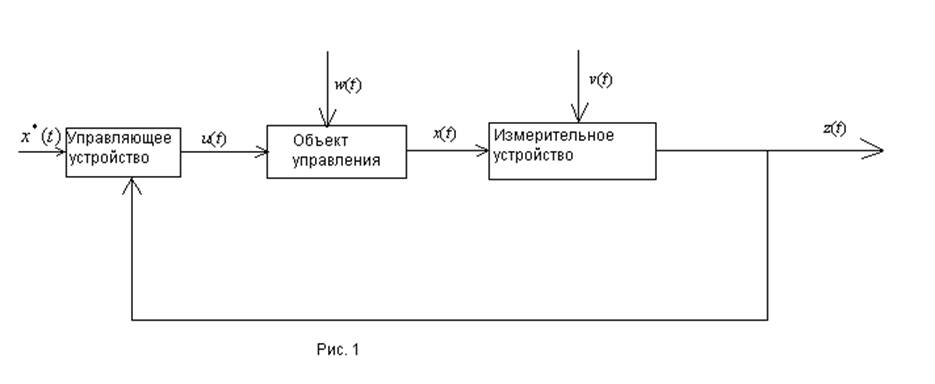
В автоматической системе информация о состоянии объекта управления через измерительное устройство поступает на вход управляющего устройства. Такие системы называются системами с обратной связью или замкнутыми системами. Отсутствие этой информации в алгоритме управления говорит о том, что система разомкнута. Состояние объекта управления в любой момент времени будем описывать  переменными , которые называются координатами системы или переменными состояния. Их удобно считать координатами - мерного вектора состояния .

Измерительное устройство выдает информацию о состоянии объекта. Если на основании измерения вектора  могут быть найдены значения всех координат  вектора состояния , то говорят, что система полностью наблюдаема.

Управляющее устройство вырабатывает управляющее воздействие . Таких управляющих воздействий может быть несколько, они образуют - мерный управляющий вектор .

На вход управляющего устройства поступает задающее входное воздействие . Это входное воздействие несет информацию о том, какое должно быть состояние объекта. На объект управления может действовать возмущающее воздействие , которое представляет собой нагрузку или помеху. Измерение координаты объекта, как правило, осуществляется с некоторыми погрешностями , которые тоже носят случайный характер.

Задачей управляющего устройства является выработка такого управляющего воздействия , чтобы качество функционирования автоматической системы в целом было бы наилучшим в некотором смысле.

Мы будем рассматривать такие объекты управления, которые являются управляемыми. То есть вектор состояния можно изменять требуемым образом путем соответствующего изменения вектора управления. Будем подразумевать, что объект полностью наблюдаемый.

Так, например, положение летательного аппарата характеризуется шестью координатами состояния. Это - координаты центра масс, - углы Эйлера, определяющие ориентацию летательного аппарата относительно центра масс. Положение летательного аппарата можно изменить с помощью рулей высоты, курса, элерона и с помощью уклонения вектора силы тяги. Таким образом управляющий вектор определен следующим образом:

- угол отклонения рулей высоты

- курс

- элерон

 - тяга

Вектор состояния в этом случае определяется следующим образом:

Можно поставить задачу выбора управления, с помощью которого летательный аппарат переводится из заданного начального состояния  в заданное конечное состояние  с минимальными затратами топлива или за минимальное время.

Дополнительная сложность при решении технических задач возникает в силу того, что на управляющее воздействие и на координаты состояния объекта управления, как правило, накладываются различные ограничения.

На любой угол рулей высоты, курса, элерона существуют ограничения:

  

 - тяга сама по себе ограничена.

На координаты состояния объекта управления и их производные также накладываются ограничения, которые связаны с допустимыми перегрузками.

Мы будем рассматривать объекты управления, которые описываются дифференциальным уравнением:

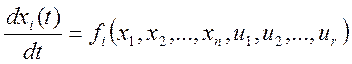
     (1)

Или в векторном виде:

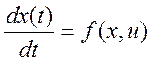
Здесь:

 - -мерный вектор состояния объекта

 - -мерный вектор управляющих воздействий

- функция правой части уравнения (1)

На вектор управления  накладывается ограничение, мы будем полагать, что его значения принадлежат некоторой замкнутой области  некоторого -мерного пространства. Это означает, что управляющая функция   в любой момент времени принадлежит области ().

Так, например, если координаты управляющей функции удовлетворяет неравенствам:

 

то область  является -мерным кубом.

Назовем допустимым управлением всякую кусочно-непрерывную функцию , значения которой в каждый момент времени  принадлежит области , и которая может иметь разрывы первого рода. Оказывается, даже в некоторых задачах оптимального управления решение может быть получено в классе кусочно-непрерывного управления. Для того, чтобы выбрать управление как функцию времени и начального состояния системы , которое однозначно определяет движение объекта управления, требуется, чтобы система уравнений (1) удовлетворяла условиям теоремы существования и единственности решения в области . В этой области располагаются возможные траектории движения объекта и возможные управляющие функции . Если область изменения переменных является выпуклой, то для существования и единственности решения достаточно, чтобы функции  . были непрерывны по всем аргументам и имели непрерывные частные производные по переменным  .

В качестве критерия, который характеризует качество работы системы, выбирается функционал вида:

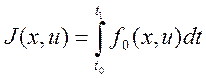   (2)

В качестве функции будем предполагать, что она непрерывна по всем своим аргументам и имеет непрерывные частные производные по  .

Критерии оптимизации

В зависимости от вида подынтегральной функции функционала:

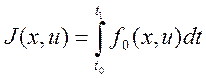  (1)

могут быть получены различные критерии применяемой проектируемой автоматической системой.

Одним из наиболее распространенных критериев является время переходного процесса объекта управления из заданного начального состояния  в конечное состояния . Чтобы получить критерий, нужно положить подынтегральную функцию:

Тогда мы получим следующий критерий оптимизации:

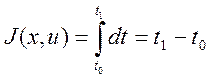   (2)

Другой широко распространенный критерий оптимальности – это квадратичный критерий:

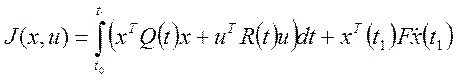   (3)

Здесь:

,  и - симметричные матрицы соответствующих размерностей ,,;

 - символ транспонирования.

Другой функционал:

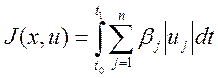   (4)

Здесь,  - это весовые координаты. Эти координаты позволяют учесть расход рабочего тела на управление. Задачи, решение которой минимизировалось в процесс (4), называются задачами САУ по расходу топлива. Такие задачи возникают, например, при управлении космическими аппаратами, когда существенной является экономия расходования горючего на борту аппарата.

Иногда в практике проектирования рассматривается функционал:

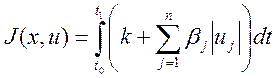   (5)

Здесь и  удовлетворяют неравенствам .

Этот функционал является комбинацией функционалов (2) и (4) и позволяет учесть как время переходного процесса, так и расход топлива.

Выбор того или иного функционала определяется и техническими показателями и условиями работы проектируемой САУ, а также во многом определяется от интуиции практических навыков проектировщика. К этому относится также и выбор весовых коэффициентов.

Синтез оптимальных систем с помощью вариационного исчисления.

Задача Лагранжа

Эта задача на условный экстремум, и нас будет интересовать случай, когда условия представляют собой систему дифференциальных уравнений.