Оптимальные системы автоматического управления, страница 6

Если начальная точка и конечная точка  не фиксирована в пространстве X, а принадлежит начальному многообразию  размерности  и конечного многообразию  размерности , то к условиям теоремы необходимо добавить условие трансверсальности в начальных и конечных точках.

Сказано, что n-мерная вектор-функция  удовлетворяет условию трансверсальности в начальной или конечной точке траектории, если вектор  или  ортогональны касательной плоскости, проведенной к многообразию  в точке или к  в точке . Это иллюстрирует следующий рисунок:

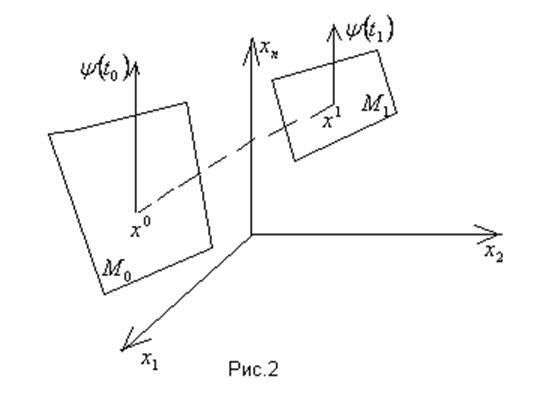
Таким образом, если концы траектории не фиксированы, то вектор-функции , помимо условий (1) и (2), должны также удовлетворять условиям трансверсальности. Условие трансверсальности позволяет определить  соотношений между координатами и .

Добавим к ним  соотношений.

Это все позволяет получить достаточную систему соотношений для решения задач оптимального управления.

Доказательство

Приведем доказательство теоремы для задач со свободным правым концом и фиксированным временем .

Пусть  - оптимальное управление,  - соответствующая ему траектория.

Рассмотрим малый интервал времени , где  и . Передадим управлению  приращение на промежутке , не изменяя значение управляющей функции вне этого интервала. Здесь не требуется, чтобы приращение , где , было малой величиной. Если управление ограничено неравенствами , то приращение удовлетворяет условию .

Такие вариации носят название игольчатыми вариациями.

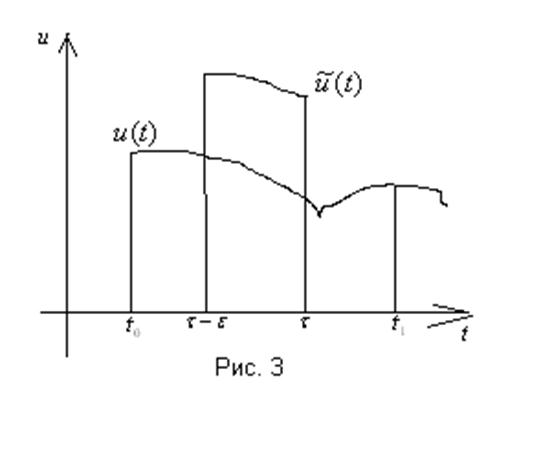
Найдем отклонение траектории системы, которое вызвано изменением управляющей функции:

 

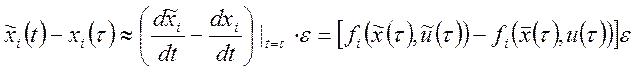
В силу непрерывности функции  разность  также имеет порядок малости , поэтому запишем:

  (13)

Из выражения (13) следует, что в момент времени  вариация имеет порядок малости . Здесь выражение (14) – это вариация координат системы:

     (14)

Согласно теореме о непрерывной зависимости от начальных условий, когда , вариации координат также будут иметь порядок малости . Теперь для траектории имеем  соответствующую систему уравнений:

 

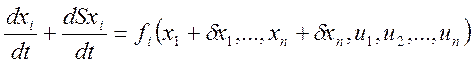
Теперь стандартный прием. Мы разложим правые части системы  в ряд Тейлора:

     (15)

Учитываем члены первого порядка малости.

Введем квадратичную матрицу размера  частных производных:

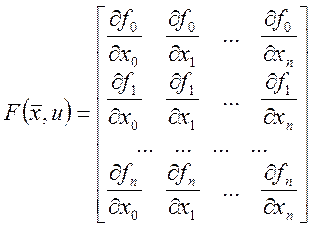
Теперь уравнение (15) запишем в векторной форме записи:

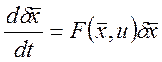  (16)

Введем в рассмотрение (n+1)-ый вектор , который удовлетворяет уравнению:

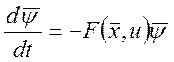   (17)

Это уравнение в координатной форме имеет вид:

   

Рассмотрим скалярное произведение . В силу того, что справедливо равенство:

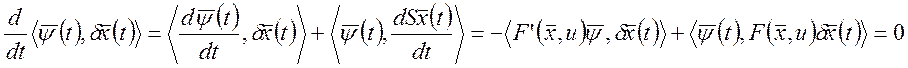
это скалярное произведение постоянно, когда .

Примем во внимание, что есть равенство . А по условию теорему управление доставляет заданному функционалу  минимум. Тогда, для управления, отличного от оптимального, будет справедливо неравенство:

Теперь зададимся граничными условиями на векторной функции :

  (18)

Тогда будет выполняться неравенство:

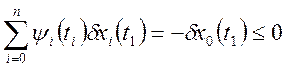
Учитывая, что:

 

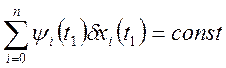
получаем:

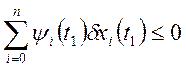
Подставляя в это неравенство выражение:

будем иметь:

Откуда получаем, с учетом :

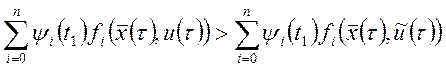
В качестве момента времени  можно выбрать любой момент из промежутка , поэтому окончательно можно записать:

где функция  определена равенством (8), а - это оптимальное управление. Необходимость теоремы 1 доказана.

Граничным условиям (18) соответствует ненулевое решение системы (17). Отметим, что граничные условия (18) вытекают из условия (2) теоремы и условия трансверсальности для свободного правого конца траектории.

Покажем, что принцип максимума позволяет из всех траекторий, которые начинаются в точке и проходящих через точку , выделить лишь отдельные изолированные траектории, удовлетворяющие необходимым условиям. Лишь эти оптимальные изолированные траектории и могут оказаться оптимальными, так как принцип максимума дает лишь необходимое условие оптимальности.

Всего в формулировке принципа максимума имеется 2n+2r независимых функций , ,  и столько же соотношений. То есть имеется полная система для определения этих переменных.

Действительно, уравнение (11) в условиях теоремы дает r соотношений между неизвестными функциями, если является внутренней точкой множества U, то для выполнения условия максимума необходимо обращение в нуль r частных производных:

  

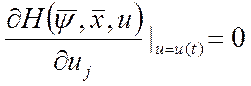
Если точка лежит на (r-1)-мерной грани области U, то есть одна из управляющих функций принимает предельное значение, то должно выполняться условие принадлежности точки этой грани, что дает одно соотношение, и для выполнения условия максимума функционала H должны обращаться в нуль ее частные производные, то есть производные функции  по всем параметрам этой грани (по всем остальным управлениям).

Помимо соотношений (11) мы имеем систему из 2n+2 уравнений (9) и (10). Таким образом из всего имеется 2n+2+r соотношений (9), (10), (11) для определения , , неизвестных.

Общее решение уравнений (9) и (10) содержит 2n+2 производных постоянных, но одна из них несуществующей, так как является линейной и однородной функцией переменных .

С учетом изложенного, решение системы (9), (10), (11) зависит от 2n параметров. Их нужно подобрать так, чтобы при   траектория  проходила через точку , а при  - через точку , то есть через прямую П. Число также является параметром. Всего имеем 2n+1 параметров, которые подлежат определению.

Условие прохождения траектории через точку и прямую П дает 2n+1 условий, поэтому можно ожидать, что имеются отдельные изолированные траектории соединяющие точкус прямой П и удовлетворяющие требованиям теоремы принципа максимума. Если в частности условиям теоремы удовлетворяет единственная траектория, а из физических соображений ясно что оптимальная траектория существует, то найденная траектория будет оптимальной.