Имеется функционал:
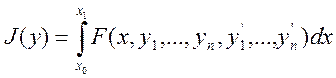 (1)
(1)
При этом допустимые кривые ![]() , среди которых ищется экстремум
функционала, должны удовлетворять граничным условиям:
, среди которых ищется экстремум
функционала, должны удовлетворять граничным условиям:
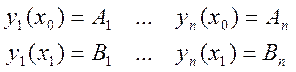 (2)
(2)
И условиям вида:
![]()
![]() (3)
(3)
При этом ![]() .
Мы предполагаем, что условия (3) являются независимыми, а это значит, что для
всех
.
Мы предполагаем, что условия (3) являются независимыми, а это значит, что для
всех ![]() , которые удовлетворяют условиям (3),
справедливо:
, которые удовлетворяют условиям (3),
справедливо:
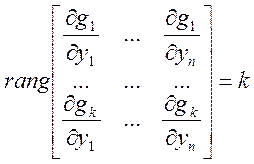
Таким образом, функционал (1)
рассматривается не на всех допустимых кривых, удовлетворяющих граничным
условиям (2), а только на тех кривых, которые удовлетворяют системе уравнений
(3). Важно, чтобы условия (2) и (3) были согласованными, то есть начальные и
конечные точки должны удовлетворять ![]() - мерному
многообразию, которая задается системой уравнений (3).
- мерному
многообразию, которая задается системой уравнений (3).
Следует отметить, что граничные условия можно задать следующим образом:
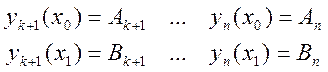
А недостающее условие определяется из уравнений связи (3).
Это задача на условный экстремум
называется задачей Лагранжа с голономными связями ![]() .
.
Введем в рассмотрение новый функционал:
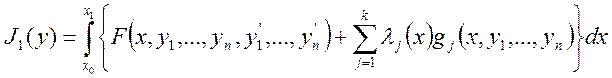 (4)
(4)
Здесь ![]() -
функции, подлежащие определению.
-
функции, подлежащие определению.
Относительно функционала (4)
решается задача на безусловный экстремум, при чем подлежащие определению
функции ![]() и
и ![]() .
Система уравнений Эйлера-Лагранжа для функционала (4) принимает вид:
.
Система уравнений Эйлера-Лагранжа для функционала (4) принимает вид:
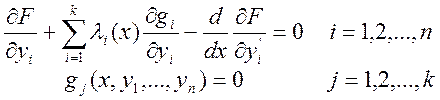 (5)
(5)
Система (5) состоит из ![]() уравнений, которые совпадают с
числом искомых функций
уравнений, которые совпадают с
числом искомых функций ![]() и
и ![]() .
Общее решение системы (5) содержит
.
Общее решение системы (5) содержит ![]() произвольных
постоянных, для определения которых используются граничные условия (2).
произвольных
постоянных, для определения которых используются граничные условия (2).
Если кривая ![]() доставляет безусловный экстремум
функционалу (4), то на ней достигается и условный экстремум функционала (1). В
самом деле, если на кривой
доставляет безусловный экстремум
функционалу (4), то на ней достигается и условный экстремум функционала (1). В
самом деле, если на кривой ![]() достигается
безусловный экстремум функционала (4), то эта кривая доставляет экстремум
функционалу (5).
достигается
безусловный экстремум функционала (4), то эта кривая доставляет экстремум
функционалу (5).
Тогда ![]() ,
и если кривая
,
и если кривая ![]() доставляет безусловный
экстремум функционалу
доставляет безусловный
экстремум функционалу ![]() , то, в частности, она
будет доставлять экстремум и в более узком классе кривых, удовлетворяющих
уравнениям связи.
, то, в частности, она
будет доставлять экстремум и в более узком классе кривых, удовлетворяющих
уравнениям связи.
Докажем следующую теорему:
Теорема 1
Если функция ![]() доставляет экстремум функционалу (1)
и удовлетворяет условиям связи (3), то существуют такие множители
доставляет экстремум функционалу (1)
и удовлетворяет условиям связи (3), то существуют такие множители ![]() , что функция
, что функция ![]() удовлетворяет
уравнениям Эйлера-Лагранжа для функционала (4).
удовлетворяет
уравнениям Эйлера-Лагранжа для функционала (4).
Доказательство
Первая вариация функционала (1):
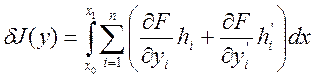
Здесь ![]() .
Это допустимые приращения функции
.
Это допустимые приращения функции ![]() , удовлетворяющей
граничным условиям:
, удовлетворяющей
граничным условиям:
![]()
Интегрируя по частям выражение
для первой вариации и учитывая граничные условия для переменной ![]() , будем иметь:
, будем иметь:
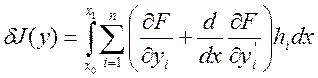
Функции ![]() удовлетворяют
уравнениям связи, поэтому приращение
удовлетворяют
уравнениям связи, поэтому приращение ![]() не является
независимым, и применять лемму Лагранжа для определения необходимого условия
экстремума нельзя.
не является
независимым, и применять лемму Лагранжа для определения необходимого условия
экстремума нельзя.
Для определения зависимости между
приращениями ![]() разложим левую часть равенств:
разложим левую часть равенств:
![]()
в ряд Тейлора, ограничившись
членами первого порядка малости относительно ![]() .
.
Учитывая, что:
![]()
получаем:
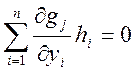
![]() (6)
(6)
Эти равенства представляют собой
систему линейных однородных алгебраических уравнений относительно ![]() . По условию, ранг матрицы
. По условию, ранг матрицы 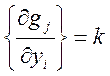 .
.
Поэтому, можно выделить ![]() свободных неизвестных
свободных неизвестных ![]() . Это независимые, в отличие от
основных неизвестных
. Это независимые, в отличие от
основных неизвестных ![]() , которые при решении системы
(6) выражаются через свободные неизвестные
, которые при решении системы
(6) выражаются через свободные неизвестные ![]() .
Умножим почленно каждое уравнение системы (6) на
.
Умножим почленно каждое уравнение системы (6) на ![]() ,
проинтегрируем по
,
проинтегрируем по ![]() в пределах от
в пределах от ![]() до
до ![]() и
сложим полученное равенство с выражением для вариации функционала
и
сложим полученное равенство с выражением для вариации функционала ![]() .
.
Принимая во внимание необходимое условие экстремума:
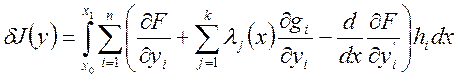
Выделим ![]() так,
чтобы первые
так,
чтобы первые ![]() слагаемых в подынтегральной сумме
обратились в нуль:
слагаемых в подынтегральной сумме
обратились в нуль:
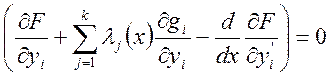
![]() (7)
(7)
Равенство (7) можно рассматривать
как систему линейных алгебраических уравнений относительно ![]() . Определитель системы
. Определитель системы ![]() по предположению отличен от нуля.
Поэтому система
по предположению отличен от нуля.
Поэтому система ![]() имеет единственное
решение.
имеет единственное
решение.
При таком выборе ![]() необходимо условие экстремума
принимает вид:
необходимо условие экстремума
принимает вид:
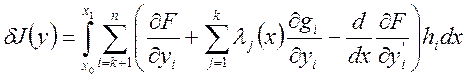
Здесь ![]() будут
независимыми. Поэтому в силу леммы Лагранжа:
будут
независимыми. Поэтому в силу леммы Лагранжа:
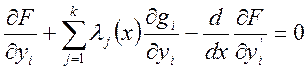
![]() (8)
(8)
Из уравнений (7) и (8) следует,
что функции ![]() , доставляющие экстремум функционалу
(1) удовлетворяют уравнениям Эйлера-Лагранжа для вспомогательного функционала
(4).
, доставляющие экстремум функционалу
(1) удовлетворяют уравнениям Эйлера-Лагранжа для вспомогательного функционала
(4).
Задача Чаплыгина
Определить замкнутую кривую, по
которой должен двигаться центр масс летательного аппарата, чтобы за время ![]() облететь наибольшую площадь, если
задана постоянная скорость ветра
облететь наибольшую площадь, если
задана постоянная скорость ветра ![]() . Скорость
летательного аппарата постоянна и равна
. Скорость
летательного аппарата постоянна и равна ![]() .
Все выше сказанное иллюстрируется рисунком:
.
Все выше сказанное иллюстрируется рисунком:
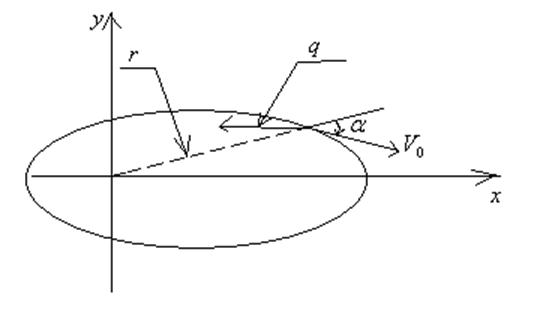
При решении задачи требуется определить максимум для функционала:
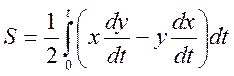 (1)
(1)
при наличии связей:
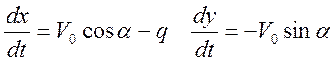 (2)
(2)
Решение
Составим вспомогательный функционал:
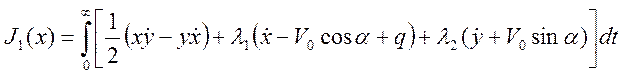
Теперь запишем уравнения Эйлера-Лагранжа:
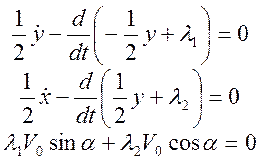 (3)
(3)
Интегрируя первые 2 уравнения (3) находим:
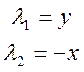 (4)
(4)
Постоянные интегрирования равны нулю за счет переноса оси координат.
Найденные значения ![]() и
и ![]() подставим
во второе уравнение (3):
подставим
во второе уравнение (3):
![]()
Из последнего уравнения следует, что можно ввести следующие обозначения:
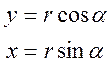
И тогда получим:
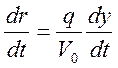 (5)
(5)
Теперь проинтегрируем это уравнение и получим:
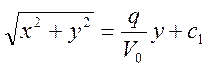 (6)
(6)
Уравнение (6) представляет собой уравнение эллипса, которое можно привести к следующему виду:
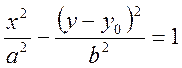
Здесь малая полуось определяется следующим образом:
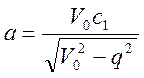
Большая полуось:
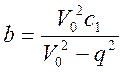
Смещение центра эллипса:
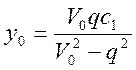
Расстояние от центра эллипса до фокуса определяется следующим образом:
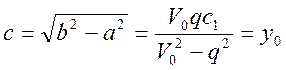
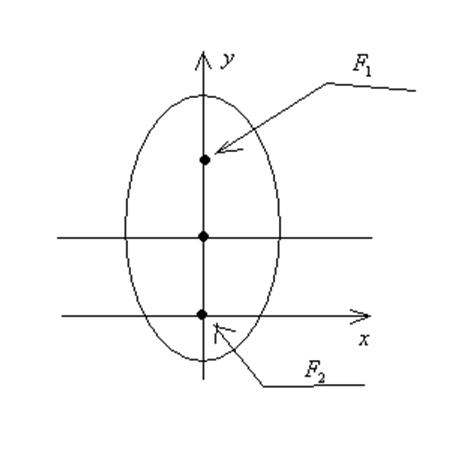
Таким образом, искомая траектория представляет собой эллипс, один из фокусов которого расположен в начале координат, а большая ось перпендикулярна направлению ветра.
При этом эксцентриситет эллипса:
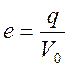
Все это показано на рисунке:
Постоянная интегрирования ![]() определяется временем полета
определяется временем полета ![]() .
.
Изопериметрическая задача
Это задача на условный экстремум.
Формулировка: Среди всех гладких кривых, которые удовлетворяют граничным условиям и условиям:
![]()
![]()
![]()
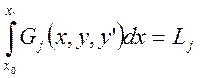
Требуется определить кривую, на которой достигается экстремум функционала:
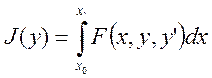
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.