Анализ и синтез линейных систем автоматического регулирования

Министерство образования РФ

Сибирский государственный  технологический

                                           университет

Факультет АиИТ

Кафедра АПП

Анализ  и синтез линейных систем автоматического

регулирования

Пояснительная записка

(АПП.000000.006.ПЗ)

Выполнил: студент группы 22-2 КУПЦОВ А.А.

Проверил: преп-ль

ЧМЫХ Г.И.

Задание к расчёту

а) Преобразовать структурную схему (рис.1.1) и определить передаточные функции разомкнутой и замкнутой системы.

б) Исследовать систему на устойчивость.

 Исходные данные

Структурная схема АСР, состоящая из типовых динамических звеньев (рис.1.1).                   

Числовые данные:

коэффициенты усиления: К₁ = 0.11, К₂ = 360, К₃ = 2.4, К₄ = 4.7;

постоянные времени: T₃ = 0.94, T₄ = 0.072, T₅ = 0.062;

Показатели качества:

время регулирования: t_p = 1,6 с;

перерегулирование s = 25%.

Корректирующее устройство включено в схему последовательно.

АСР работает по задающему воздействию.

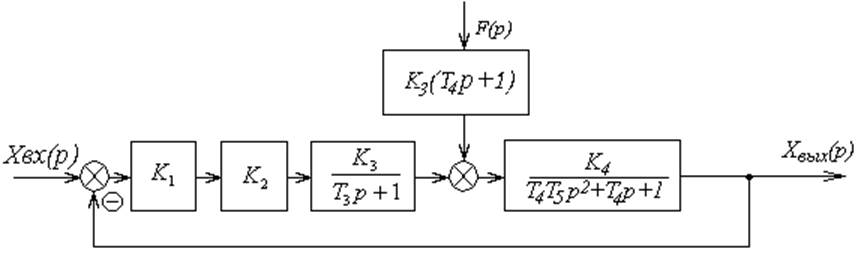
Структурная схема

 Рекомендуемая литература

  А. А. Воронов Теория автоматического управления // 2-е изд., перераб, и доп. –М: «Высшая школа», 1986 – 504 с.

  М. И. Захаров В. А. Дорошенко  Анализ и синтез систем автоматического регулирования // методические указания.

Руководитель: _________________

(подпись)

Задание принял

к исполнению: __________________

(подпись)

Содержание

1. Введение ………………………………………………………………………………………………

2.Расчётная часть …………………………………………………………………………………….

2.1. Преобразование структурной схемы …………………………………………………………

2.2. Исследование на устойчивость ………………………………………………………………..

2.2.1. Критерий Гурвица …………………………………………………………………………

2.2.2. Критерий Рауса ……………………………………………………………………………

2.2.3. Критерий Михайлова ……………………………………………………………………..

2.2.4. Критерий Найквиста ……………………………………………………………………..

2.2.5. Логарифмический критерий …………………………………………………………….

 2. Расчётная часть

2.1. Преобразование структурной схемы.

На систему автоматического регулирования действует задающее и возмущающее воздействия (рис.1.1). Для системы, работающей по задающему воздействию, F(р) равна нулю, следовательно, структурная схема имеет следующий вид:

Рис.2.1. Эквивалентная схема

1. Находим передаточную функцию для разомкнутой цепи:

  Wр(p) =W₁(p)W₂(p)W₃(p)W₅(p),                                      (2.1)

.

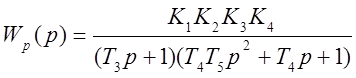Подставим числовые значения в выражение (2.1):

.

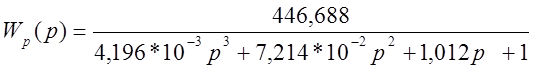2. Находим передаточную функцию для замкнутой цепи с обратной единичной связью:

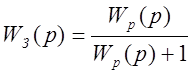.                                                          (2.2)

Подставим числовые значения в выражение (2.2):

.

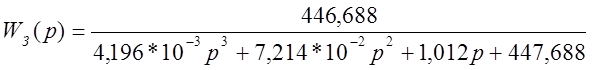2.2. Исследование на устойчивость

2.2.1. Критерий Гурвица

Чтобы система была устойчивой необходимо и достаточно, чтоб главный определитель матрицы Гурвица и все его диагональные миноры были не отрицательны.

   Критерий Гурвица предполагает исследование замкнутой системы по ее характеристическому многочлену:

4,196*10^-3P³+ 7,214*10^-2P²+1,012Р+447,688 = 0.

По коэффициентам этого многочлена составляем квадратную матрицу следующего вида: 

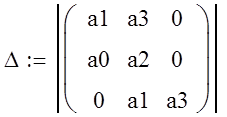                                                (2.3)

Найдём главный и диагональные миноры:

,

,

,

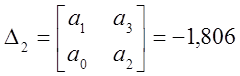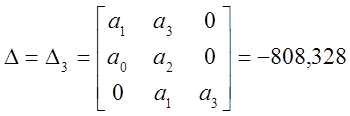Вывод: Данная система в замкнутом состоянии является не устойчивой, т.к. несколько определителей матрицы меньше нуля.

2.2.2.  Критерий Рауса

 Для определения устойчивости системы по коэффициентам характеристического уравнения замкнутой системы, Раус предложил правило оформленное в виде таблицы:  

    Таблица 2.1.- Таблица Рауса

а0	а2	а4	а6
а1	а3	а5	a7
a1a2-a0a3  b1=        a1	а1a4-a0a5 b2=       a1	a1a6-a0a7 b3=     a1	а1a8-a0a9 b4=     a1	××××
b1a3-a1b2 c1=        b1	b1a5-a1b3 c2=    b1	b1a7-a1b4 c3=     b1	b1a9-a1b5 c4=     b1	××××
c1b2-b1c2 d1=         c1	с1b3-b1c3 d2=     c1	c1b4-b1c4 d3=      c1	c1b5-b1c5 d4=     c1	××××
×××	×××	×××	×××	××××

Выписываем характеристический многочлен и вычисляем коэффициенты таблицы

Рауса:

4,196*10^-3P³+ 7,214*10^-2P²+1,012Р+447,688 = 0.

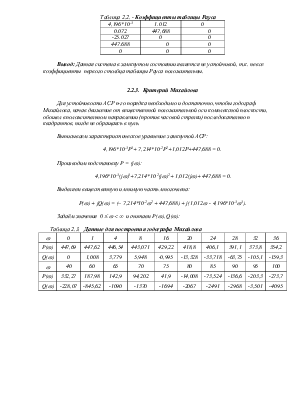
Таблица 2.2. - Коэффициенты таблицы Рауса

4,196*10-3	1.012	0
0.072	447,688	0
-25.027	0	0
447.688	0	0
0	0	0

Вывод: Данная система в замкнутом состоянии является не устойчивой, т.к. не все коэффициенты  первого столбца таблицы Рауса положительны.

2.2.3.  Критерий Михайлова

Для устойчивости АСР n-го порядка необходимо и достаточно, чтобы годограф Михайлова, начав движение от вещественной положительной оси комплексной плоскости, обошел в положительном направлении (против часовой стрелки) последовательно n квадрантов, нигде не обращаясь в нуль.

Выписываем характеристическое уравнение замкнутой АСР:

4,196*10^-3P³+ 7,214*10^-2P²+1,012Р+447,688 = 0.

Производим подстановку P = (jw):

 4,196*10^-3(jw)³+7,214*10^-2(jw)²+ 1,012(jw)+ 447,688 = 0.

Выделяем вещественную и мнимую часть многочлена:

P(w) + jQ(w) = (– 7,214*10^-2w² + 447,688) + j(1,012w  - 4,196*10^-3w³).

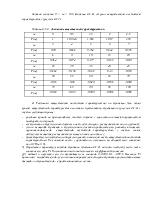
Задаём значения  0 £w<¥  и считаем P(w), Q(w):

Таблица 2.3.   Данные для построения годографа Михайлова

w	0	1	4	8	16	20	24	28	32	36
P(w)	447,69	447,62	446,54	443,071	429,22	418,8	406,1	391,1	373,8	354,2
Q(w)	0	1,008	3,779	5,948	-0,995	-13,328	-33,718	-63,75	-105,1	-159,3
w	40	60	65	70	75	80	85	90	95	100
P(w)	332,27	187,98	142,9	94,202	41,9	-14,008	-73,524	-136,6	-203,3	-273,7
Q(w)	-228,07	-845,62	-1090	-1370	-1694	-2067	-2491	-2968	-3,501	-4095

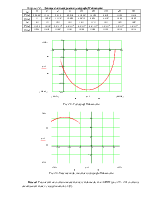
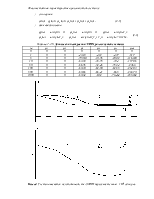
По данным (табл.2.3) строим годограф Михайлова (рис.2.2).

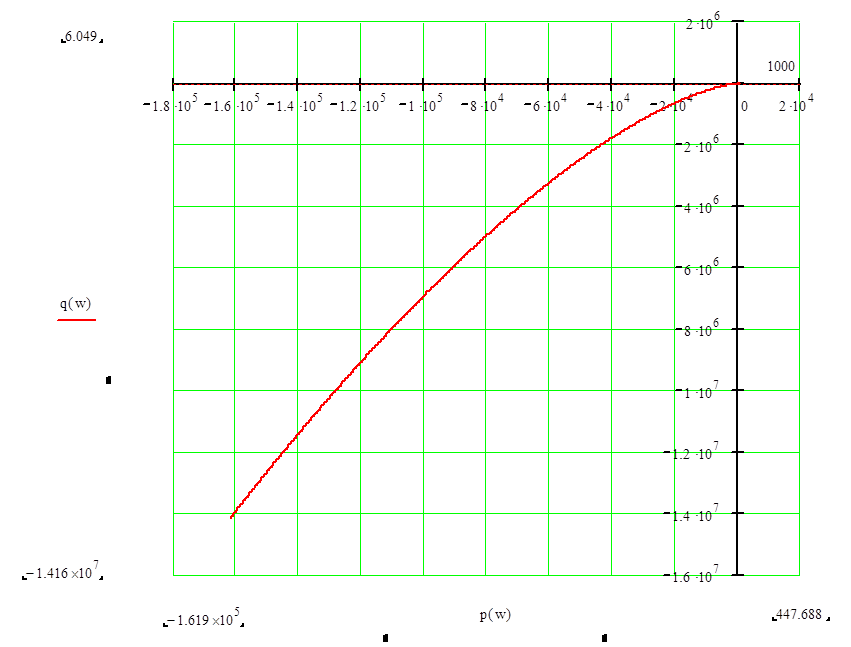
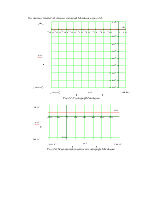
Рис.2.2. Г одограф Михайлова

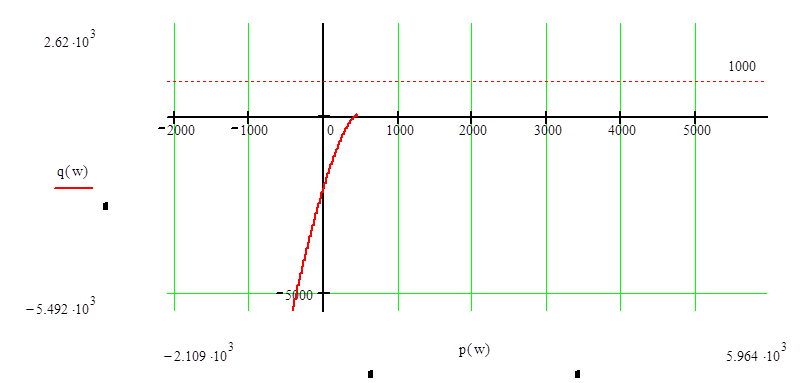
Рис.2.3. Увеличенный участок на годографе Михайлова

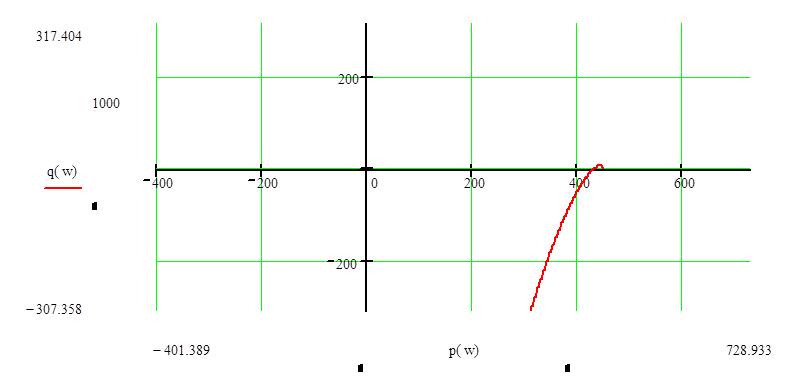
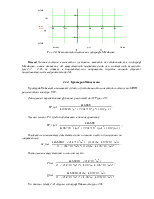
Рис.2.4. Увеличенный участок на годографе Михайлова

Вывод: Данная система в замкнутом состоянии  является не устойчивой, т.к. годограф Михайлова, начав движение от вещественной положительной оси комплексной плоскости (рис.2.2 – 2.4), не обошел в положительном направлении (против часовой стрелки) последовательно 3 квадранта (табл.2.3).