Анализ и синтез линейных систем автоматического регулирования, страница 3

Проводим прямые с ординатами Lм и - Lм (пунктирными линиями на рисунок (3.1.1). Затем после построения среднечастотной асимптоты (наклон –20 дб/дек) наносим сопрягающую асимптоту с наклоном –40 дб/дек, начиная её из точки среднечастотной асимптоты с ординатой Lм = 16,5 дб.

Высокочастотная асимптота желаемой ЛАЧХ мало влияет на свойства системы, поэтому выбираем (наклон –40 дб/дек) её так, чтобы корректирующее устройство было возможно более простым. Это достигается при совмещении высокочастотных асимптот характеристик Lж(w) и L₀(w).

3.1.2 Определение передаточной функции желаемой ЛАЧХ

По виду желаемой ЛАЧХ Lж(w) составляем передаточную функцию разомкнутой скорректированной системы:

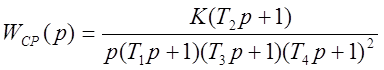.                               (3.1.3)

Проверяем избыток фазы при контрольных частотах w_а = 1,148 с^-1 w_СР = 6,552 с^-1 и

w_b  47,619 с^-1 (рис.2.1.1) по следующей формуле:

g = 180⁰ + j,                                                  (3.1.4)

где 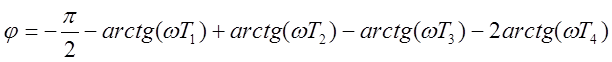, j < 0.            (3.1.5)

Основная задача сводится к нахождению коэффициентов времени Т₁, Т₂, Т₃, Т₄ по формуле:

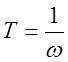.                                                        (3.1.6)

 Запас устойчивости по фазе в соответствующих точках должен как можно меньше отличаться от значения g = 48⁰, найденного по номограмме ([1], страница 273). Допустимо отклонение

g± (6⁰¸7⁰). В целях достижения этого условия рекомендуется передвигать сопрягающиеся асимптоты w_а и w_b(w_а – частота сопряжения среднечастотного и низкочастотного участков, w_b - частота сопряжения среднечастотного и высокочастотного участков) так, чтобы ординаты L₁(w_а) и L₂(w_b) менялись не более 10% от их первоначального значения (в данном случае допустимо ±1,65 дб).

 Сопрягающие частоты и соответствующие им постоянные времени, полученные из выражения (3.1.5) приведены в таблице 3.1.1.

Таблица 3.1.1

Таблица 3.1.2 – Проверка избытка фазы при контрольных частотах

wа = 1,148 с-1	L1(wа) = 15 дб	jа = -125,66080	gа =54,33920	gа =480 + 6,33920
wb =  47,619 с-1	L2(wb) = -16,5 дб	jb = -162,52580	gb =17,47420	gb =480 – 31,47420
wСР =  6,552 с-1	jСР = -162,52580		gс =70,87960	gс =480 + 22,87960

После соответствующих преобразований передаточная функция желаемой ЛАЧХ разомкнутой скорректированной системы принимает следующий вид:

.

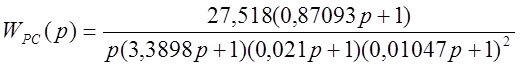3.1.3 Расчет переходного процесса по вещественной частотной

характеристике методом трапеций

Наиболее известным методом определения переходных процессов является метод построения кривой переходного процесса с помощью трапецеидальных вещественных частотных характеристик АСР.

1) Записываем передаточную функцию замкнутой системы на основе передаточной функции скорректированной разомкнутой системы (системы с включением в ее структуру корректирующего устройства)

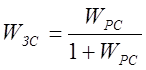,                                               (3.1.7)

.

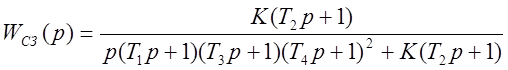2) Вычисляем коэффициенты этой передаточной функции:

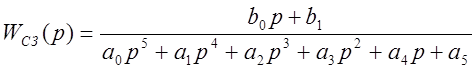,                       (3.1.8)

где ;

;

;

;

;

;

;

.

Передаточная функция скорректированной замкнутой системы с учётом найденных коэффициентов имеет следующий вид:

.

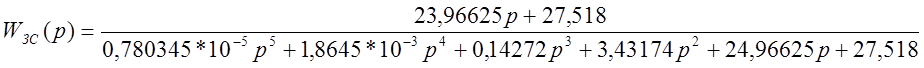3) Выделяем вещественную частотную характеристику замкнутой системы, произведя следующую подстановку:

,                                                         (3.1.9)

.

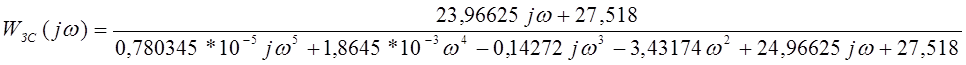Записываем значения вещественной и мнимой части для полиномов числителя и знаменателя частотной передаточной функции замкнутой АСР:

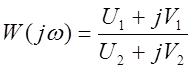,                                                   (3.1.10)

где ;

;

;

.

Записываем значение вещественной частотной характеристики для замкнутой системы:

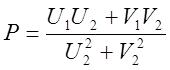 ,                                                      (3.1.11)

.

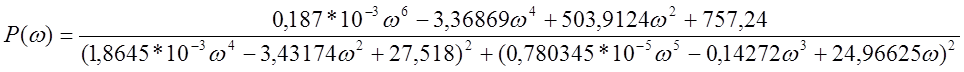Задавая значения 0 < w < 100 (таблица 3.1.3), строим вещественную частотную характеристику (рисунок 3.1.2).

Таблица 3.1.3 – Значения вещественной характеристики

w	0	0,5	1,5	2	2,5
Р(w)	1	1,01946	1,065	1,057	1,03
w	3	4	5	6	7
Р(w)	0,99	0,888	0,764	0,634	0,505
w	8	9	10	15	20
Р(w)	0,384	0,274	0,177	-0,125	-0,219
w	25	30	35	40	45
Р(w)	-0,224	-0,196	-0,162	-0,13	-0,103
w	50	55	60	65	70
Р(w)	-0,08	-0,06	-0,049	-0,038	-0,029
w	75	85	90	95	100
Р(w)	-0,022	-0,013	-0,009	-0,008	-0,005

4) Разбиваем вещественную частотную характеристику на трапеции. Для этого кривую вещественной характеристики заменяем приближенно трапециями (рисунок 3.1.3) с учетом следующих правил:

-  разбивка кривой на прямолинейные участки должна с возможно меньшей погрешностью повторять ход кривой;

-  все трапеции и треугольники должны иметь одну сторону, расположенную на оси ординат;

-  сумма площадей трапеций и треугольников должна приблизительно равняться площади, ограниченной кривой       вещественной частотной характеристики с учетом знаков отдельных площадок расположенных выше и ниже оси абсцисс;

-  более тщательно необходимо аппроксимировать начальную часть вещественной частотной характеристики. Ее конечную часть с ординатами, меньшими по абсолютному значению, чем 0.1Р(w = 0).